广东省深圳育才教育集团2023-2024学年七年级下学期数学期中考试试卷

试卷更新日期：2024-04-26 类型：期中考试

进入出卷网下载

一、nbsp;．选择题（共10小题，每小题3分，共计30分）

1. 下列运算正确的是（）

A、 $3 a + 2 a = 5 a^{2}$ B、 $3 a^{3} · 2 a^{2} = 6 a^{6}$ C、 ${(- 2 a)}^{3} = - 6 a^{3}$ D、 $a^{6} \div a^{5} = a$

查看试题解析
2. 如图，在三角形 $A B C$ 中， $∠ C = 90 °$ ， $A C = 5$ ，点 P是边 $B C$ 上动点，则 $A P$ 的长不可能是（）

A、4.8 B、5 C、6 D、7

查看试题解析
3. 司机王师傅到加油站加油，如图是所用的加油机上的数据显示牌，其中的常量是（）

A、金额 B、数量 C、单价 D、金额和数量

查看试题解析
4. 华为Mate40pro手机搭载麒麟9000处理器，这是手机行业首批采用5nm工艺制式芯片，1nm=0.000 000 001m，那么5nm用科学记数法表示为（）

A、 $5 \times 1 0^{9} m$ B、 $5 \times 1 0^{- 10} m$ C、 $5 \times 1 0^{- 8} m$ D、 $5 \times 1 0^{- 9} m$

查看试题解析
5. 为了测试一种皮球的弹跳高度与下落高度之间的关系，通过试验得到下列一组数据（单位：厘米）：
下落高度
40
50
80
100
150
弹跳高度
20
25
40
50
75
在这个问题中，如果该皮球的下落高度为180厘米，估计相对应的弹跳高度为（）

A、90厘米 B、85厘米 C、80厘米 D、100厘米

查看试题解析
6. 一个长方形的面积为4a²-6ab+2a ，若它的一边长为2a ，则它的周长为( )

A、4a-3b B、8a-6b C、4a-3b+1 D、8a-6b+2

查看试题解析
7. 直尺与三角尺按如图所示的方式叠放在一起，在图中所标记的角中，与 $∠ 1$ 互余的角有( )
A 2个

A、3个 B、4个 C、5个

查看试题解析
8. 如图，将水以匀速（即单位时间内注入水的体积相同）注入下面圆柱体的容器中，请找出容器内水的高度h和时间t变化关系的图象（）

A、 B、 C、 D、

查看试题解析
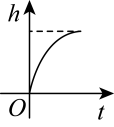9. 如图，下列推理错误的是（）

A、若 $∠ B = ∠ 3$ ，则 $A B ∥ C D$ B、若 $∠ B = ∠ D$ ，则 $A B ∥ C D$ C、若 $∠ 3 = ∠ D$ ，则 $B E ∥ D F$ D、若 $∠ 1 = ∠ D$ ，则 $B E ∥ D F$

查看试题解析
10. 某种细菌每分钟可由1个分裂成2个，将1个细菌放在培养瓶中经过64分钟就能分裂满一瓶．若将4个这种细菌放入同一个培养瓶中，分裂满一瓶的时间是（　　）

A、16分钟 B、32分钟 C、52分钟 D、62分钟

查看试题解析

二、nbsp;．填空题（共5小题，每小题3分，共计30分）

11. 一个老人非常喜欢孩子，每当有孩子到他家做客时，老人都要拿出糖果招待他们．如果来1个孩子，老人就给孩子1块糖果；来2个孩子，老人就给每个孩子2块糖果；如果来3个孩子，老人就给每个孩子3块糖果；……，．有一天， $x$ 个孩子一起去看老人，第二天，有 $y$ 个孩子一起去看老人，第三天 $(x + y)$ 个孩子一起去看老人，那么，第三天老人给出去的糖果比前两天给出去的糖果多块.

查看试题解析
12. 如图，用一段长为 $60 m$ 的篱笆围成一个一边靠墙（墙的长度不限）的长方形菜园 $A B C D$ ，设与墙平行的篱笆 $A B$ 的长为 $x m$ ，菜园的面积为 $y m^{2}$ ．试写出 $y$ 与 $x$ 之间的关系式．

查看试题解析
13. 一个角是它的补角的五分之一，则这个角的余角是度．

查看试题解析
14. 用如图所示正方形和长方形卡片若干张，拼成一个边长为a＋3b的正方形，需要B类卡片张．

查看试题解析
15. 如图，在长方形 $A B C D$ 中， $A B = 6$ ，点E ， F是边 $B C$ ， $C D$ 上的点， $E C = 3$ ，且 $B E = D F = x$ ，分别以 $F C$ ， $C B$ 为边在长方形 $A B C D$ 外侧作正方形 $C F G H$ 和 $C B M N$ ，若长方形 $C B Q F$ 的面积为20，则图中阴影部分的面积和为

查看试题解析

三、nbsp;．解答题（共7大题，其中第16题8分、第17题6分、第18题6分、第19题9分、第20题8分，第21题9分、第22题9分，共计55分）

16. 计算：

(1)、 $1 {(π - 4)}^{0} + {(\frac{1}{4})}^{- 2} + {(\frac{1}{2})}^{2023} \times 2^{2025}$

(2)、 $20 1^{2} - 198 \times 202$ （用整式乘法公式计算）．

查看试题解析
17. 已知 $x^{2} - 2 x - 1 = 0$ ，求代数式 $2 (x + 1) (x - 1) - {(x + 1)}^{2}$ 的值．

查看试题解析
18. 如图，点D是∠ABC内部一点，DE//AB交BC于点E．

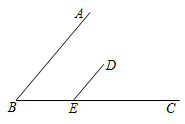(1)、请尺规作图：画出射线DF，使得DF//BC，交直线AB于点F；

(2)、请你直接写出∠B与∠EDF的数量关系：

查看试题解析

19. 如图，一扇窗户，窗框为铝合金材料，上面是由三个大小相等的扇形组成的半圆窗框构成，下面是由两个大小相等的长

x

，宽

y

的长方形窗框构成，窗户全部安装玻璃．（本题中

π

取

3

，长度单位为米）

	铝合金（元/米）	玻璃（元/平方米）
甲厂商	$180$	不超过 $100$ 平方米的部分， $90$ 元/平方米，超过 $100$ 平方米的部分， $70$ 元/平方米
乙厂商	$200$	$80$ 元/平方米，每购一平方米玻璃送 $0.1$ 米铝合金

(1)、一扇这样窗户一共需要铝合金多少米？（用含

x ， y

的式子表示）

(2)、一扇这样窗户一共需要玻璃多少平方米？铝合金窗框宽度忽略不计（用含

x ， y

的式子表示）

(3)、某公司需要购进

10

扇这样的窗户，在同等质量的前提下，甲、乙两个厂商分别给出如表中报价，当

x = 4 ， y = 2

时，该公司在哪家厂商购买窗户合算？

查看试题解析

20. 小明从家出发骑自行车去上学，当他以往常的速度骑了一段路后，突然想起要买文具，于是又折回到刚经过的文具店，买到文具后继续骑车去学校．如图是他本次上学所用的时间与离家的距离之间的关系图，根据图中提供的信息回答下列问题：

(1)、小明家到学校的距离是米，文具店到学校的距离是米；

(2)、小明在文具店停留了分钟，本次上学途中，小明一共行驶了米；

(3)、观察图象，请编制一道新的问题并给出解答过程．

查看试题解析
21. 如图1，直线 $A B ∥ C D$ ，另一直线 $E F ⊥ A B$ 分别交AB、CD于M、N ，将射线MA绕点M以每秒2°的速度逆时针旋转到 $M A^{'}$ ，同时射线NC绕点N以每秒3°的速度顺时针旋转到 $N C^{'}$ ，旋转的时间为t（ $0 < t < 60$ ）秒．

(1)、如图2，当 $t = 12$ 秒时，射线 $M A^{'}$ 与 $N C^{'}$ 相交于点P ，求 $∠ M P N$ 的度数；

(2)、如图3，当射线 $M A^{'}$ 与 $N C^{'}$ 平行时，求t的值；

(3)、当射线 $M A^{'}$ 与 $N C^{'}$ 互相垂直时，求t的值．

查看试题解析
22. 多项式乘法的学习中，等式 $(a + b) (c + d) = a c + a d + b c + b d$ 可以用平面图形（图 $1$ ）的面积来说明．

(1)、【初步探究】
请使用（图 $2$ ）的 $2$ 种规格的正方形，设计一个平面图形方案说明等式 ${(a + b)}^{2} = a^{2} + 2 a b + b^{2}$ 是正确的；

(2)、【知识拓展】
为进一步探索部分平面图形的面积与等式的关系，在某次数学活动中，准备（图 $3$ ）所示的三种规格的正方形、长方形卡片若干张．小明从中选取 $9$ 张，拼成一个边长为 $(a + b + c)$ 的正方形，请你写出与其面积相应的等式；

(3)、【延伸应用】
请利用（ $2$ ）中得到的等式解答以下问题：若实数 $x ， y$ ，满足 $x^{2} + 4 y^{2} + 9 z^{2} = 8$ ， $x + 2 y + 3 z = 4$ ，求 $2 x y + 3 x z + 6 y z$ 的值．

查看试题解析

下落高度	40	50	80	100	150
弹跳高度	20	25	40	50	75

广东省深圳育才教育集团2023-2024学年七年级下学期数学期中考试试卷

一、nbsp;．选择题（共10小题，每小题3分，共计30分）

二、nbsp;．填空题（共5小题，每小题3分，共计30分）

三、nbsp;． 解答题（共7大题，其中第16题8分、第17题6分、第18题6分、第19题9分、第20题8分，第21题9分、第22题9分，共计55分）

三、nbsp;．解答题（共7大题，其中第16题8分、第17题6分、第18题6分、第19题9分、第20题8分，第21题9分、第22题9分，共计55分）