湖北省武汉市江汉区2024年中考数学一模试卷

试卷更新日期：2024-04-26 类型：中考模拟

进入出卷网下载

一、选择题（共10小题，每小题3分，共30分）

1. 2024的相反数是（　　）

A、2024 B、﹣2024 C、 $\frac{1}{2024}$ D、 $- \frac{1}{2024}$

查看试题解析
2. 在一些美术字中，有的汉字是轴对称图形．下面4个汉字中，可以看作是轴对称图形的是（　　）

A、 B、 C、 D、

查看试题解析
3. 掷两枚质地均匀的骰子，下列事件是随机事件的是（）

A、点数的和为1 B、点数的和为6 C、点数的和大于12 D、点数的和小于13

查看试题解析
4. 下列计算 ${(3 a^{3})}^{2}$ 正确的是（）

A、 $3 a^{6}$ B、 $6 a^{5}$ C、 $8 a^{9}$ D、 $9 a^{6}$

查看试题解析
5. 如图是由3个相同的小正方体搭成的几何体，那么这个几何体的俯视图是（）

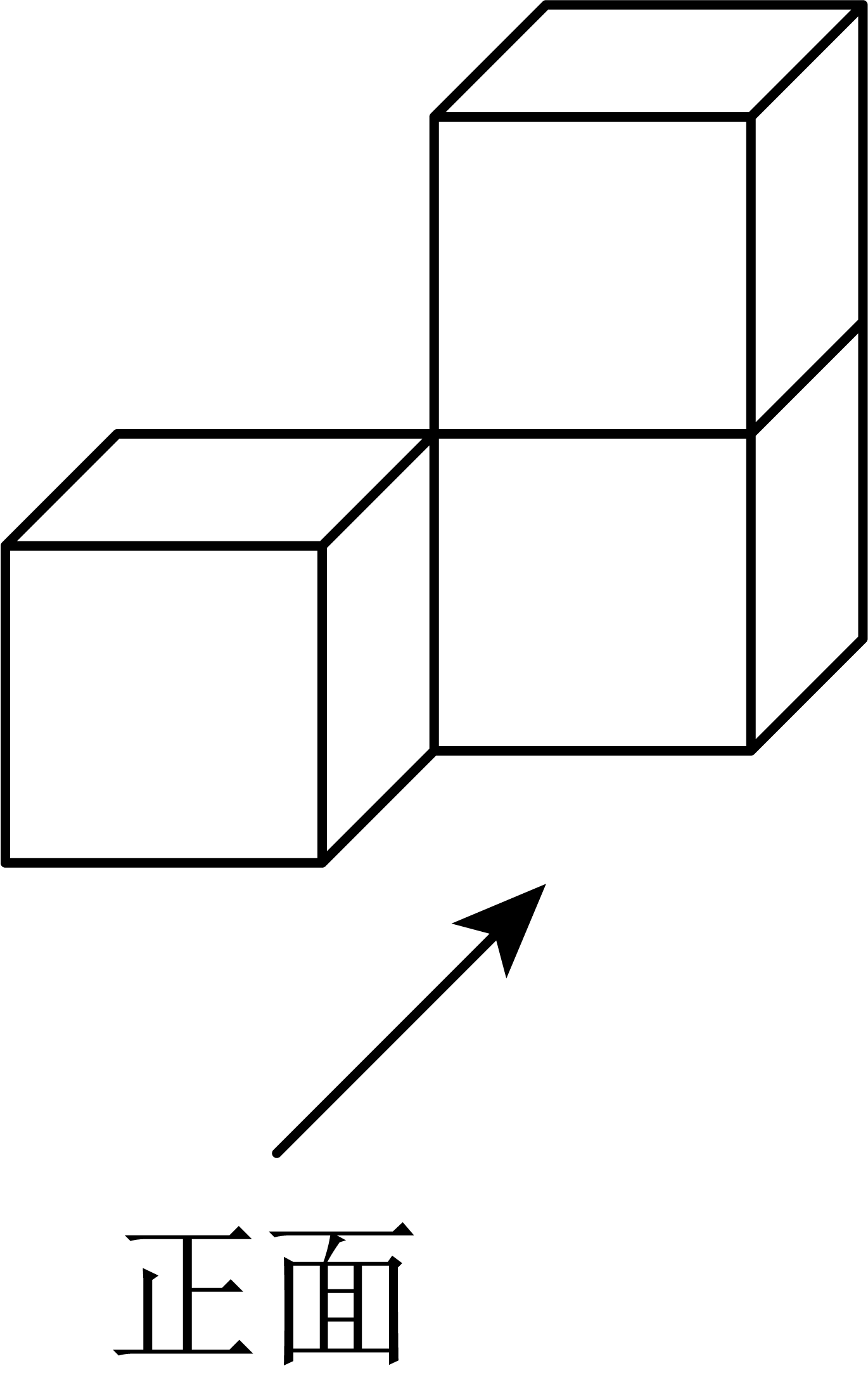A、 B、 C、 D、

查看试题解析
6. 已知反比例函数 $y = \frac{2}{x}$ ，下列结论不正确的是（　　）

A、图象必经过点（1，2） B、在每个象限内，y随x的增大而减小 C、图象在第二、四象限内 D、图象与坐标轴没有交点

查看试题解析
7. 已知a，b是一元二次方程x²+2x﹣1＝0的两根，则 $\frac{2 a}{a^{2} - b^{2}} - \frac{1}{a - b}$ 的值是（　　）

A、 $\frac{1}{2}$ B、2 C、 $- \frac{1}{2}$ D、﹣2

查看试题解析
8. 班长邀请A，B，C，D四位同学参加圆桌会议．如图，班长坐在⑤号座位，四位同学随机坐在①②③④四个座位，则A，B两位同学座位相邻的概率是（　　）

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{1}{4}$ D、 $\frac{2}{3}$

查看试题解析
9. 木匠师傅用长 $A B = 3$ ，宽 $B C = 2$ 的矩形木板做一个尽可能大的圆形桌面，有如下两种方案：
方案一：直接锯一个半径最大的圆；
方案二：沿对角线 $A C$ 将矩形锯成两个三角形，适当平移三角形并锯一个最大的圆．则方案二比方案一的半径大（）

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{1}{4}$ D、 $\frac{1}{5}$

查看试题解析
10. 已知点A（x₁ ， y₁）在抛物线y₁＝nx²﹣2nx+n上，点B（x₂ ， y₂）在直线y₂＝﹣nx+n，当n＞0时，下列判断正确的是（　　）

A、当x₁＝x₂＜1时，y₁＜y₂ B、当x₁＝x₂＞1时，y₁＜y₂ C、当y₁＝y₂＞n时，x₁＞x₂ D、当y₁＝y₂＜n时，x₁＞x₂

查看试题解析

二、填空题（共6小题，每小题3分，共18分）

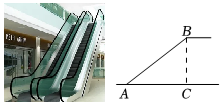
11. 写出一个比4小的正无理数．

查看试题解析
12. 世界文化遗产长城总长约21000千米，数21000用科学记数法表示为．

查看试题解析
13. 如图是某商场营业大厅自动扶梯的示意图，自动扶梯AB的倾斜角为37°，大厅两层之间的距离BC为6m，则自动扶梯AB的长约为 m（参考数据：sin37°≈0.6，cos37°≈0.8，tan37°≈0.75）

查看试题解析
14. 在一次体育课上进行跳绳测试，小明的跳绳平均成绩为每分钟100个，小强的跳绳平均成绩为每分钟150个（单位：个），小明先跳150个，然后小强再跳，如图是小明、小强跳绳的个数关于小强的跳绳时间t的函数图象，则两图象交点P的纵坐标是．

查看试题解析
15. 抛物线y＝ax²+bx+c（a，b，c是常数）经过（1，1），（m，0），（m+2，0），三点，给出下列四个结论：
①a＜0；
②若 $x ＞ \frac{3}{2}$ 时，y随x增加而减少，则 $m = \frac{3}{2}$ ；
③若（m+1，t）在抛物线上，则t＞1；
④b²﹣4ac＝4a²；
其中正确的结论是．（填写序号）

查看试题解析
16. 如图，在等腰 $R t △ A B C$ 中， $A B = B C = 1$ ，点 $E$ ， $F$ 分别是 $A B$ ，连接 $E F$ ，将 $△ A B C$ 沿 $E F$ 翻折，若 $A D = 2 C D$ ，则 $B E$ 的长为．

查看试题解析

三、解答题（共8小题，共72分。解答应写出文字说明、演算步骤或推理过程）

17. 解不等式组 ${\begin{array}{l} 2 x + 1 < - 1 ① \\ 3 x + 5 ⩾ x ② \end{array}$ ，请按下列步骤完成解答：

(1)、解不等式①，得；

(2)、解不等式②，得；

(3)、把不等式①和②的解集在数轴上表示出来；

(4)、原不等式组的解集为．

查看试题解析
18. 如图，点D ， E ， F分别是 $△ A B C$ 的边 $B C$ ， $A C$ ， $A B$ 上的点， $D F ∥ C A$ ， $∠ A = ∠ E D F$ ，

(1)、求证：四边形 $A F D E$ 为平行四边形；

(2)、若 $\frac{B D}{D C} = \frac{3}{5}$ ，直接写出 $\frac{S_{△ B D F}}{S_{△ C D E}}$ 的值为．

查看试题解析

19. 某校开学初对七年级学生进行一次安全知识问答测试，设成绩为

x

分（

x

为整数），将成绩评定为优秀、良好、合格、不合格四个等级（优秀、良好、合格、不合格分别用A、B、C、D表示），A等级：

90 \leq x \leq 100

， B等级：

80 \leq x < 90

， C等级：

60 \leq x < 80

， D等级：

0 \leq x < 60

．该校随机抽取了一部分学生的成绩进行调查，并绘制成如图不完整的统计图表．

等级	频数（人数）
A $(90 \leq x \leq 100)$	$a$
B $(80 \leq x < 90)$	16
C $(60 \leq x < 80)$	$c$
D $(0 \leq x < 60)$	4

请你根据统计图表提供的信息解答下列问题：

(1)、上表中的

a =

，

c =

，

m =

；

(2)、这组数据的中位数所在的等级是；

(3)、该校决定对分数低于80分的学生进行安全再教育，已知该校七年级共有1000名学生，求该校七年级需要进行安全再教育的学生有多少人？

查看试题解析

20. 如图，过矩形 $A B C D$ 顶点A ， B的圆O与 $C D$ 相切于点G ， $B C$ 分别相交于点F ， E ，连接 $A E$ ．

(1)、求证： $E G$ 平分 $∠ C E A$ ；

(2)、若 $A B = 3$ ， $B E = 4$ ，求 $G E$ 的长．

查看试题解析
21. 如图是由小正方形组成的网格，每个小正方形的顶点叫做格点，△ABC中，A是格线上的点，仅用无刻度的直尺在给定网格中完成画图．

(1)、在图（1）中，取AB的中点M；将AC沿着AB方向平移至BD；

(2)、在图（2）中，将线段CB绕C逆时针旋转90°至CE（点E为点B的对应点）；过点E作EF⊥AB于F．

查看试题解析
22. 公路上正在行驶的甲车发现前方 $20 m$ 处沿同一方向行驶的乙车后，开始减速，减速后甲车行驶的路程 $s ($ 单位： $m)$ 、速度 $v ($ 单位： $m / s)$ 与时间 $t ($ 单位： $s)$ 的关系分别可以用二次函数和一次函数表示，其图象如图所示．

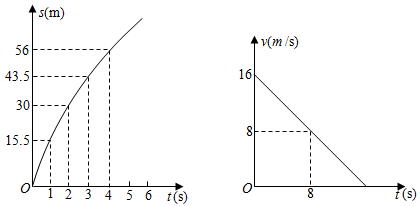(1)、直接写出 $s$ 关于 $t$ 的函数关系式和 $v$ 关于 $t$ 的函数关系式 $($ 不要求写出 $t$ 的取值范围 $)$

(2)、当甲车减速至 $9 m / s$ 时，它行驶的路程是多少？

(3)、若乙车以 $10 m / s$ 的速度匀速行驶，两车何时相距最近，最近距离是多少？

查看试题解析
23. 如图

(1)、问题提出如图（1），在正方形ABCD中，E为AD中点，BF⊥CE，求 $\frac{D F}{C F}$ 的值；

(2)、问题探究如图（2），在等腰Rt△ABC中，点E为AB的中点，BF⊥CE，求 $\frac{F C}{B G}$ 的值．

查看试题解析
24. 如图，在平面直角坐标系中，O为坐标原点，D（0，﹣3），抛物线y＝﹣2x²+6x+8与y轴交于C点，交x轴于A、B两点（A在B的左边），E为抛物线第一象限上一动点．

(1)、直接写出A，B两点坐标；

(2)、连接BD，过E作EF⊥x轴交BD于F，当DF＝CE时，求点E的横坐标；

(3)、连接ED，平移至MN，使M，E对应，使M，N分别与D，E对应，且M，N均落在抛物线上，连接EM，判断并证明直线EM是否经过一个定点．

查看试题解析