广东省深圳市34校2024年中考二模联考数学试题
试卷更新日期:2024-04-26 类型:中考模拟
一、选择题(本大题共10小题,每小题3分,共30分,每小题有四个选项,其中只有一个是正确的)
-
1. 某运动项目比赛规定:胜一场记作“”分,平局记作“0分”.如果某队在一场比赛中得分记作“”分,则该队在这场比赛中( )A、与对手打成平局 B、输给对手 C、赢得对手 D、无法确定2. 窗花是我国古代园林建筑中窗的一种装饰和美化的形式,下列窗花图案中,既是轴对称图形,又是中心对称图形的是( )A、
 B、
B、 C、
C、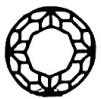 D、
D、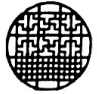 3. 中国海关总署于2024年1月12日发布消息称:2023年我国汽车出口量为522万辆,同比增加57.4%.数据“522万”用科学记数法表示应为( )A、 B、 C、 D、4. 下图是深圳市2024年4月7~11日的天气情况,这5天中最低气温(单位:℃)的中位数与众数分别是( )
3. 中国海关总署于2024年1月12日发布消息称:2023年我国汽车出口量为522万辆,同比增加57.4%.数据“522万”用科学记数法表示应为( )A、 B、 C、 D、4. 下图是深圳市2024年4月7~11日的天气情况,这5天中最低气温(单位:℃)的中位数与众数分别是( )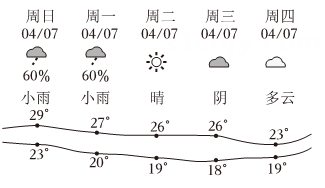 A、19,19 B、19,18 C、18,19 D、20,195. 如图是某款婴儿手推车的平面示意图,若 , 则的度数为( )
A、19,19 B、19,18 C、18,19 D、20,195. 如图是某款婴儿手推车的平面示意图,若 , 则的度数为( ) A、75° B、80° C、85° D、90°6. 下列计算正确的是( )A、 B、 C、 D、7. 如图是一款桌面可调整的学习桌,桌面宽度AB为60cm,桌面平放时高度DE为70cm,若书写时桌面适宜倾斜角的度数为 , 则桌沿(点A)处到地面的高度h为( )
A、75° B、80° C、85° D、90°6. 下列计算正确的是( )A、 B、 C、 D、7. 如图是一款桌面可调整的学习桌,桌面宽度AB为60cm,桌面平放时高度DE为70cm,若书写时桌面适宜倾斜角的度数为 , 则桌沿(点A)处到地面的高度h为( )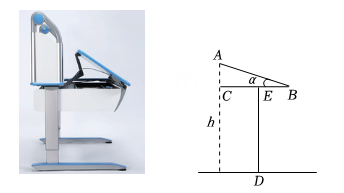
A、 B、 C、 D、8. 在同一直角坐标系中,一次函数的图象如图所示,则下列结论错误的是( )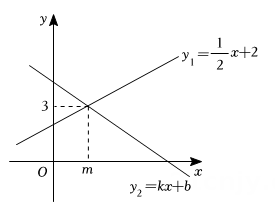 A、随x的增大而减小 B、 C、当时, D、方程组的解为9. 下图是明代数学家程大位所著的《算法统宗》中的一个问题,其大意为:有一群人分银子,如果每人分七两,则剩余四两:如果每人分九两,则还差八两.设共有银子x两,共有y人,则所列方程(组)错误的是( )
A、随x的增大而减小 B、 C、当时, D、方程组的解为9. 下图是明代数学家程大位所著的《算法统宗》中的一个问题,其大意为:有一群人分银子,如果每人分七两,则剩余四两:如果每人分九两,则还差八两.设共有银子x两,共有y人,则所列方程(组)错误的是( )隔壁听得客分银,
不知人数不知银,
七两分之多四两,
九两分之少半斤。
《算法统宗》
注:明代时1斤=16两,故有“半斤八两”这个成语
A、 B、 C、 D、10. 如图(a),A , B是⊙O上两定点, , 圆上一动点P从点B出发,沿逆时针方向匀速运动到点A , 运动时间是 , 线段AP的长度是y(cm).图(b)是y随x变化的关系图象,其中图象与x轴交点的横坐标记为m , 则m的值是( )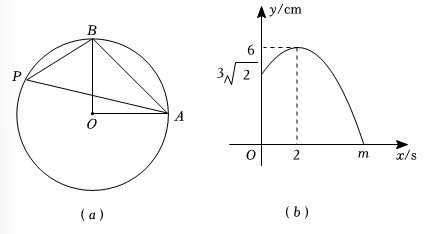 A、8 B、6 C、 D、
A、8 B、6 C、 D、二、填空题(本大题共5小题,每小题3分,共15分)
-
11. = .12. 若关于x的一元二次方程有一个根为0,则 .13. 老师为帮助学生正确理解物理变化与化学变化,将4种生活现象制成如图所示的4张无差别的卡片A , B , C , D . 将卡片背面朝上,小明同学从中随机抽取2张卡片,则所抽取的2张卡片刚好都是物理变化的概率是 .
A
冰化成水
B
酒精燃烧
C
牛奶变质
D
衣服晾干
14. 如图,正比例函数的图象与反比例函数的图象交于A , B两点,过点A的直线分别与x轴、y轴交于C , D两点.当 , 时,则 .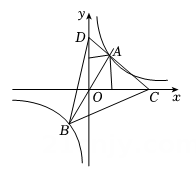 15. 如图,在矩形ABCD中,E是AB的中点,作交BC于点F , 对角线AC分别交DE , DF于点G , H , 当DH⊥AC时,则的值为 .
15. 如图,在矩形ABCD中,E是AB的中点,作交BC于点F , 对角线AC分别交DE , DF于点G , H , 当DH⊥AC时,则的值为 .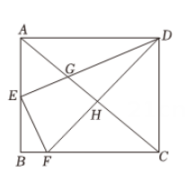
三、解答题(本题共7小题,共55分)
-
16.(1)、计算:;(2)、化简:17. 在直角坐标系中,将进行平移变换,变换前后点的坐标的情况如下表:
变换前
变换后
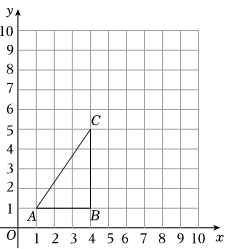 (1)、平移后点的坐标是 , 并在直角坐标系中画出;(2)、若是内一点,通过上述平移变换后,点P的对应点的坐标可表示为;(3)、连接 , , 则四边形的形状是 , 其面积为 .18. 某校学生的上学方式分为“A步行、B骑车、C乘公共交通工具、D乘私家车、E其它”,该校数学兴趣小组成员在全校随机抽取了若干名学生进行抽样调查,并整理样本数据,得到如下两幅不完整的统计图:
(1)、平移后点的坐标是 , 并在直角坐标系中画出;(2)、若是内一点,通过上述平移变换后,点P的对应点的坐标可表示为;(3)、连接 , , 则四边形的形状是 , 其面积为 .18. 某校学生的上学方式分为“A步行、B骑车、C乘公共交通工具、D乘私家车、E其它”,该校数学兴趣小组成员在全校随机抽取了若干名学生进行抽样调查,并整理样本数据,得到如下两幅不完整的统计图: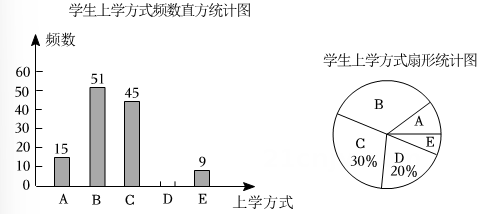 (1)、本次抽样调查的人数为 人,并补全条形统计图;(2)、扇形统计图中“A步行”上学方式所对的圆心角是度;(3)、若该校共2000名学生,请估计该校“B骑车”上学的人数约是人;(4)、该校数学兴趣小组成员结合调查获取的信息,向学校提出了一些建议.
(1)、本次抽样调查的人数为 人,并补全条形统计图;(2)、扇形统计图中“A步行”上学方式所对的圆心角是度;(3)、若该校共2000名学生,请估计该校“B骑车”上学的人数约是人;(4)、该校数学兴趣小组成员结合调查获取的信息,向学校提出了一些建议.如:骑车上学的学生超过全校学生总人数的30%,建议学校合理安排自行车停车场地.
请你结合上述统计的全过程,再提出一条合理化建议.
19. 为培养学生的阅读能力,深圳市某校八年级购进《朝花夕拾》和《西游记》两种书籍,分别花费了14000元和7000元,已知《朝花夕拾》的订购单价是《西游记》的订购单价的1.4倍。并且订购的《朝花夕拾》的数量比《西游记》的数量多300本.(1)、求该校八年级订购的两种书籍的单价分别是多少元;(2)、该校八年级计划再订购这两种书籍共100本作为备用,其中《朝花夕拾》订购数量不低于30本,且两种书总费用不超过1200元,请求出再订购这两种书籍的最低总费用的方案及最低费用为多少元?20. 如图,以的边AB为直径作分别交AC , BC于点D , E , 过点E作 , 垂足为F , EF与AB的延长线交于点G .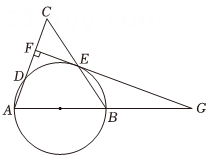 (1)、以下条件:
(1)、以下条件:①E是劣弧BD的中点:
②;
③ .
请从中选择一个能证明EF是的切线的条件,并写出证明过程:(2)、若EF是是的切线,且 , 求BG的长.21. 【项目化学习】项目主题:从函数角度重新认识“阻力对物体运动的影响”.
项目内容:数学兴趣小组对一个静止的小球从斜坡滚下后,在水平木板上运动的速度、距离与时间的关系进行了深入探究,兴趣小组先设计方案,再进行测量,然后根据所测量的数据进行分析,并进一步应用。
实验过程:如图(a)所示,一个黑球从斜坡顶端由静止滚下沿水平木板直线运动,从黑球运动到点A处开始,用频闪照相机、测速仪测量并记录黑球在木板上的运动时间x(单位:s)、运动速度v(单位:cm/s)、滑行距离y(单位:cm)的数据.
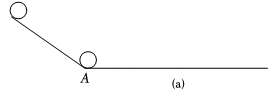
任务一:数据收集
记录的数据如下:
运动时间x/s
0
2
4
6
8
10
…
运动速度v/(cm/s)
10
9
8
7
6
5
…
滑行距离y/cm
0
19
36
51
64
75
…
根据表格中的数值分别在图(b)、图(c)中作出v与x的函数图象、y与x的函数图象:
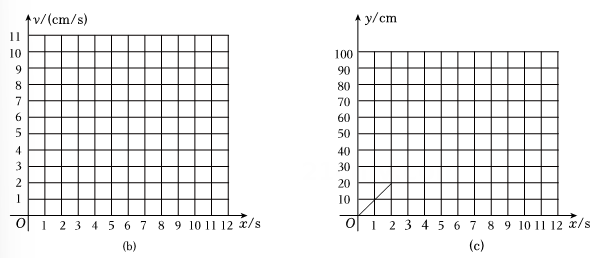 (1)、请在图(b)中画出v与x的函数图象:(2)、【任务二:观察分析】数学兴趣小组通过观察所作的函数图象,并结合已学习过的函数知识,发现图(b)中v与x的函数关系为一次函数关系,图(c)中y与x的函数关系为二次函数关系.请你结合表格数据,分别求出v与x的函数关系式和y与x的函数关系式:(不要求写出自变量的取值范围)(3)、【任务三:问题解决】当黑球在水平木板停下来时,求此时黑球的滑行距离:(4)、若黑球到达木板点A处的同时,在点A的前方处有一辆电动小车,以2cm/s的速度匀速向右直线运动,若黑球不能撞上小车,则n的取值范围应为 .22. 综合与探究.
(1)、请在图(b)中画出v与x的函数图象:(2)、【任务二:观察分析】数学兴趣小组通过观察所作的函数图象,并结合已学习过的函数知识,发现图(b)中v与x的函数关系为一次函数关系,图(c)中y与x的函数关系为二次函数关系.请你结合表格数据,分别求出v与x的函数关系式和y与x的函数关系式:(不要求写出自变量的取值范围)(3)、【任务三:问题解决】当黑球在水平木板停下来时,求此时黑球的滑行距离:(4)、若黑球到达木板点A处的同时,在点A的前方处有一辆电动小车,以2cm/s的速度匀速向右直线运动,若黑球不能撞上小车,则n的取值范围应为 .22. 综合与探究.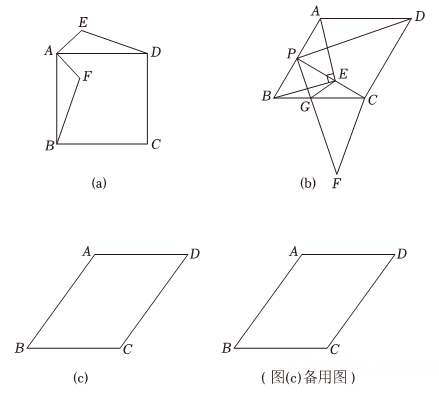 (1)、【特例感知】
(1)、【特例感知】如图(a),E是正方形ABCD外一点,将线段AE绕点A顺时针旋转得到AF , 连接DE , BF . 求证:;
(2)、【类比迁移】如图(b),在菱形ABCD中, , P是AB的中点,将线段PA , PD分别绕点P顺时针旋转得到PE , PF , PF交BC于点G , 连接CE , CF , 求四边形CEGF的面积:
(3)、【拓展提升】如图(c),在平行四边形ABCD中,为锐角且满足 . P是射线BA上一动点,点C , D同时绕点P顺时针旋转得到点 , , 当为直角三角形时,直接写出BP的长.