陕西省西安市莲湖区2023-2024学年七年级下学期数学期中考试试卷
试卷更新日期:2024-04-26 类型:期中考试
一、选择题(本大题共8个小题,每小题3分,共24分.在每个小题给出的四个选项中,只有一项符合题目要求)
-
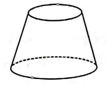
1. 计算-3-1的结果是( )A、2 B、-2 C、4 D、-42. 下面的立体图形是由哪个平面图形绕轴旋转一周得到的( )
 A、
A、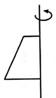 B、
B、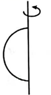 C、
C、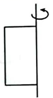 D、
D、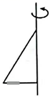 3. 2023年9月13日,记者从省国资委获悉:上半年,省属企业立足加快建设现代化产业体系,充分发挥科技创新骨干支撑和带头示范作用,投入研发经费96.3亿元,同比增长27.3%;新产品产值463.4亿元,同比增长32%,保持高速增长态势.其中数据463.4亿用科学记数法表示为( )A、 B、 C、 D、4. 下列图形中,不是正方体表面展开图的是( )A、
3. 2023年9月13日,记者从省国资委获悉:上半年,省属企业立足加快建设现代化产业体系,充分发挥科技创新骨干支撑和带头示范作用,投入研发经费96.3亿元,同比增长27.3%;新产品产值463.4亿元,同比增长32%,保持高速增长态势.其中数据463.4亿用科学记数法表示为( )A、 B、 C、 D、4. 下列图形中,不是正方体表面展开图的是( )A、 B、
B、 C、
C、 D、
D、 5. 检测两个足球质量(单位:克),超过标准质量记为正,低于标准质量记为负,若②号足球的质量更接近标准质量,则②号足球的质量可以记为( )
5. 检测两个足球质量(单位:克),超过标准质量记为正,低于标准质量记为负,若②号足球的质量更接近标准质量,则②号足球的质量可以记为( ) A、+0.5 B、+2 C、-0.7 D、-16. 计算的结果是( )A、0 B、4 C、2 D、-27. 下列各组数中,数值相等的是( )A、和 B、和 C、和 D、和8. 根据如图所示的程序计算下列代数式的值,若输入的x的值为-2,则输出y的值是( )
A、+0.5 B、+2 C、-0.7 D、-16. 计算的结果是( )A、0 B、4 C、2 D、-27. 下列各组数中,数值相等的是( )A、和 B、和 C、和 D、和8. 根据如图所示的程序计算下列代数式的值,若输入的x的值为-2,则输出y的值是( ) A、4 B、 C、 D、0
A、4 B、 C、 D、0二、填空题(本大题共5个小题,每小题3分,共15分)
-
9. -5的相反数是 .10. 用一个平面截下列几何体:①正方体;②球;③圆柱;④五棱柱,截面可能是圆的是 . (填写序号即可)11. 如果 , 那么的值为 .12. 计算的结果是 .13. 1883年,康托尔用以下的方法构造的这个分形,称做康托尔集.如图,取一条长度为1的线段,将它三等分,去掉中间一段,留剩下两段,这称为第一阶段;然后将剩下的两段再三等分,各去掉中间一段,剩下更短的四段,这称为第二阶段;…,将这样的操作无限地重复下去,余下的无穷点就称做康托尔集.那么经过第四阶段后,留下的线段的长度之和为 .

三、解答题(本大题共13个小题,共81分.解答应写出文字说明、证明过程或演算步骤)
-
14. 把下列数填在相应的集合内.
, 0,-3.5,1.2,6.
(1)、负分数集合:{ ……}.(2)、非负数集合:{ ……}.15. 计算: .16.(1)、绝对值是1的数有几个?各是什么?(2)、绝对值是0的数有几个?各是什么?(3)、绝对值是-2022的数是否存在?若存在,请写出来.17. 如图,这是一个五直棱柱,若它的底面边长都是2cm,侧棱长都是5cm,回答下列问题: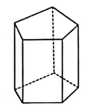 (1)、它有,个侧面,个底面.(2)、它的所有侧面的面积之和是多少?18. 如图,某数学活动小组编制了一道有理数的混合运算题,即输入一个有理数,按照自左向右的顺序运算,可得计算结果,其中“●”表示最大的负整数,若输入的数为-4,求计算结果.
(1)、它有,个侧面,个底面.(2)、它的所有侧面的面积之和是多少?18. 如图,某数学活动小组编制了一道有理数的混合运算题,即输入一个有理数,按照自左向右的顺序运算,可得计算结果,其中“●”表示最大的负整数,若输入的数为-4,求计算结果. 19. 小明在计算时,采用的方法如下:
19. 小明在计算时,采用的方法如下:原式 .
请你判断小明的计算过程是否正确,若不正确,请写出正确的计算过程.
20. 如图,这是由6个大小相同的小立方体块搭建而成的几何体.请按要求在方格内分别画出从这个几何体的三个不同方向看到的形状图. 21. 某学校七年级为庆祝国庆节,同时培养学生团结协作和凝心聚力的能力,举行主题为“一根绳一条心”的拔河比赛活动.在七(1)班和七(2)班两个班级的比赛过程中,标志红绳开始先向七(2)班方向移动了0.3米,接着向七(1)班方向移动了0.4米,相持一会后,又向七(2)班方向移动了0.5米,随后又向七(1)班方向移动了0.9米,僵持一段时间后,标志红绳又向七(1)班方向移动了1.1米.若规定标志红绳从开始中心位置向某班级方向移动1.5米后该班级即可获胜,根据上述数据变化能否判断哪个班级赢了,请通过计算说明你的判断.22. 已知a是负数,且其绝对值是 , b的倒数是 , m和n互为相反数,求的值.23. 如图,老师在黑板上写了一道计算题,计算: .
21. 某学校七年级为庆祝国庆节,同时培养学生团结协作和凝心聚力的能力,举行主题为“一根绳一条心”的拔河比赛活动.在七(1)班和七(2)班两个班级的比赛过程中,标志红绳开始先向七(2)班方向移动了0.3米,接着向七(1)班方向移动了0.4米,相持一会后,又向七(2)班方向移动了0.5米,随后又向七(1)班方向移动了0.9米,僵持一段时间后,标志红绳又向七(1)班方向移动了1.1米.若规定标志红绳从开始中心位置向某班级方向移动1.5米后该班级即可获胜,根据上述数据变化能否判断哪个班级赢了,请通过计算说明你的判断.22. 已知a是负数,且其绝对值是 , b的倒数是 , m和n互为相反数,求的值.23. 如图,老师在黑板上写了一道计算题,计算: . (1)、该计算题的正确结果是 .(2)、老师在同学们计算完后,对该题进行了变式,计算: . 请完成变式的计算.24. 约定:上方相邻两数之和等于这两数下方箭头共同指向的数.
(1)、该计算题的正确结果是 .(2)、老师在同学们计算完后,对该题进行了变式,计算: . 请完成变式的计算.24. 约定:上方相邻两数之和等于这两数下方箭头共同指向的数. (1)、如图2,用含有x的式子表示: , .(2)、如图2,若 , 求y的值.25. 在数学综合实践活动课上,小明将一个无盖鞋盒拆开并展开,如图,若展开后的长与宽分别记为a cm,b cm,在纸盒四个角上的空白处均为边长为x cm的正方形.
(1)、如图2,用含有x的式子表示: , .(2)、如图2,若 , 求y的值.25. 在数学综合实践活动课上,小明将一个无盖鞋盒拆开并展开,如图,若展开后的长与宽分别记为a cm,b cm,在纸盒四个角上的空白处均为边长为x cm的正方形. (1)、用a , b , x表示无盖鞋盒拆开后展开的面积(即阴影的面积).(2)、用a , b , x表示无盖鞋盒的体积.(表示成长×宽×高即可,不用展开)(3)、当 , , 时,求该无盖鞋盒的体积.26. 小辉在电脑屏幕上,设计了一条数轴,在数轴上标有两个点A , B , 点A表示数-32,且A , B两点间的距离为60个单位长度,点P从点A出发,第一次沿数轴向左运动2个单位长度,第二次沿数轴向右运动4个单位长度,第三次沿数轴向左运动6个单位长度,第四次沿数轴向右运动8个单位长度,…,且按此规律进行运动.
(1)、用a , b , x表示无盖鞋盒拆开后展开的面积(即阴影的面积).(2)、用a , b , x表示无盖鞋盒的体积.(表示成长×宽×高即可,不用展开)(3)、当 , , 时,求该无盖鞋盒的体积.26. 小辉在电脑屏幕上,设计了一条数轴,在数轴上标有两个点A , B , 点A表示数-32,且A , B两点间的距离为60个单位长度,点P从点A出发,第一次沿数轴向左运动2个单位长度,第二次沿数轴向右运动4个单位长度,第三次沿数轴向左运动6个单位长度,第四次沿数轴向右运动8个单位长度,…,且按此规律进行运动. (1)、求点B表示的数.(2)、设点P运动第七次后所表示的数为m , 第八次运动后所表示的数为n , 求m与n的积.(3)、经过100次运动后,求点P所在的位置与点B之间的距离.
(1)、求点B表示的数.(2)、设点P运动第七次后所表示的数为m , 第八次运动后所表示的数为n , 求m与n的积.(3)、经过100次运动后,求点P所在的位置与点B之间的距离.