广西壮族自治区柳州市2024年初中学业水平考试模拟试卷数学模拟试题
试卷更新日期:2024-04-26 类型:中考模拟
一、选择题(每题3分,共36分)
-
1. -2024的相反数是( )A、 B、2024 C、 D、2. 下列图形中具有稳定性的图形是( )A、
 B、
B、 C、
C、 D、
D、 3. 如图是一个小正方体的展开图,把展开图折叠成小正方体后,有“点”字一面的相对面上的字是( )
3. 如图是一个小正方体的展开图,把展开图折叠成小正方体后,有“点”字一面的相对面上的字是( ) A、青 B、春 C、梦 D、想4. 描述柳州市某一周内每天最高气温的变化趋势,最合适的统计图是( )A、条形统计图 B、折线统计图 C、扇形统计图 D、频数分布直方图.5. 如图, , , 则的度数是( )
A、青 B、春 C、梦 D、想4. 描述柳州市某一周内每天最高气温的变化趋势,最合适的统计图是( )A、条形统计图 B、折线统计图 C、扇形统计图 D、频数分布直方图.5. 如图, , , 则的度数是( ) A、100° B、110° C、120° D、140°6. 把不等式的解集在数轴上表示出来,则正确的是( )A、
A、100° B、110° C、120° D、140°6. 把不等式的解集在数轴上表示出来,则正确的是( )A、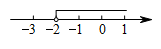 B、
B、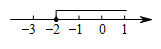 C、
C、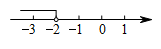 D、
D、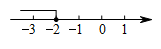 7. 下列汽车标志中,是中心对称图形的是( )A、
7. 下列汽车标志中,是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 8. 如图,直线a,b被直线c所截,若 , , 则的度数是( )
8. 如图,直线a,b被直线c所截,若 , , 则的度数是( ) A、70° B、100° C、110° D、120°9. 把多项式分解因式得( )A、 B、 C、 D、10. 我国古代数学名著《张邱建算经》中记载:“今有清酒一斗直粟十斗,醑酒一斗直粟三斗.今持粟三斛,得酒五斗,问清、醕酒各几何?意思是:现在一斗清酒价值10斗谷子,一斗醑酒价值3斗谷子,现在拿30斗谷子,共换了5斗酒,问清、醑酒各几斗?如果设清酒斗,醑酒斗,那么可列方程组为( )A、 B、 C、 D、11. 若二次函数的部分图象如图所示,则关于的方程的解为( )
A、70° B、100° C、110° D、120°9. 把多项式分解因式得( )A、 B、 C、 D、10. 我国古代数学名著《张邱建算经》中记载:“今有清酒一斗直粟十斗,醑酒一斗直粟三斗.今持粟三斛,得酒五斗,问清、醕酒各几何?意思是:现在一斗清酒价值10斗谷子,一斗醑酒价值3斗谷子,现在拿30斗谷子,共换了5斗酒,问清、醑酒各几斗?如果设清酒斗,醑酒斗,那么可列方程组为( )A、 B、 C、 D、11. 若二次函数的部分图象如图所示,则关于的方程的解为( ) A、 , B、 , C、 , D、 ,12. 如图,在中, , , 是的中点,连接 , 过点作交于点 , 若的面积为6,则的面积为( )
A、 , B、 , C、 , D、 ,12. 如图,在中, , , 是的中点,连接 , 过点作交于点 , 若的面积为6,则的面积为( ) A、144 B、150 C、288 D、72
A、144 B、150 C、288 D、72二、填空题(每小题2分,共12分.)
-
13. 如果某天的温度上升了5℃记作 , 那么温度下降5℃记作.14. 某校举办“清廉校园建设”演讲比赛,评分办法采用5位评委现场打分,5位评委给某位选手打分分别是:9.8,9.7,9.6,9.5,9.5.则这组数据的中位数为.15. 如图,点 , , 在上, , 则的度数是°.
 16. 如图,有一斜坡 , 此斜坡的坡面长 , 斜坡的坡角是 , 若 , 则坡顶离地面的高度为.
16. 如图,有一斜坡 , 此斜坡的坡面长 , 斜坡的坡角是 , 若 , 则坡顶离地面的高度为. 17. 如图,在中, , , 分别以点和点为圆心,大于的长为半径作弧,两弧相交于 , 两点,作直线 , 分别交 , 于点 , .则的长为.
17. 如图,在中, , , 分别以点和点为圆心,大于的长为半径作弧,两弧相交于 , 两点,作直线 , 分别交 , 于点 , .则的长为.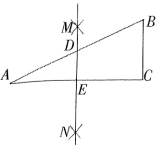 18. 如图,将图1中的菱形纸片沿对角线剪成4个直角三角形,拼成如图2的四边形(相邻纸片之间不重叠,无謎隙).若四边形的面积为13,中间空白处的四边形的面积为1,直角三角形的两条直角边分别为 , , 则.
18. 如图,将图1中的菱形纸片沿对角线剪成4个直角三角形,拼成如图2的四边形(相邻纸片之间不重叠,无謎隙).若四边形的面积为13,中间空白处的四边形的面积为1,直角三角形的两条直角边分别为 , , 则.
图1 图2
三、解答题(本大题共8小题,共72分.解答应写出文字说明、证明过程或演算步骤.)
-
19. 计算:.20. 解方程组:.21. 如图,点 , , , 在同一条直线上, , , .
 (1)、求证:;(2)、求证:.22. 某市开展党史知识竞赛活动,某单位决定从报名的 , , 三名优秀党员中通过抽签的方式确定两名优秀党员参加.将三名优秀党员的名字分别写在3张完全相同不透明卡片的正面,把这3张卡片背面朝上,洗匀后放在桌上,先从中随机抽取1张卡片,记下名字后,再从剩下的2张卡片中随机抽取1张,记下名字.(1)、第一次从3张卡片中随机抽取1张卡片,优秀党员被选中的概率是;(2)、请用列表或画树状图的方法,求出 , 两名优秀党员被选中的概率.23. 如图,在平面直角坐标系中,二次函数的图像与轴交于 , 两点,点的坐标为 , 与轴交于点 , 点为抛物线的顶点
(1)、求证:;(2)、求证:.22. 某市开展党史知识竞赛活动,某单位决定从报名的 , , 三名优秀党员中通过抽签的方式确定两名优秀党员参加.将三名优秀党员的名字分别写在3张完全相同不透明卡片的正面,把这3张卡片背面朝上,洗匀后放在桌上,先从中随机抽取1张卡片,记下名字后,再从剩下的2张卡片中随机抽取1张,记下名字.(1)、第一次从3张卡片中随机抽取1张卡片,优秀党员被选中的概率是;(2)、请用列表或画树状图的方法,求出 , 两名优秀党员被选中的概率.23. 如图,在平面直角坐标系中,二次函数的图像与轴交于 , 两点,点的坐标为 , 与轴交于点 , 点为抛物线的顶点 (1)、求这个二次函数的解析式;(2)、求的面积24. 如图,内接于 , 是的直径,与相切于点 , 交的延长线于点 , 为的中点,连接、.
(1)、求这个二次函数的解析式;(2)、求的面积24. 如图,内接于 , 是的直径,与相切于点 , 交的延长线于点 , 为的中点,连接、. (1)、求证:是的切线;(2)、已知 , , 求.25. 某生物小组探究“酒精对人体的影响”,资料显示,一般饮用低度白酒100毫升后,血液中酒精含量(毫克/百毫升)与时间(时)的关系可近似的用如图所示的图象表示.国家规定,人体血液中的酒精含量大于或等于20(毫克/百毫升)时属于“酒后驾驶”,不能驾车上路.
(1)、求证:是的切线;(2)、已知 , , 求.25. 某生物小组探究“酒精对人体的影响”,资料显示,一般饮用低度白酒100毫升后,血液中酒精含量(毫克/百毫升)与时间(时)的关系可近似的用如图所示的图象表示.国家规定,人体血液中的酒精含量大于或等于20(毫克/百毫升)时属于“酒后驾驶”,不能驾车上路. (1)、求部分双曲线的函数表达式;(2)、参照上述数学模型,假设某人晚上20:00喝完100毫升低度白酒,则此人第二天早上9:00能否驾车出行?请说明理由.26. 综合与实践
(1)、求部分双曲线的函数表达式;(2)、参照上述数学模型,假设某人晚上20:00喝完100毫升低度白酒,则此人第二天早上9:00能否驾车出行?请说明理由.26. 综合与实践小明在刘老师的指导下开展“探究四点共圆的条件”活动,得出结论:对角互补的四边形四个顶点共圆.小明继续利用上述结论进行探究.

图1 图2 图3
【提出问题】
如图1,在线段同侧有两点 , , 连接 , , , , 如果 , 那么 , , , 四点在同一个圆上.
探究展示:
如图2,作经过点 , , 的 , 在劣弧上取一点(不与 , 重合),连接 , ,
则
又∵ ,
∴ ▲ ,
∴点 , , , 四点在同一个圆上(对角互补的四边形四个顶点共圆),
∴点 , 在点 , , 所确定的上
∴点 , , , 四点在同一个圆上.
(1)、【反思归纳】上述探究过程中的横线上填的内容是;(2)、【拓展延伸】如图3,在中, , , 将绕点逆时针旋转得 , 连接交于点 , 连接、.小明发现,在旋转过程中,永远等于45°,不会发生改变.①根据 , 利用四点共圆的思想,试证明;
②在(1)的条件下,当为直角三角形,且时,直接写出的长.