湖北省襄阳市第三十一中学2023-2024学年九年级下学期月考数学试题

试卷更新日期：2024-04-26 类型：月考试卷

进入出卷网下载

一、用心选一选：（本大题共l0个小题，每小题3分，共30分）

1. 下列数各数中，最小的是（）

A、 $- 1$ B、 $- 2$ C、 $2$ D、 $0$

查看试题解析
2. 根据有关部门测算，2022年春节假期7天，全国国内旅游出游251000000人次，数据251000000用科学记数法表示为（）

A、2.51×10⁸ B、2.51×10⁷ C、25.1×10⁷ D、0.251×10⁹

查看试题解析
3. 下列各式中运算正确的是（）

A、 $(- 18) \div (- 9) = - 2$ B、 $(- 2)^{3} = - 8$ C、 $2 x^{3} + 3 x^{3} = 5 x^{6}$ D、 $a^{2} b - a b^{2} = 0$

查看试题解析
4. 不等式 $x - 1 > 0$ 的解在数轴上表示为（　　　）

A、 B、 C、 D、

查看试题解析
5. 下列计算正确的是（）

A、 $2 \sqrt{3} - \sqrt{3} = 2$ B、 $\sqrt{21} \div 3 = \sqrt{7}$ C、 ${(- a)}^{2} \cdot a = a^{3}$ D、 ${(a - 1)}^{2} = a^{2} - 1$

查看试题解析
6. 如图，在 $△ A B C$ 中， $∠ B = 30 °$ ， $B C$ 的垂直平分线交 $A B$ 于点E，垂足为D， $C E$ 平分 $∠ A C B$ ，若 $A E = 1$ ，则 $B E$ 的长为（）

A、 $\sqrt{3}$ B、1 C、 $\sqrt{2}$ D、2

查看试题解析
7. 如图，AC⊥BE ， DE⊥BE ，若△ABC≌△BDE ， AC=5，DE=2，则CE等于（）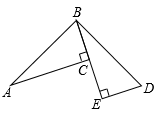

A、2.5 B、3 C、3.5 D、4

查看试题解析
8. 如图，将一副三角板 $(∠ A = 30 °)$ 按如图所示方式摆放，使得 $A B ∥ E F$ ，则 $∠ 1$ 等于（）

A、 $75 °$ B、 $90 °$ C、 $105 °$ D、 $115 °$

查看试题解析
9. 对于反比例函数 $y = - \frac{6}{x}$ ，下列结论：
$①$ 图象分布在第二，四象限； $②$ 当 $x < 0$ 时， $y$ 随 $x$ 的增大而增大； $③$ 从图象上任意一点作两坐标轴的垂线，与坐标轴围成的矩形面积都是 $6$ ； $④$ 若点 $A (x_{1}, y_{1})$ ， $B (x_{2}, y_{2})$ 都在图象上，且 $x_{1} < x_{2}$ ，则 $y_{1} < y_{2}$ ；
其中正确的是（）

A、 $① ② ③$ B、 $② ③ ④$ C、 $① ③ ④$ D、 $① ② ③ ④$

查看试题解析
10. 如图，抛物线 $y = a x^{2} + b x + c （ a \neq 0 ）$ 的顶点坐标为 $(- 1 ， 3)$ ，下列说法错误的是（）

A、 $a < 0$ B、 $4 a c - b^{2} ＜ 0$ C、抛物线向下平移 c个单位后，一定经过 $(- 2 ， 0)$ D、 $\frac{b}{2 a} = - 1$

查看试题解析

二、细心填一填（本大题共5小题，每小题3分，满分15分）

11. 化简： $\frac{x}{x - 1} + \frac{2 x - 1}{1 - x}$ ＝．

查看试题解析
12. 函数y＝ $\frac{\sqrt{x + 1}}{x^{2} + 1}$ 中，自变量x的取值范围是．

查看试题解析
13. 在实数范围内分解因式： $2 x^{2} - 4$ = ．

查看试题解析
14. 汽车刹车后行驶的距离 $s$ (单位：米)关于时间 $t$ (单位：秒)的函数关系式是 $s = 15 t - 6 t^{2}$ ，则汽车从刹车到停止滑行的距离为m．

查看试题解析
15. 在△ABC中，AB=12 $\sqrt{2}$ ， AC=13，cos∠B= $\frac{\sqrt{2}}{2}$ ，则BC边长为．

查看试题解析

三、专心解一解（本大题共9小题，满分75分）

16. 计算： ${(- 2024)}^{0} - 2 t a n 45 ° + | - 2 | + \sqrt{9} - {(- \frac{1}{2})}^{- 2}$ ．

查看试题解析
17. 如图，点C，E，F，B在同一直线上，点A，D在BC异侧，AB∥CD，AE＝DF，∠A＝∠D．

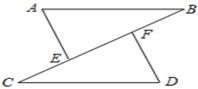(1)、求证：AB＝CD；

(2)、若AB＝CF，∠B＝40°，求∠D的度数．

查看试题解析
18. 已知关于x的方程 $x^{2} - 2 (k - 1) x + k^{2} = 0$ 有两个实数根x₁ ， x₂.

(1)、求k的取值范围；

(2)、若 $x_{1} + x_{2} = 1 - x_{1} x_{2}$ ，求k的值.

查看试题解析
19. 某公司购买了一批A、B型芯片，其中A型芯片的单价比B型芯片的单价少9元，已知该公司用3120元购买A型芯片的条数与用4200元购买B型芯片的条数相等．

(1)、求该公司购买的A、B型芯片的单价各是多少元？

(2)、若两种芯片共购买了200条，且购买的总费用为6280元，求购买了多少条A型芯片？

查看试题解析
20. 如图，已知反比例函数 $y_{1} = \frac{k_{1}}{x}$ 的图象与直线 $y_{2} = k_{2} x + b$ 相交于 $A (- 1, 3)$ ， $B (3, n)$ 两点．

(1)、求反比例函数与一次函数的解析式；

(2)、求△AOB的面积；

(3)、直接写出当 $y_{1} > y_{2}$ 时，对应的x的取值范围．

查看试题解析
21. 位于岘山的革命烈士纪念塔是襄阳市的标志性建筑，是为纪念“襄樊战役”中牺牲的革命烈士及第一、第二次国内革命战争时期为襄阳的解放事业献身的革命烈士的而兴建的，某校数学兴趣小组利用无人机测量纪念塔的高度．无人机在点A处测得纪念塔顶部点B的仰角为45°，纪念塔底部点C的俯角为61°，无人机与纪念塔的水平距离AD为10m，求纪念塔的高度．（结果保留整数．参考数据：sin61°≈0.87，cos61°≈0.48，tan61°≈1.80）

查看试题解析
22. 某商品的进价为每件40元，售价为每件50元，每个月可卖出210件，如果每件商品的售价上涨1元，则每个月少卖10件（每件售价不能高于65元），设每件商品的售价上涨x元（x为正整数），每个月的销售利润为y元，

(1)、若每件商品的售价定价为55元，则每个月可卖出件；

(2)、每件商品的售价定为多少元时，每个月可获得最大利润？最大的月利润是多少元？

(3)、若在销售过程中每一件商品有a（a＞2）元的其他费用，商家发现当售价每件不低于57元时，每月的销售利润随x的增大而减小，请求出a的取值范围．

查看试题解析
23. 如图

(1)、观察猜想：
如图1，在直角 $△ A B C$ 中， $∠ B A C = 90 °$ ， $A B = A C$ ，点D为 $B C$ 边上一动点（与点B不重合），连接 $A D$ ，将 $△ A B D$ 绕点A逆时针旋转 $90 °$ 到 $△ A C E$ ，那么 $C E$ 、 $B D$ 之间的位置关系为，数量关系为；

(2)、数学思考：
如图2，在 $△ A B C$ 中， $∠ C A B = 90 °$ ， $A B = A C$ ， D、E为 $B C$ 上两点，且 $∠ D A E = 45 °$ ，求证： $B D^{2} + C E^{2} = D E^{2}$ ．

(3)、拓展延伸：
如图3，在 $△ A B C$ 中， $∠ C A B = 120 °$ ， $A B = A C$ ， $∠ D A E = 60 °$ ，若以 $B D$ 、 $D E$ 、 $E C$ 为边的三角形是以 $B D$ 为斜边的直角三角形，当 $B D = 2$ 时，求 $D E$ 的长．

查看试题解析
24. 如图所示，在平面直角坐标系中，已知抛物线y=ax²+bx－5与x轴交于A(-1，0)，B(5，0)两点，与y轴交于点C．

(1)、求抛物线的解析式；

(2)、如图2所示，CE∥x轴与抛物线相交于点E，点H是直线CE下方抛物线上的动点，过点H且与y轴平行的直线与BC、CE分别交于点F、G，试探究当点H运动到何处时，四边形CHEF的面积最大，求点H的坐标及最大面积；

(3)、点M是（1）中所求抛物线对称轴上一动点，点N是反比例函数y= $\frac{k}{x}$ 图象上一点，若以点B、C、M、N为顶点的四边形是矩形，请直接写出满足条件的k的值．

查看试题解析