湖北省孝感市高新区2024年中考一模数学试题

试卷更新日期：2024-04-26 类型：中考模拟

进入出卷网下载

一、选择题（共10题，每题3分，共30分。在每题给出的四个选项中，只有一项符合题目要求）

1. $- 5$ 的相反数是（）

A、 $- \frac{1}{5}$ B、 $\frac{1}{5}$ C、5 D、 $- 5$

查看试题解析
2. 如图是某几何体的视图，该几何体是（）

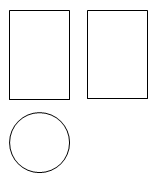A、圆柱 B、球 C、三棱柱 D、长方体

查看试题解析
3. 第十四届全国人民代表大会第二次会议2024年3月5日在北京人民大会堂开幕．李强总理在政府工作报告中回顾过去一年，成绩来之不易、鼓舞人心——国内生产总值超过126万亿元．将126000000000000用科学记数法表示为（）

A、 $126 \times 1 0^{12}$ B、 $12.6 \times 1 0^{13}$ C、 $1.26 \times 1 0^{14}$ D、 $0.126 \times 1 0^{15}$

查看试题解析
4. 下列计算正确的是（）

A、 $a + a = a^{2}$ B、 ${(2 a)}^{3} = 6 a^{3}$ C、 ${(a - 1)}^{2} = a^{2} - 1$ D、 $a^{3} \div a = a^{2}$

查看试题解析
5. 下列说法正确的是（）

A、如果明天降水的概率是 $50 %$ ，那么明天有半天都在降雨 B、若甲、乙两组数据的平均数相同， $S_{甲}^{2} = 1.3, S_{乙}^{2} = 4.6$ ，则乙组数据较稳定 C、了解孝感市学生的“双减”情况应选用全面调查 D、早上的太阳从东方升起是必然事件

查看试题解析
6. 若 $x_{1}$ 和 $x_{2}$ 是一元二次方程 $2 x^{2} + x - 2 = 0$ 的两个实数根，则 $x_{1} + x_{2} + x_{1} x_{2} =$ （）

A、 $- 1$ B、 $- \frac{1}{2}$ C、 $- \frac{3}{2}$ D、 $- 4$

查看试题解析
7. 如图，一束光线 $A B$ 先后经平面镜 $O M, O N$ 反射后，反射光线 $C D$ 与 $A B$ 平行，当 $∠ A B M = 35 °$ 时， $∠ D C B$ 的度数是（）

A、 $55 °$ B、 $70 °$ C、 $60 °$ D、 $35 °$

查看试题解析
8. 如果一个多边形的每个内角都相等，且内角和为 $2340 °$ ，那么这个多边形的一个外角的度数为（）

A、 $24 °$ B、 $30 °$ C、 $36 °$ D、 $60 °$

查看试题解析
9. 如图，已知 $A B$ 是 $⊙ O$ 的直径，弦 $C D ⊥ A B$ ，垂足为 $E, ∠ A C D = 22.5 °, A B = 4$ ，则 $C D$ 的长为（）

A、 $2 \sqrt{2}$ B、5 C、 $4 \sqrt{2}$ D、 $2 \sqrt{6}$

查看试题解析
10. 函数 $y = | a x^{2} + b x + c | (a > 0, b^{2} - 4 a c > 0)$ 的图象是由函数 $y = a x^{2} + b x + c (a > 0, b^{2} - 4 a c > 0)$ 的图象x轴上方部分不变，下方部分沿x轴向上翻折而成，如图所示，则下列结论正确的是（）
① $2 a + b = 0$ ；② $c = 3$ ；③ $a b c > 0$ ；④图象向上平移2个单位后与直线 $y = 5$ 有3个交点．

A、①② B、①③④ C、②③④ D、①③

查看试题解析

二、填空题（共5题，每题3分，共15分）

11. 若使代数式 $\sqrt{2 - x}$ 有意义，则 $x$ 的取值范围是．

查看试题解析
12. 《水浒传》是中学生必读名著之一，王林将水浒人物宋江和李逵的画像及其绰号制成4张无差别卡片（除图案和文字不同外，其他完全相同）．将卡片背面朝上洗匀，从中随机抽取两张，则抽取的卡片人物画像与绰号完全对应的概率是．

查看试题解析
13. 如图，学校教学楼 $A B$ 的后面有一栋宿舍楼 $C D$ ，当光线与地面的夹角是 $25 °$ 时，教学楼在宿舍楼的墙上留下高 $3 m$ 的影子 $C E$ ，而当光线与地而夹角是 $45 °$ 时，教学楼顶 $A$ 在地面上的影子 $F$ 与墙角 $C$ 有 $20 m$ 的距离（ $B, F, C$ 在一条直线上），则教学楼 $A B$ 的高度为 $m$ ．（结果精确到 $1 m$ ，参考数据： $s i n 25 ° \approx 0.42, c o s 25 ° \approx 0.91, s i n 25 ° \approx 0.42$ ．）

查看试题解析
14. 我国南宋数学家杨辉在所著的《详解九章算术》一书中，用如图的三角形给出了 $(a + b)^{n}$ （ $n$ 为正整数）的展开式（按 $a$ 的次数由大到小的顺序）的系数规律，例如：此三角形中第3行的3个数1、2、1，恰好对应着 $(a + b)^{2} = a^{2} + 2 a b + b^{2}$ 展开式中的各项的系数，则 $(a + b)^{2024}$ 的展开式中含 $a^{2023}$ 项的系数是．

查看试题解析
15. 如图，在 $R t △ A B C$ 中， $∠ A C B = 90 °$ ， $∠ A B C = 30 °$ ， $A C = 4$ ，按下列步骤作图：①在 $A C$ 和 $A B$ 上分别截取 $A D$ 、 $A E$ ，使 $A D = A E$ ． ②分别以点D和点E为圆心，以大于 $\frac{1}{2} D E$ 的长为半径作弧，两弧在 $∠ B A C$ 内交于点M ． ③作射线 $A M$ 交 $B C$ 于点F ．若点P是线段 $A F$ 上的一个动点，连接 $C P$ ，则 $C P + \frac{1}{2} A P$ 的最小值是．

查看试题解析

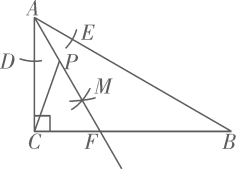
三、解答题（共9题，共75分．解答应写出文字说明、证明过程或演算步骤）

16. $| - 2024 | + π^{0} - {(\frac{1}{6})}^{- 1} + \sqrt{16} + t a n 45 °$

查看试题解析
17. 如图，在矩形 $A B C D$ 中，点 $F$ 在 $C B$ 的延长线上， $A F = A C$ ，求证：四边形 $A F B D$ 是平行四边形。

查看试题解析
18. 轮船在顺水中航行80千米所需的时间和逆水中航行60千米所需的时间相同．已知轮船在静水中的速度是21千米/时，求水流的速度．

查看试题解析
19. 2023年以来，高新区把垃圾分类纳入积分，建立文明账户，市民以行动换积分，以积分转习惯．区政府为了解9月份甲、乙两个社区垃圾分类换积分的情况，从甲、乙两个社区各抽取10人，记录下他们的积分（单位：分），并进行整理和分析（积分用x表示，共分为四组： $A : x < 70, B : 70 \leq x < 80, C : 80 \leq x < 90, D : 90 \leq x \leq 100$ ），下面给出了部分信息：
甲社区10人的积分： $47, 56, 68, 71, 83, 83, 85, 90, 91, 94$
乙社区10人的积分在 $C$ 组中的分数为： $81, 83, 84, 84$
两组数据的平均数、中位数、众数如下表
社区
平均数
中位数
众数
甲
76.8
83
b
乙
76.8
a
84
根据以上信息，解答下列问题：

(1)、填空： $a =$ ， $b =$ ， $m =$ ；

(2)、根据以上数据，你认为 ▲ 社区在此次垃圾分类换积分活动中表现更好．请说明理由（一条理由即可）；

(3)、若9月份甲社区有620人参与活动，乙社区有480人参与活动，请估计该月甲、乙两个社区积分在 $C$ 组的一共有多少人？

查看试题解析
20. 如图，反比例函数 $y = \frac{k}{x} (x < 0)$ 与一次函数 $y = - 2 x + m$ 的图象交于点 $A (- 1, 4), B C ⊥ y$ 轴于点 $D$ ，分别交反比例函数与一次函数的图象于点 $B, C$ ．

(1)、求反比例函数 $y = \frac{k}{x}$ 与一次函数 $y = - 2 x + m$ 的表达式；

(2)、当 $O D = 1$ 时，求线段 $B C$ 的长．

(3)、直接写出上 $\frac{k}{x} \geq - 2 x + m$ 的解集．

查看试题解析
21. 如图， $△ A B C$ 是 $⊙ O$ 的内接三角形，过点 $A$ 的直线与 $B C$ 的延长线交于点 $F$ ， $∠ F A C = ∠ B$ ．

(1)、求证： $A F$ 是 $⊙ O$ 的切线；

(2)、若 $A C = 3, t a n B = \frac{1}{3}$ ，求 $⊙ O$ 的半径．

查看试题解析
22. 某商店出售一款商品，经市场调查反映，该商品的日销售量 $y$ （件）与销售单价 $x$ （元）之间满足一次函数关系，关于该商品的销售单价，日销售量，日销售利润的部分对应数据如表：
销售单价 $x$ （元）
75
78
82
日销售量 $y$ （件）
150
120
80
日销售利润 $w$ （元）
5250
$a$
3360

(1)、根据以上信息，求 $y$ 关于 $x$ 的函数关系式．

(2)、①该产品的成本单价是 ▲ 元， $a$ 值是 ▲ ．
②求该商品日销售利润的最大值．

(3)、由于某种原因，该商品进价降低了 $m$ 元/件 $(m > 0)$ ，该商店在今后的销售中，商店规定该商品的销售单价不低于68元，日销售量与销售单价仍然满足（1）中的函数关系，若日销售最大利润是6600元，求 $m$ 的值．

查看试题解析
23. 如图

(1)、【问题发现】
如图1，在正方形 $A B C D$ 中， $E$ 为对角线 $A C$ 上的动点，过点 $B$ 作 $B E$ 的垂线，过点 $C$ 作 $A C$ 的垂线，两条垂线交于点 $F$ ，连接 $E F$ ，求证： $B E = B F$ ．

(2)、【类比探究】
如图2，在矩形 $A B C D$ 中， $E$ 为对角线 $A C$ 上的动点，过点 $B$ 作 $B E$ 的垂线，过点 $C$ 作 $A C$ 的垂线，两条垂线交于点 $F$ ，且 $∠ A C B = 60 °$ ，连接 $E F$ ，求 $\frac{C F}{A E}$ 的值．

(3)、【拓展延伸】
如图3，在（2）的条件下，将 $E$ 改为直线 $A C$ 上的动点，其余条件不变，取线段 $E F$ 的中点 $M$ ，连接 $B M, C M$ ．若 $A B = 2 \sqrt{3}$ ，则当 $△ C B M$ 是直角三角形时，求 $C F$ 的长．

查看试题解析
24. 如图，在平面直角坐标系中，抛物线 $y = - \frac{1}{4} x^{2} + b x + c$ （ $b 、 c$ 是常数）经过点 $A (2, 0)$ 点 $B (0, 3)$ ．点 $P$ 在抛物线上，其横坐标为 $m$ ．

(1)、求此抛物线解析式；

(2)、当点 $P$ 在 $x$ 轴上方时，结合图象，直接写出 $x$ 的取值范围；

(3)、若此抛物线在点右 $P$ 侧部分（包括点 $P$ ）的最高点的纵坐标为 $- 2 - m$ ．
①求 $m$ 的值．
②以 $P A$ 为边作等腰直角三角形 $P A Q$ ，当点 $Q$ 在此抛物线的对称轴上时，直接写出点 $Q$ 的坐标．

查看试题解析

销售单价 $x$ （元）	75	78	82
日销售量 $y$ （件）	150	120	80
日销售利润 $w$ （元）	5250	$a$	3360

社区	平均数	中位数	众数
甲	76.8	83	b
乙	76.8	a	84