湖北省阳新县城区四校2024年九年级第一次模拟考试数学试卷
试卷更新日期:2024-04-26 类型:中考模拟
一、选择题(共10小题,每小题3分,共30分)
-
1. 有四包真空小包装零食,每包以标准克数(100克)为基准,超过的克数记作正数,不足的克数记作负数,以下数据是记录结果,其中表示实际克数最接近标准克数的是( )A、﹣1 B、﹣2 C、+3 D、﹣42. 下列运算结果等于的是( )A、 B、 C、 D、3. 1月9日,中国国家铁路集团有限公司发布数据称,2023年全年,国家铁路完成旅客发送量36.8亿人次,高峰日发送旅客突破2000万人次,全年和高峰日旅客发送量均创历史新高,其中数据“36.8亿”用科学记数法表示为( )A、 B、 C、 D、4. 如图,将直尺与角的三角尺叠放在一起,若 , 则的大小是( )
 A、 B、 C、 D、5. 下列说法中正确的是( )A、一组数据2、3、3、5、5、6,这组数据中没有众数 B、袋中有10个蓝球,1个绿球,随机摸出一个球是绿球的概率是0.1 C、对湛江市区全年水质调查,适合用全面调查 D、画出一个三角形,其内角和是180度为必然事件6. 不等式组 的解集,在数轴上表示正确的是( )A、
A、 B、 C、 D、5. 下列说法中正确的是( )A、一组数据2、3、3、5、5、6,这组数据中没有众数 B、袋中有10个蓝球,1个绿球,随机摸出一个球是绿球的概率是0.1 C、对湛江市区全年水质调查,适合用全面调查 D、画出一个三角形,其内角和是180度为必然事件6. 不等式组 的解集,在数轴上表示正确的是( )A、 B、
B、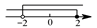 C、
C、 D、
D、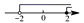 7. 反比例函数的图象经过点 , 则下列说法错误的是( )A、 B、函数图象分布在第二、四象限 C、函数图象关于原点中心对称 D、当时,y随x的增大而减小8. 如图,PA , PB是⊙O的切线,A , B为切点,AC是⊙O的直径,∠BAC=28°,则∠P的度数是( )
7. 反比例函数的图象经过点 , 则下列说法错误的是( )A、 B、函数图象分布在第二、四象限 C、函数图象关于原点中心对称 D、当时,y随x的增大而减小8. 如图,PA , PB是⊙O的切线,A , B为切点,AC是⊙O的直径,∠BAC=28°,则∠P的度数是( ) A、50° B、58° C、56° D、55°9. 在平面直角坐标系中,点A的坐标为 , 轴,且 , 则点B的坐标为( )A、 B、 C、或 D、或10. 如图,已知二次函数的图象与x轴交于点 , 与y轴的交点B在和之间(不包括这两点),对称轴为直线 . 下列结论:①;②;③;④;⑤ . 其中含所有正确结论的选项是( )
A、50° B、58° C、56° D、55°9. 在平面直角坐标系中,点A的坐标为 , 轴,且 , 则点B的坐标为( )A、 B、 C、或 D、或10. 如图,已知二次函数的图象与x轴交于点 , 与y轴的交点B在和之间(不包括这两点),对称轴为直线 . 下列结论:①;②;③;④;⑤ . 其中含所有正确结论的选项是( ) A、①③④ B、①③⑤ C、②④⑤ D、①③④⑤
A、①③④ B、①③⑤ C、②④⑤ D、①③④⑤二、填空题(本大题共有5个小题,每小题3分,共15分.不要求写出解答过程,请把答案直接填写在答题卷相应位置上)
-
11. 计算: .12. 某种服装原价每件80元,经两次降价,现售价每件64.8元,这种服装平均每次降价的百分率是.13. 关于的一元一次不等式组的两个不等式的解集在数轴上表示如图,则的值为 .
 14. 小明学习相交直线时发现:3条直线两两相交最多有3个交点,4条直线两两相交最多有6个交点,按照这样的规律,(1)、5条直线两两相交最多有个交点;(2)、n条直线两两相交最多有个交点.(用含有字母n的式子表示,)15. 在△ABC中, , , 点D是边上一动点,将△ACD沿直线翻折,使点A落在点E处,连接交于点F(所给图形仅仅是示意图).当△DEF是直角三角形时, .
14. 小明学习相交直线时发现:3条直线两两相交最多有3个交点,4条直线两两相交最多有6个交点,按照这样的规律,(1)、5条直线两两相交最多有个交点;(2)、n条直线两两相交最多有个交点.(用含有字母n的式子表示,)15. 在△ABC中, , , 点D是边上一动点,将△ACD沿直线翻折,使点A落在点E处,连接交于点F(所给图形仅仅是示意图).当△DEF是直角三角形时, .
三、解答题(共9题,共75分,解答应写出文字说明、证明过程或演算步骤)
-
16. 先化简,再求值 ,其中 , .17. 如图,在□ABCD中,对角线AC , BD相交于点O , 且OA=OB=5,AB=6,求□ABCD的面积.
 18. 甲、乙两座城市的中心火车站A , B两站相距360km . 一列动车与一列特快列车分别从A , B两站同时出发相向而行,动车的平均速度比特快列车快54km/h , 当动车到达B站时,特快列车恰好到达距离A站135km处的C站.求动车和特快列车的平均速度各是多少?
18. 甲、乙两座城市的中心火车站A , B两站相距360km . 一列动车与一列特快列车分别从A , B两站同时出发相向而行,动车的平均速度比特快列车快54km/h , 当动车到达B站时,特快列车恰好到达距离A站135km处的C站.求动车和特快列车的平均速度各是多少?
19. 如图,AE∥BF,AC平分∠BAE,且交BF于点C.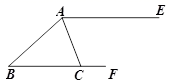 (1)、作∠ABF的平分线交AE于点D(尺规作图,保留痕迹,不写作法);(2)、根据(1)中作图,连接CD,求证:四边形ABCD是菱形.20. 如图,已知反比例函数的图象与直线相交于 , 两点.
(1)、作∠ABF的平分线交AE于点D(尺规作图,保留痕迹,不写作法);(2)、根据(1)中作图,连接CD,求证:四边形ABCD是菱形.20. 如图,已知反比例函数的图象与直线相交于 , 两点. (1)、求反比例函数与一次函数的解析式;(2)、求△AOB的面积;(3)、直接写出当时,对应的x的取值范围.21. 如图,在Rt△ABC中,∠C=90°,AD平分∠BAC交BC于点D,O为AB上一点,经过点A、D的⊙O分别交边AB、AC于点E、F.
(1)、求反比例函数与一次函数的解析式;(2)、求△AOB的面积;(3)、直接写出当时,对应的x的取值范围.21. 如图,在Rt△ABC中,∠C=90°,AD平分∠BAC交BC于点D,O为AB上一点,经过点A、D的⊙O分别交边AB、AC于点E、F. (1)、求证:BC是⊙O的切线;(2)、若 , , 求阴影部分的面积.22. 有一种葡萄:从树上摘下后不保鲜最多只能存放一周,如果放在冷藏室,可以延长保鲜时间,但每天仍有一定数量的葡萄变质,假设保鲜期内的重量基本保持不变,现有一位个体户,按市场价收购了这种葡萄200千克放在冷藏室内,此时市场价为每千克2元,据测算,此后每千克鲜葡萄的市场价格每天可以上涨0.2元,但是,存放一天需各种费用20元,平均每天还有1千克葡萄变质丢弃.(1)、存放x天后将鲜葡萄一次性出售,设鲜葡萄的销售金额为y元,写出y关于x的函数关系式;(2)、为了使鲜葡萄的销售金额为760元,又为了尽早清空冷藏室,则需要在几天后一次性出售完;(3)、问个体户将这批葡萄存放多少天后一次性出售,可获得最大利润?最大利润是多少?(本题不要求写出自变量x的取值范围)23. 在矩形中,(k为常数), 点P是对角线BD上一动点(不与B,D重合),将射线PA绕点P逆时针旋转90°与射线CB交于点E,连接AE.
(1)、求证:BC是⊙O的切线;(2)、若 , , 求阴影部分的面积.22. 有一种葡萄:从树上摘下后不保鲜最多只能存放一周,如果放在冷藏室,可以延长保鲜时间,但每天仍有一定数量的葡萄变质,假设保鲜期内的重量基本保持不变,现有一位个体户,按市场价收购了这种葡萄200千克放在冷藏室内,此时市场价为每千克2元,据测算,此后每千克鲜葡萄的市场价格每天可以上涨0.2元,但是,存放一天需各种费用20元,平均每天还有1千克葡萄变质丢弃.(1)、存放x天后将鲜葡萄一次性出售,设鲜葡萄的销售金额为y元,写出y关于x的函数关系式;(2)、为了使鲜葡萄的销售金额为760元,又为了尽早清空冷藏室,则需要在几天后一次性出售完;(3)、问个体户将这批葡萄存放多少天后一次性出售,可获得最大利润?最大利润是多少?(本题不要求写出自变量x的取值范围)23. 在矩形中,(k为常数), 点P是对角线BD上一动点(不与B,D重合),将射线PA绕点P逆时针旋转90°与射线CB交于点E,连接AE. (1)、特例发现:如图1,当k=1时,将点P移动到对角线交点处,可发现点E与点B重合,则 , ;当点P移动到其它位置时,的大小(填“改变”或“不变”);(2)、类比探究:如图2,若k≠1时,当k的值确定时,请探究∠AEP的大小是否会随着点P的移动而发生变化,并说明理由;(3)、拓展应用:当k≠1时,如图2,连接PC,若PC⊥BD,AE∥PC,PC=2,求AP的长.24. 如图①,直线与x轴、y轴分别交于A,B两点,抛物线与y轴交于点 , 与x轴正半轴交于点 , 设M是点C,D间抛物线上的一点(包括端点),其横坐标为m.
(1)、特例发现:如图1,当k=1时,将点P移动到对角线交点处,可发现点E与点B重合,则 , ;当点P移动到其它位置时,的大小(填“改变”或“不变”);(2)、类比探究:如图2,若k≠1时,当k的值确定时,请探究∠AEP的大小是否会随着点P的移动而发生变化,并说明理由;(3)、拓展应用:当k≠1时,如图2,连接PC,若PC⊥BD,AE∥PC,PC=2,求AP的长.24. 如图①,直线与x轴、y轴分别交于A,B两点,抛物线与y轴交于点 , 与x轴正半轴交于点 , 设M是点C,D间抛物线上的一点(包括端点),其横坐标为m. (1)、求抛物线的解析式:(2)、当m为何值时,面积S取得最大值?请说明理由;(3)、如图②,连接 , 抛物线的对称轴上是否存在点Q,使得 , 如果存在,请求出点Q的坐标,不存在,请说明理由.
(1)、求抛物线的解析式:(2)、当m为何值时,面积S取得最大值?请说明理由;(3)、如图②,连接 , 抛物线的对称轴上是否存在点Q,使得 , 如果存在,请求出点Q的坐标,不存在,请说明理由.