湖北省恩施州宣恩县2024年中考一模数学试题
试卷更新日期:2024-04-26 类型:中考模拟
一、选择题(本大题共有10个小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的,请将选择项前的字母代号填涂在答题卷相应位置上)
-
1. 2024的相反数是( )A、 B、2024 C、 D、2. 下列4个图形中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列计算正确的是( )A、 B、 C、 D、4. 如图,将直尺与角的三角尺叠放在一起,若 , 则的大小是( )
3. 下列计算正确的是( )A、 B、 C、 D、4. 如图,将直尺与角的三角尺叠放在一起,若 , 则的大小是( ) A、 B、 C、 D、5. 中国古代数学有着辉煌的成就,《周髀算经》、《算学启蒙》、《测圆海镜》、《四元玉鉴》是我国古代数学的重要文献.某中学拟从这4部数学名著中选择2部作为校本课程“数学文化”的学习内容,恰好选中《算学启蒙》的概率是( )A、 B、 C、 D、6. 用5个完全相同的小正方体组成如图所示的立体图形,它的左视图是( )
A、 B、 C、 D、5. 中国古代数学有着辉煌的成就,《周髀算经》、《算学启蒙》、《测圆海镜》、《四元玉鉴》是我国古代数学的重要文献.某中学拟从这4部数学名著中选择2部作为校本课程“数学文化”的学习内容,恰好选中《算学启蒙》的概率是( )A、 B、 C、 D、6. 用5个完全相同的小正方体组成如图所示的立体图形,它的左视图是( )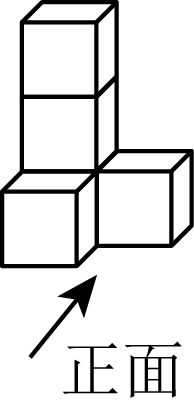 A、
A、 B、
B、 C、
C、 D、
D、 7. 若关于x的一元二次方程的两个实数根分别为 , 则的值为( )A、2 B、3 C、 D、8. 如图,PA , PB是⊙O的切线,A , B为切点,AC是⊙O的直径,∠BAC=28°,则∠P的度数是( )
7. 若关于x的一元二次方程的两个实数根分别为 , 则的值为( )A、2 B、3 C、 D、8. 如图,PA , PB是⊙O的切线,A , B为切点,AC是⊙O的直径,∠BAC=28°,则∠P的度数是( ) A、50° B、58° C、56° D、55°9. 如图,在平面直角坐标系中,已知正方形的顶点A的坐标为 , 则点C的坐标为( )
A、50° B、58° C、56° D、55°9. 如图,在平面直角坐标系中,已知正方形的顶点A的坐标为 , 则点C的坐标为( ) A、 B、 C、 D、10. 如图,已知二次函数的图象与x轴交于点 , 与y轴的交点B在和之间(不包括这两点),对称轴为直线 . 下列结论:①;②;③;④;⑤ . 其中含所有正确结论的选项是( )
A、 B、 C、 D、10. 如图,已知二次函数的图象与x轴交于点 , 与y轴的交点B在和之间(不包括这两点),对称轴为直线 . 下列结论:①;②;③;④;⑤ . 其中含所有正确结论的选项是( ) A、①③④ B、①③⑤ C、②④⑤ D、①③④⑤
A、①③④ B、①③⑤ C、②④⑤ D、①③④⑤二、填空题(本大题共有5个小题,每小题3分,共15分.不要求写出解答过程,请把答案直接填写在答题卷相应位置上)
-
11. 因式分解的结果是 .12. 若一组数据的平均数为4,则的平均数为 .13. 关于的一元一次不等式组的两个不等式的解集在数轴上表示如图,则的值为 .
 14. 图1是临安区一地铁站入口的双翼闸机,双翼展开时示意图如图2所示,它是一个轴对称图形, , 则双翼边缘端点C与D之间的距离为 (用含α的三角函数表示).
14. 图1是临安区一地铁站入口的双翼闸机,双翼展开时示意图如图2所示,它是一个轴对称图形, , 则双翼边缘端点C与D之间的距离为 (用含α的三角函数表示). 15. 已知整数 , 满足下列条件: , …,依此类推,则的值为 .
15. 已知整数 , 满足下列条件: , …,依此类推,则的值为 .三、解答题(本大题共有9个小题,共75分.请在答题卷指定区域内作答,解答时应写出文字说明.证明过程或演算步骤)
-
16. 计算: .17. 先化简,再求值: , 其中 .18. 如图,矩形ABCD的对角线相交于点O,DE//AC,CE//BD,
求证:四边形OCED是菱形.
 19. 为落实“双减”政策,优化作业管理,某中学从全体学生中随机抽取部分学生,调查他们每天完成书面作业的时间t(单位:分钟)按照完成时间分成五组:A组“t≤45”,B组“45<t≤60”,C组“60<t≤75”,D组“75<t≤75”,E组“t>90”将收集的数据整理后,绘制成如下两幅不完整的统计图.
19. 为落实“双减”政策,优化作业管理,某中学从全体学生中随机抽取部分学生,调查他们每天完成书面作业的时间t(单位:分钟)按照完成时间分成五组:A组“t≤45”,B组“45<t≤60”,C组“60<t≤75”,D组“75<t≤75”,E组“t>90”将收集的数据整理后,绘制成如下两幅不完整的统计图.根据以上信息,解答下列问题:
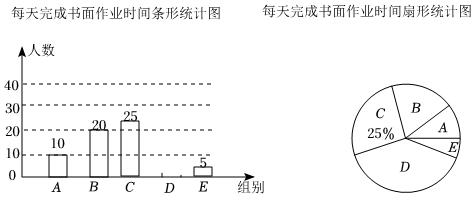 (1)、这次调查的样本容量是 ▲ , 请补全条形统计图;(2)、在扇形统计图中,组的圆心角是度,本次调查数据的中位数落在组内;(3)、若该校有1800名学生,请你估计该校每天完成书面作业不超过90分钟的学生人数.20. 如图,已知反比例函数的图象与直线相交于 , 两点.
(1)、这次调查的样本容量是 ▲ , 请补全条形统计图;(2)、在扇形统计图中,组的圆心角是度,本次调查数据的中位数落在组内;(3)、若该校有1800名学生,请你估计该校每天完成书面作业不超过90分钟的学生人数.20. 如图,已知反比例函数的图象与直线相交于 , 两点. (1)、求反比例函数与一次函数的解析式;(2)、求△AOB的面积;(3)、直接写出当时,对应的x的取值范围.21. 已知四边形ABCD内接于⊙O,连接AC,BD,若BD是⊙O的直径,AC平分∠BCD,过A作∠BAE=∠BDA,AE与CB的延长线交于点E.
(1)、求反比例函数与一次函数的解析式;(2)、求△AOB的面积;(3)、直接写出当时,对应的x的取值范围.21. 已知四边形ABCD内接于⊙O,连接AC,BD,若BD是⊙O的直径,AC平分∠BCD,过A作∠BAE=∠BDA,AE与CB的延长线交于点E. (1)、求证:AE是⊙O的切线;(2)、若 , , 求图中阴影部分的面积(结果保留).22. 某超市销售一种进价为18元/千克的商品,经市场调查后发现,每天的销售量y(千克)与销售单价x(元/千克)有如下表所示的关系:
(1)、求证:AE是⊙O的切线;(2)、若 , , 求图中阴影部分的面积(结果保留).22. 某超市销售一种进价为18元/千克的商品,经市场调查后发现,每天的销售量y(千克)与销售单价x(元/千克)有如下表所示的关系:销售单价x(元/千克)
…
20
22.5
25
37.5
40
…
销售量y(千克)
…
30
27.5
25
12.5
10
…
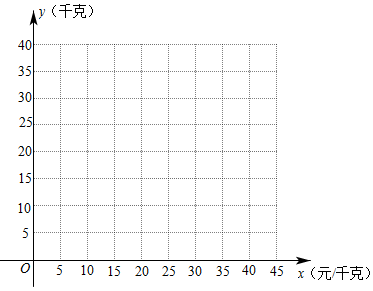 (1)、根据表中的数据在下图中描点 , 并用平滑曲线连接这些点,请用所学知识求出y关于x的函数关系式;(2)、设该超市每天销售这种商品的利润为w(元)(不计其它成本),
(1)、根据表中的数据在下图中描点 , 并用平滑曲线连接这些点,请用所学知识求出y关于x的函数关系式;(2)、设该超市每天销售这种商品的利润为w(元)(不计其它成本),①求出w关于x的函数关系式,并求出获得最大利润时,销售单价为多少;
②超市本着“尽量让顾客享受实惠”的销售原则,求(元)时的销售单价.
23. 在中, . (1)、特例证明:如图1,点D,E分别在线段上, , 求证:;(2)、探索发现:将图1中的绕点C逆时针旋转()到图2位置,(1)中的结论还成立吗?若成立,请证明;若不成立,请说明理由;(3)、拓展运用:如图3,点D在内部,当时,若 , , , 求线段的长(直接写出答案).24. 如图①,直线与x轴、y轴分别交于A,B两点,抛物线与y轴交于点 , 与x轴正半轴交于点 , 设M是点C,D间抛物线上的一点(包括端点),其横坐标为m.
(1)、特例证明:如图1,点D,E分别在线段上, , 求证:;(2)、探索发现:将图1中的绕点C逆时针旋转()到图2位置,(1)中的结论还成立吗?若成立,请证明;若不成立,请说明理由;(3)、拓展运用:如图3,点D在内部,当时,若 , , , 求线段的长(直接写出答案).24. 如图①,直线与x轴、y轴分别交于A,B两点,抛物线与y轴交于点 , 与x轴正半轴交于点 , 设M是点C,D间抛物线上的一点(包括端点),其横坐标为m. (1)、求抛物线的解析式:(2)、当m为何值时,面积S取得最大值?请说明理由;(3)、如图②,连接 , 抛物线的对称轴上是否存在点Q,使得 , 如果存在,请求出点Q的坐标,不存在,请说明理由.
(1)、求抛物线的解析式:(2)、当m为何值时,面积S取得最大值?请说明理由;(3)、如图②,连接 , 抛物线的对称轴上是否存在点Q,使得 , 如果存在,请求出点Q的坐标,不存在,请说明理由.