湖南省邵阳市新邵县小塘镇2024年中考一模数学试题

试卷更新日期：2024-04-25 类型：中考模拟

进入出卷网下载

一、选择题（本大题共10个小题，每小题3分，共30分，在每小题给出的四个选项中，只有一项是符合题目要求的；请将你认为正确的选项填涂到答题卡上）

1. -2024的倒数是（）

A、2024 B、-2024 C、 $\frac{1}{2024}$ D、 $- \frac{1}{2024}$

查看试题解析
2. 火星是太阳系九大行星之一，火星的半径约为3395000米，数3395000用科学记数法表示为（）

A、 $33.95 \times 1 0^{5}$ B、 $3.395 \times 1 0^{5}$ C、 $3.395 \times 1 0^{6}$ D、 $0.3395 \times 1 0^{7}$

查看试题解析
3. 下列运算正确的是（）

A、 $(x + 2)^{2} = x^{2} + 4$ B、 $a^{2} \cdot a^{4} = a^{8}$ C、 ${(2 x^{3})}^{2} = 4 x^{6}$ D、 $2 x^{2} + 3 x^{2} = 5 x^{4}$

查看试题解析
4. 如图是由五个相同的正方体搭成的几何体，这个几何体的主视图是（）

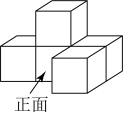A、 B、 C、 D、

查看试题解析
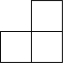5. 二次函数 $y = - (x + 1)^{2} + 2$ 图象的顶点所在的象限是（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
6. 县林业部门考察银杏树苗在一定条件下移植的成活率，统计银杏树苗移植成活的相关数据如下表所示：
移植的棵数 $a$
100
300
600
1000
7000
15000
成活的棵数 $b$
84
279
505
847
6337
13581
成活的频率 $\frac{b}{a}$
0.84
0.93
0.842
0.847
0.905
0.905
根据表中的信息，估计银杏树苗在一定条件下移植成活的概率为（精确到0.1）

A、0.905 B、0.90 C、0.9 D、0.8

查看试题解析
7. 如图，在平面直角坐标系中， $△ O A B$ 的顶点为 $O (0 ， 0)$ ， $A (12 ， 9)$ ， $B (9 ， 0)$ ．以点 $O$ 为位似中心，在第三象限内作与 $△ O A B$ 的位似比为 $\frac{1}{3}$ 的位似图形 $△ O C D$ ，则点 $C$ 的坐标为（）

A、 $(- 3 ， - 3)$ B、 $(- 4 ， - 3)$ C、 $(- 3 ， - 4)$ D、 $(- 6 ， - 3)$

查看试题解析
8. 湖湘饮食文化源远流长，“大碗米粉”是湖南地方特色美食之一.图②是从正面看到的一个“大碗”（图①）的形状示意图. $\overset{⌢}{A B}$ 是 $⊙ O$ 的一部分， $D$ 是 $\overset{⌢}{A B}$ 的中点，连接 $O D$ ，与弦 $A B$ 交于点 $C$ ，连接 $O A$ ， $O B$ .已知 $A B = 24 c m$ ，碗深 $C D = 8 c m$ ，则 $⊙ O$ 的半径 $O A$ 为（）

A、 $13 c m$ B、 $16 c m$ C、 $17 c m$ D、 $26 c m$

查看试题解析
9. 《九章算术》之“粟米篇”中记载了中国古代的“粟米之法”：“粟率五十，粝米三十……”（粟指带壳的谷子，粝米指糙米），其意为“50单位的粟，可换得30单位的粝米……”.问题：有3斗的粟（1斗＝10升），若按照此“粟米之法”，则可以换得的粝米为（）

A、1.8升 B、16升 C、18升 D、50升

查看试题解析
10. 如图，在平面直角坐标系中，O为原点，OA＝OB＝3 $\sqrt{5}$ ，点C为平面内一动点，BC＝ $\frac{3}{2}$ ，连接AC ，点M是线段AC上的一点，且满足CM：MA＝1：2．当线段OM取最大值时，点M的坐标是（　　）

A、 $(\frac{3}{5} ， \frac{6}{5})$ B、 $(\frac{3}{5} \sqrt{5} ， \frac{6}{5} \sqrt{5})$ C、 $(\frac{6}{5} ， \frac{12}{5})$ D、 $(\frac{6}{5} \sqrt{5} ， \frac{12}{5} \sqrt{5})$

查看试题解析

二、填空题（本大题共8个小题，每小题3分，共24分；请将答案填在答题卡的答案栏内）

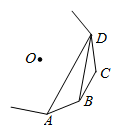
11. 在平面直角坐标系中，若点 $P (2 ， - 1)$ 与点 $Q (- 2 ， m)$ 关于原点对称，则 $m$ 的值是．

查看试题解析
12. 要使式子 $\sqrt{3 - x}$ 有意义，则x的取值范围是．

查看试题解析
13. 因式分解： $4 x^{2} - 1$ = .

查看试题解析
14. 如图， $A$ 、 $B$ 、 $C$ 、 $D$ 为一个正多边形的顶点， $O$ 为正多边形的中心，若 $∠ A D B = 20 °$ ，则这个正多边形的边数为.

查看试题解析
15. 已知一元二次方程 $x^{2} - 3 x + 1 = 0$ 的两个实数根分别为 $x_{1}$ 和 $x_{2}$ ，则 $x_{1} + x_{2} - x_{1} x_{2} =$ .

查看试题解析
16. 若菱形的两条对角线长分别为6和8，则该菱形的面积为．

查看试题解析
17. 如图，在网格中，每个小正方形的边长均为1，每个小正方形的顶点称为格点．点A、B、C三点都在格点上，则 $s i n ∠ A B C =$ ．

查看试题解析
18. 如图，平行于 $x$ 轴的直线与函数 $y = \frac{k_{1}}{x} (k_{1} > 0, x > 0)$ 和 $y = \frac{k_{2}}{x} (k_{2} > 0, x > 0)$ 的图象分别相交于 $A$ ， $B$ 点.点 $A$ 在点 $B$ 的右侧， $C$ 为 $x$ 轴上的一个动点，若 $△ A B C$ 的面积为4，则 $k_{1} - k_{2}$ 的值为.

查看试题解析

三、解答题（本大题共8个小题，第19-25题每题8分，第26题10分，共66分；解答应写出必要的文字说明、演算步骤或证明过程）

19. 计算： $(- 1)^{2024} + | \sqrt{3} - 2 | - {(\frac{1}{2})}^{- 1} + 2 s i n 60 °$ .

查看试题解析
20. 先化简，再求值： $(\frac{x^{2}}{x - 3} + \frac{9}{3 - x}) \div \frac{x + 3}{2 x}$ ，其中 $x = 1012$ .

查看试题解析
21. 如图，网格中每个小正方形的边长均为1，线段 $O A$ 的端点均在小正方形的格点上．

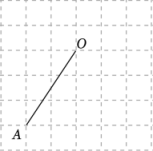(1)、画出线段 $O A$ 绕点 $O$ 顺时针旋转 $90 °$ 后得到的线段 $O B$ ；

(2)、在（1）的运动过程中，请计算出点 $A$ 绕点 $O$ 旋转到点 $B$ 所经过的路径长（结果保留 $π)$ ．

查看试题解析
22. 某学校根据《中小学生课后服务实施意见》，积极开展课后延时服务活动，提供了合唱、舞蹈、科创、书法、美术、课本剧、棋类等课程供学生自由选择.半学期后，该校为了解学生对课后延时服务的满意情况，随机对部分学生进行问卷调查，并将调查结果按照“A.满意；B.比较满意；C.基本满意；D.不满意”四个等级绘制成如图所示的两幅不完整统计图.
请根据图中信息，解答下列问题：

(1)、将条形统计图补充完整；

(2)、表示等级D的扇形的圆心角是°；

(3)、由于学校条件限制，“课本剧”课程仅剩下一个名额，而学生小华和小亮都想参加，他们决定采用抽纸牌的方法来确定，规则是：“将背面完全相同，正面分别标有数字1，2，3，4的四张牌洗匀后，背面朝上放置在桌面上，每人随机抽一次且一次只抽一张；一人抽后记下数字，将牌放回洗匀背面朝上放置在桌面上，再由另一人抽.若小华抽得的数字比小亮抽得的数字大，名额给小华，否则给小亮.”请用画树状图或列表的方法计算出小华和小亮获得该名额的概率，并说明这个规则对双方是否公平.

查看试题解析
23. 如图，已知在 $△ A B C$ 中， $∠ B A C = 90 °$ ， $D$ 是 $B C$ 的中点， $E$ 是 $A D$ 的中点，过点 $A$ 作 $A F ∥ B C$ 交 $B E$ 的延长线于点 $F$ ，连接 $C F$ .

(1)、求证：四边形 $A D C F$ 是菱形；

(2)、若 $A C = 8$ ，菱形 $A D C F$ 的面积为40，求 $A B$ 的长.

查看试题解析
24. 有甲、乙两种客车，2辆甲种客车与3辆乙种客车的总载客量为180人，1辆甲种客车与2辆乙种客车的总载客量为105人．

(1)、请问1辆甲种客车与1辆乙种客车的载客量分别为多少人？

(2)、某学校组织240名师生集体外出活动，拟租用甲、乙两种客车共6辆，一次将全部师生送到指定地点．若每辆甲种客车的租金为400元，每辆乙种客车的租金为280元，请给出最节省费用的租车方案，并求出最低费用．

查看试题解析
25. 如图，海中有一小岛 $P$ ，它周围8海里内有暗礁，渔船由西向东航行，在 $A$ 点测得小岛 $P$ 在北偏东 $60 °$ 方向上，航行12海里到达 $B$ 点，这时测得小岛 $P$ 在北偏东 $30 °$ 方向上.

(1)、求 $∠ A P B$ 的度数；

(2)、如果渔船不改变航线继续向东航行，有没有触礁的危险？

查看试题解析
26. 如图，在平面直角坐标系中，抛物线 $y = x^{2} + b x + c$ 与 $x$ 轴交于点 $A (2, 0)$ 和点 $B (4, 0)$ ，直线 $l$ 是对称轴.

(1)、求该抛物线的函数表达式；

(2)、在直线 $l$ 上是否存在点 $C$ ，使 $∠ A C B = 45 °$ ？若存在，求出点 $C$ 的坐标；若不存在，请说明理由；

(3)、 $P$ 为第一象限内抛物线上的一个动点，且在直线 $l$ 右侧，连接 $P A$ ， $P B$ ，过点 $P$ 作 $P M ⊥ l$ ，垂足为 $M$ ，以点 $M$ 为圆心、作半径为 $r$ 的圆， $P T$ 与 $⊙ M$ 相切，切点为 $T$ .若 $P T^{2} = S_{△ P A B}$ ，且 $⊙ M$ 不经过点 $(3, 3)$ ，求 $P M$ 长的取值范围.

查看试题解析

移植的棵数 $a$	100	300	600	1000	7000	15000
成活的棵数 $b$	84	279	505	847	6337	13581
成活的频率 $\frac{b}{a}$	0.84	0.93	0.842	0.847	0.905	0.905