湖南省永州市新田县2023-2024学年八年级下学期月考数学试题

试卷更新日期：2024-04-25 类型：月考试卷

进入出卷网下载

一、选择题（共10*4＝40分）

1. 如果 $\sqrt{(a - 2)^{2}} = 2 - a$ ，那么（）

A、 $a < 2$ B、 $a \leq 2$ C、 $a > 2$ D、 $a \geq 2$

查看试题解析
2. 若3、4、 $a$ 为勾股数，则a的值为（）

A、－5 B、5 C、－5或 $- \sqrt{7}$ D、5或 $\sqrt{7}$

查看试题解析
3. 下列关于一次函数y＝﹣2x＋2的图象的说法中，错误的是（）

A、函数图象经过第一、二、四象限 B、函数图象与x轴的交点坐标为（2，0） C、当x＞0时，y＜2 D、y的值随着x值的增大而减小

查看试题解析
4. 如图，台阶阶梯每一层高20cm，宽30cm，长50cm，一只蚂蚁从A点爬到B点，最短路程是（）

A、 $10 \sqrt{89}$ B、 $50 \sqrt{5}$ C、120 D、130

查看试题解析
5. 已知Rt△ABC中，∠C=90°，若a+b=14cm，c=10cm，则Rt△ABC的面积是( )

A、24cm² B、36cm² C、48cm² D、60cm²

查看试题解析
6. 如图，两张等宽的纸条交叉叠放在一起，若重合部分构成的四边形ABCD中，AB＝3，AC＝2，则四边形ABCD的面积为（）

A、 $4 \sqrt{2}$ B、 $6 \sqrt{2}$ C、 $8 \sqrt{2}$ D、5

查看试题解析
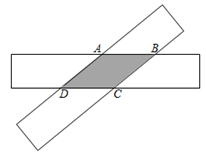7. 如果正整数a、b、c满足等式 $a^{2} + b^{2} = c^{2}$ ，那么正整数a、b、c叫做勾股数.某同学将自己探究勾股数的过程列成下表，观察表中每列数的规律，可知x+y的值为（）

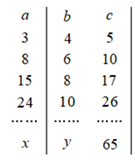A、47 B、62 C、79 D、98

查看试题解析
8.
如图，在矩形ABCD中，对角线AC，BD相交于点O，AE⊥BD，垂足为E，AE=3，ED=3BE，则AB的值为（　　）

A、6 B、5 C、 $2 \sqrt{3}$ D、 $3 \sqrt{3}$

查看试题解析
9. 我们知道，四边形具有不稳定性，如图，在平面直角坐标系中，边长为2的正方形 $A B C D$ 的边 $A B$ 在x轴上， $A B$ 的中点是坐标原点O，固定点A，B，把正方形沿箭头方向推，使点D落在y轴正半轴上点 $D^{'}$ 处，则点C的对应点 $C^{'}$ 的坐标为（）

A、 $(\sqrt{3}, 1)$ B、 $(2, 1)$ C、 $(1, \sqrt{3})$ D、 $(2, \sqrt{3})$

查看试题解析
10. 已知 $\frac{a}{b + c} = \frac{b}{a + c} = \frac{c}{a + b} = k$ ，则一次函数 $y = k x - 2 k$ 的图象一定过（）．

A、一、二、三象限 B、一、四象限 C、一、三、四象限 D、一、二象限

查看试题解析

二、填空题（共6*4＝24分）

11. 计算 $2 \sqrt{8} - 2 \sqrt{\frac{1}{2}}$ 的结果是．

查看试题解析
12. 已知点 $P (1 ， 2)$ 关于x轴的对称点为 $P^{'}$ ，且 $P^{'}$ 在直线 $y = k x + 3$ 上，则 $k =$ ．使代数式 $\sqrt{2 - x} + \frac{1}{| x | + 2}$ 有意义的x的取值范围是．

查看试题解析
13. $\sqrt{1 + \frac{1}{3}} = 2 \sqrt{\frac{1}{3}}$ ， $\sqrt{2 + \frac{1}{4}} = 3 \sqrt{\frac{1}{4}}$ ， $\sqrt{3 + \frac{1}{5}} = 4 \sqrt{\frac{1}{5}}$ ， …请你将发现的规律用含有自然数 $n (n \geq 1)$ 的等式表示出来为．

查看试题解析
14. 如图，两条宽度分别为2和4的长方形纸条交叉放置，重叠部分为四边形 $A B C D$ ，若 $A B \cdot B C = 100$ ，则四边形 $A B C D$ 的面积是

查看试题解析
15. 小高从家门口骑车去单位上班，先走平路到达点 $A$ ，再走上坡路到达点 $B$ ，最后走下坡路到达工作单位，所用的时间与路程的关系如图所示.下班后，如果他沿原路返回，且走平路、上坡路、下坡路的速度分别保持和去上班时一致，那么他从单位到家门口需要的时间是分钟.

查看试题解析
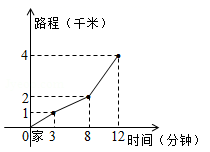16. 在如图所示的平面直角坐标系中，点P是直线y=x上的动点，A（2，0），B（6，0）是x轴上的两点，则PA+PB的最小值为．

查看试题解析

三、解答题

17. 计算： $(\sqrt{2} - 1) (\sqrt{2} + 1) + 2 \sqrt{8} - \frac{3}{\sqrt{2}}$ ．

查看试题解析
18. 已知：如图，直线y₁＝x+1在平面直角坐标系xOy中.

(1)、在平面直角坐标系xOy中画出y₂＝﹣2x+4的图象；

(2)、求y₁与y₂的交点坐标；

(3)、根据图象直接写出当y₁≥y₂时，x的取值范围.

查看试题解析
19. 如图，在四边形ABCD中，AD＝BC，E、F分别是边DC、AB的中点，FE的延长线分别与AD、BC的延长线交于点H、G，求证：∠AHF＝∠BGF．

查看试题解析
20. 定义：关于x的一次函数y＝ax+b与y＝bx+a（ab≠0）叫做一对交换函数，例如：一次函数y＝3x+4与y＝4x+3就是一对交换函数．

(1)、一次函数y＝2x﹣b的交换函数是；

(2)、当b≠﹣2时，（1）中两个函数图象交点的横坐标是；

(3)、若（1）中两个函数图象与y轴围成的三角形的面积为4，求b的值．

查看试题解析
21. 某校八年级学生开展踢毽子比赛活动，每班派5名学生参加，按团体总分多少排列名次，在规定时间内每人踢100个以上（含100）为优秀．下表是成绩最好的甲班和乙班5名学生的比赛数据（单位：个）：

1号
2号
3号
4号
5号
总数
甲班
120
118
130
109
123
600
乙班
109
120
115
139
117
600
经统计发现两班总数相等，此时有学生建议，可以通过考查数据中的其他信息作为参考．请你回答下列问题：

(1)、填空：甲班的优秀率为，乙班的优秀率为；

(2)、填空：甲班比赛数据的中位数为，乙班比赛数据的中位数为；

(3)、根据以上两条信息，你认为应该把冠军奖杯发给哪一个班级？简述你的理由．

查看试题解析
22. 已知一次函数y=-3x+3的图象分别与x轴，y轴交于A，B两点，点C（3，0）．

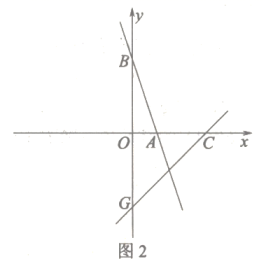(1)、如图1，点D与点C关于y轴对称，点E在线段BC上且到两坐标轴的距离相等，连接DE，交y轴于点F．求点E的坐标；

(2)、△AOB与△FOD是否全等，请说明理由；

(3)、如图2，点G与点B关于x轴对称，点P在直线GC上，若△ABP是等腰三角形，直接写出点P的坐标．

查看试题解析
23. 在平面直角坐标系中，已知点A（a，0），C（0，b）满足（a+1）²+ $\sqrt{b + 3}$ =0

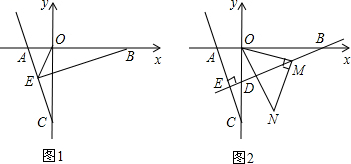(1)、直接写出：a= ， b=；

(2)、点B为x轴正半轴上一点，如图1，BE⊥AC于点E，交y轴于点D，连接OE，若OE平分∠AEB，求直线BE的解析式；

(3)、在（2）条件下，点M为直线BE上一动点，连OM，将线段OM逆时针旋转90°，如图2，点O的对应点为N，当点M的运动轨迹是一条直线l，请你求出这条直线l的解析式．

查看试题解析
24. 在平面直角坐标系中， $A (0, 8)$ 、 $C (8, 0)$ ，四边形 $A O C B$ 是正方形，点 $D (a, 0)$ 是 $x$ 轴正半轴上一动点， $∠ A D E = 90 °$ ， $D E$ 交正方形 $A O C B$ 外角平分线 $C E$ 于点 $E$ ．

(1)、如图1，当点 $D$ 是 $O C$ 的中点时，求证： $A D = D E$ ；

(2)、点 $D (a, 0)$ 在 $x$ 轴正半轴上运动，点 $P$ 在 $y$ 轴上．若四边形 $P D E B$ 为菱形，求直线 $P B$ 的解析式．

(3)、连 $A E$ ，点 $F$ 是 $A E$ 的中点，当点 $D$ 在 $x$ 轴正半轴上运动时，点 $F$ 随之而运动，点 $F$ 到 $C E$ 的距离是否为定值？若为定值，求出这个值；若不是定值，请说明理由．

查看试题解析
25. 如图，平面直角坐标系xOy中，正方形ABCD的边AB在x轴上，点O是AB的中点，直线l：y=kx+2k+4过定点D，交x轴于点P．

(1)、求正方形ABCD的边长；

(2)、如图1，在直线l上有一点N， $D N = \frac{1}{2} A B$ ，连接BN，点M为BN中点，连接AM，求线段AM的长度的最小值，并求出此时点N的坐标．

(3)、如图2，过点P作PE⊥DP交∠CBx的平分线于点E，点Q是直线AD上一点，四边形PQCE是否可能为菱形，如果能求出此时直线CQ的解析式，如果不能，则说明理由．

查看试题解析

	1号	2号	3号	4号	5号	总数
甲班	120	118	130	109	123	600
乙班	109	120	115	139	117	600