湖南省岳阳市汨罗市弼时片2023-2024学年九年级下学期月考数学试卷(3月份)
试卷更新日期:2024-04-25 类型:月考试卷
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
-
1. 的相反数是( )A、 B、 C、 D、2. 如图所示的几何体,其俯视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 3. 下列运算中,正确的是( )A、 B、 C、 D、4. 如图,已知 , , , 则的度数是( )
3. 下列运算中,正确的是( )A、 B、 C、 D、4. 如图,已知 , , , 则的度数是( ) A、 B、 C、 D、5. 某校名学生参加课外实践活动的时间分别为: , , , , , 单位:小时 , 这组数据的众数和中位数分别为( )A、和 B、和 C、和 D、和6. 下列命题中错误的是( )A、若 , 则 B、两直线平行,内错角相等 C、长度相等的弧所对圆周角相等 D、对顶角相等7. 九章算术是中国传统数学最重要的著作之一,书中记载:“今有人共买兔,人出七,盈十一;人出五,不足十三,问人数几何?”意思是:“有若干人共同出钱买兔,如果每人出七钱,那么多了十一钱;如果每人出五钱,那么少了十三钱问:共有几个人?”设有个人共同买鸡,依题意可列方程为( )A、 B、 C、 D、8. 如图,四边形内接于 , 弦 , 若 , 则的大小为( )
A、 B、 C、 D、5. 某校名学生参加课外实践活动的时间分别为: , , , , , 单位:小时 , 这组数据的众数和中位数分别为( )A、和 B、和 C、和 D、和6. 下列命题中错误的是( )A、若 , 则 B、两直线平行,内错角相等 C、长度相等的弧所对圆周角相等 D、对顶角相等7. 九章算术是中国传统数学最重要的著作之一,书中记载:“今有人共买兔,人出七,盈十一;人出五,不足十三,问人数几何?”意思是:“有若干人共同出钱买兔,如果每人出七钱,那么多了十一钱;如果每人出五钱,那么少了十三钱问:共有几个人?”设有个人共同买鸡,依题意可列方程为( )A、 B、 C、 D、8. 如图,四边形内接于 , 弦 , 若 , 则的大小为( ) A、 B、 C、 D、9. 如图,在中,半径弦于点 , 连接并延长交于点 , 连接 , 若 , , 则的长度为( )
A、 B、 C、 D、9. 如图,在中,半径弦于点 , 连接并延长交于点 , 连接 , 若 , , 则的长度为( ) A、 B、 C、 D、10. 如图,抛物线的顶点坐标为下列结论:;;关于的一元二次方程有两个不相等实数根;抛物线上有两点和 , 若 , 且 , 则其中正确的结论共有( )
A、 B、 C、 D、10. 如图,抛物线的顶点坐标为下列结论:;;关于的一元二次方程有两个不相等实数根;抛物线上有两点和 , 若 , 且 , 则其中正确的结论共有( ) A、个 B、个 C、个 D、个
A、个 B、个 C、个 D、个二、填空题:本题共8小题,每小题3分,共24分。
-
11. 要使分式有意义,则的取值范围为 .12. 光年是天文学中一种计量天体时空距离的长度单位,1光年约为9500000000000千米,将数9500000000000用科学记数法表示应为 .13. 解分式方程的解是 .14. 在一个不透明的袋子里,装有个红球和个白球,这些球除颜色外没有任何区别,现从这个袋子中随机摸出一个球,摸到红球的概率是 .15. 如图,在中, , 是边上的中点,若 , , 则的长为 .
 16. 若 , 是关于的一元二次方程的两个根,则代数式的值为 .17. 如图,由游客中心处修建通往百米观景长廊的两条栈道、 , 若 , , , 则游客中心到观景长廊的距离的长约为 结果精确到 , .
16. 若 , 是关于的一元二次方程的两个根,则代数式的值为 .17. 如图,由游客中心处修建通往百米观景长廊的两条栈道、 , 若 , , , 则游客中心到观景长廊的距离的长约为 结果精确到 , . 18. 如图,为外接圆的直径,点为的内心,连接并延长交于点 , 若 , 的直径为 , 则扇形的面积为 ;
18. 如图,为外接圆的直径,点为的内心,连接并延长交于点 , 若 , 的直径为 , 则扇形的面积为 ;若 , , 则 .

三、计算题:本大题共1小题,共6分。
-
19. 计算: .
四、解答题:本题共7小题,共60分。解答应写出文字说明,证明过程或演算步骤。
-
20. 先化简,再求值: , 其中 .21. 如图,在中, , 点 , , 分别是三边的中点.求证:四边形是菱形.
 22. 某学校为满足学生多样化学习需求,准备组建美术、劳动、科普、阅读四类社团.学校为了解学生的参与度,随机抽取了部分学生进行调查,将调查结果绘制成如图所示的不完整的统计图.请根据图中的信息,解答下列问题:
22. 某学校为满足学生多样化学习需求,准备组建美术、劳动、科普、阅读四类社团.学校为了解学生的参与度,随机抽取了部分学生进行调查,将调查结果绘制成如图所示的不完整的统计图.请根据图中的信息,解答下列问题: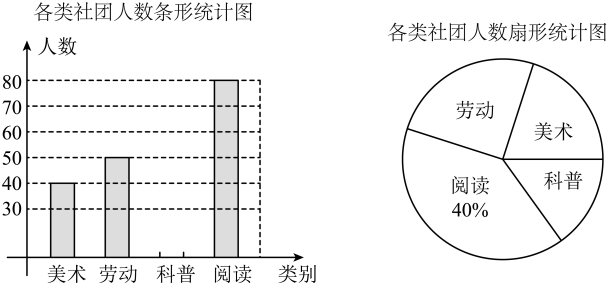 (1)、求本次调查的学生人数,并补全条形统计图;(2)、若全校共有学生3600人,求愿意参加劳动类社团的学生人数;(3)、甲、乙两名同学决定在阅读、美术、劳动社团中选择参加一种社团,请用树状图或列表法表示出所有等可能结果,并求出恰好选中同一社团的概率.23. 如图,一次函数经过点 , , 与反比例函数的图象交于点 , 两点.
(1)、求本次调查的学生人数,并补全条形统计图;(2)、若全校共有学生3600人,求愿意参加劳动类社团的学生人数;(3)、甲、乙两名同学决定在阅读、美术、劳动社团中选择参加一种社团,请用树状图或列表法表示出所有等可能结果,并求出恰好选中同一社团的概率.23. 如图,一次函数经过点 , , 与反比例函数的图象交于点 , 两点. (1)、求反比例函数和一次函数的解析式;(2)、求的面积.24. 某水果店以进价为每千克元购进草莓,销售中发现,销售单价定为元时,日销售量为千克;当销售单价每上涨元,日销售量就减少千克,设销售单价为元,每天的销售量为千克,每天获利为元.(1)、求与之间的函数表达式;(2)、求与之间的函数表达式,并求该草莓售价定为每千克多少元时,每天的销售利润最大?最大利润是多少元?(3)、如果商家规定这种草莓每天的销售量不低于千克,求每天销售利润的最大值是多少元?25. 在等腰直角三角形中, , , 分别为 , 的中点,为的中点,连接 .
(1)、求反比例函数和一次函数的解析式;(2)、求的面积.24. 某水果店以进价为每千克元购进草莓,销售中发现,销售单价定为元时,日销售量为千克;当销售单价每上涨元,日销售量就减少千克,设销售单价为元,每天的销售量为千克,每天获利为元.(1)、求与之间的函数表达式;(2)、求与之间的函数表达式,并求该草莓售价定为每千克多少元时,每天的销售利润最大?最大利润是多少元?(3)、如果商家规定这种草莓每天的销售量不低于千克,求每天销售利润的最大值是多少元?25. 在等腰直角三角形中, , , 分别为 , 的中点,为的中点,连接 . (1)、如图 , 过作于 , 交于 , 直接写出线段与的数量关系;(2)、将绕点顺时针旋转到如图所示位置,过作于 , 过作的平行线与直线交于点 , 得到线段 , .
(1)、如图 , 过作于 , 交于 , 直接写出线段与的数量关系;(2)、将绕点顺时针旋转到如图所示位置,过作于 , 过作的平行线与直线交于点 , 得到线段 , .中的结论是否成立?请说明理由;
从图的位置开始将绕点顺时针旋转,当 , , 共线时,直接写出的长度.
26. 如图 , 已知二次函数的图象与轴交于点、 , 与轴交于点 , 且 . (1)、求二次函数的解析式;(2)、如图 , 过点作轴交二次函数图象于点 , 是二次函数图象上异于点的一个动点,连接、 , 若 , 求点的坐标;(3)、如图 , 若点是二次函数图象上位于下方的一个动点,连接交于点设点的横坐标为 , 试用含的代数式表示的值,并求的最大值.
(1)、求二次函数的解析式;(2)、如图 , 过点作轴交二次函数图象于点 , 是二次函数图象上异于点的一个动点,连接、 , 若 , 求点的坐标;(3)、如图 , 若点是二次函数图象上位于下方的一个动点,连接交于点设点的横坐标为 , 试用含的代数式表示的值,并求的最大值.
-