贵州省铜仁市石阡县2023-2024学年九年级下学期3月月考数学试题
试卷更新日期:2024-04-25 类型:月考试卷
一、选择题(本大题共12小题,每小题3分,共36分.在每小题所给的四个选项中,有且只有一项是符合题目要求的)
-
1. 若抛物线的开口向下,则a的值可以是( )A、1 B、 C、2 D、52. 如图,是的圆周角, , 则的度数为( ).
 A、 B、 C、 D、3. 某几何体的三视图如图所示,该几何体是( )
A、 B、 C、 D、3. 某几何体的三视图如图所示,该几何体是( ) A、长方体 B、圆锥 C、直三棱柱 D、圆柱4. 在一个不透明的盒子中,装有绿球和白球共60个,这些球除颜色外其他完全相同.从盒子中随机摸出一个球,记下颜色后放回摇匀,通过多次摸球试验发现,摸到绿球的频率稳定在左右,则盒子中白球的个数可能是( )A、48个 B、42个 C、32个 D、18个5. 一个立体图形的侧面展开图如图所示,则该立体图形的底面形状是( )
A、长方体 B、圆锥 C、直三棱柱 D、圆柱4. 在一个不透明的盒子中,装有绿球和白球共60个,这些球除颜色外其他完全相同.从盒子中随机摸出一个球,记下颜色后放回摇匀,通过多次摸球试验发现,摸到绿球的频率稳定在左右,则盒子中白球的个数可能是( )A、48个 B、42个 C、32个 D、18个5. 一个立体图形的侧面展开图如图所示,则该立体图形的底面形状是( ) A、
A、 B、
B、 C、
C、 D、
D、 6. 质检部门从4000件电子元件中随机抽取100件进行检测,其中有2件是次品,据此估计这批电子元件中次品数量大约为( )A、2件 B、8件 C、20件 D、80件7. 如图,以点O为位似中心,把的各边长放大为原来的2倍得到 , 下列说法中,错误的是( )
6. 质检部门从4000件电子元件中随机抽取100件进行检测,其中有2件是次品,据此估计这批电子元件中次品数量大约为( )A、2件 B、8件 C、20件 D、80件7. 如图,以点O为位似中心,把的各边长放大为原来的2倍得到 , 下列说法中,错误的是( ) A、 B、 C、 D、A,O,三点在同一条直线上8. 如图,正六边形的边长为6,以顶点A为圆心,的长为半径画圆,则图中阴影部分的面积为( )
A、 B、 C、 D、A,O,三点在同一条直线上8. 如图,正六边形的边长为6,以顶点A为圆心,的长为半径画圆,则图中阴影部分的面积为( ) A、 B、 C、 D、9. 下列成语所描述的事件属于不可能事件的是( )A、海底捞月 B、水涨船高 C、旭日东升 D、水滴石穿10. 若二次函数的图象经过 , , 三点,则关于 , , 的大小关系正确的是( )A、 B、 C、 D、11. 如图是一个隧道的横截面,若它的形状是以为圆心的圆的一部分,路面米,高米,则此圆的半径的长度为( )
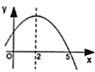
A、 B、 C、 D、9. 下列成语所描述的事件属于不可能事件的是( )A、海底捞月 B、水涨船高 C、旭日东升 D、水滴石穿10. 若二次函数的图象经过 , , 三点,则关于 , , 的大小关系正确的是( )A、 B、 C、 D、11. 如图是一个隧道的横截面,若它的形状是以为圆心的圆的一部分,路面米,高米,则此圆的半径的长度为( ) A、米 B、米 C、米 D、米12. 已知抛物线的对称轴为直线 , 与x轴的一个交点为 , 其部分图象如图所示,下列结论:①抛物线过原点;②;③;④ . 其中正确的有( )
A、米 B、米 C、米 D、米12. 已知抛物线的对称轴为直线 , 与x轴的一个交点为 , 其部分图象如图所示,下列结论:①抛物线过原点;②;③;④ . 其中正确的有( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题(本大题共4小题,每小题4分,共16分)
-
13. 阳光下广告牌的影子属于投影(填“中心”或“平行”).14. 若关于的一元二次方程有实数根,则的最大值为 .15. 如图,是二次函数 的部分图象,由图象可知不等式 的解集是.
 16. 如图,直线 , 相交于点O, , 半径为的的圆心在直线上,且位于点O左侧处.若以的速度由A向B的方向移动,则后,与直线相切.
16. 如图,直线 , 相交于点O, , 半径为的的圆心在直线上,且位于点O左侧处.若以的速度由A向B的方向移动,则后,与直线相切.
三、解答题(本大题共9小题,共98分.解答时应写出必要的文字说明、证明过程或演算步骤)
-
17. 在平面直角坐标系中,已知抛物线 .(1)、它的顶点坐标是 , 当x的取值范围为时,y随x的增大而减小;(2)、将抛物线先向左平移2个单位,再向下平移3个单位,求所得新抛物线与x轴的交点坐标.18. 如图,路灯下一墙墩(用线段表示)的影子是 , 小明(用线段表示)的影子是 , 在M处有一棵大树,它在这个路灯下的影子是 .
 (1)、在图中画出路灯的位置并用点P表示;(2)、在图中画出表示大树的线段 .19. 如图是一款近似圆锥形帐篷,其侧面展开后是一个半径为、圆心角为的扇形,制作这顶帐篷(侧面与底面)需要多少平方米的材料?(结果保留)
(1)、在图中画出路灯的位置并用点P表示;(2)、在图中画出表示大树的线段 .19. 如图是一款近似圆锥形帐篷,其侧面展开后是一个半径为、圆心角为的扇形,制作这顶帐篷(侧面与底面)需要多少平方米的材料?(结果保留) 20. 如图所示,中, , 以为直径作 , 交边于点D,交的延长线于点E,连接 .
20. 如图所示,中, , 以为直径作 , 交边于点D,交的延长线于点E,连接 . (1)、求证:;(2)、若 , 求的长.21. 如图,一次函数的图象与反比例函数的图象交于点A与点 .
(1)、求证:;(2)、若 , 求的长.21. 如图,一次函数的图象与反比例函数的图象交于点A与点 . (1)、求反比例函数的表达式;(2)、连接 , , 求的面积.22. 暑假期间,小明和小张计划外出游玩,准备通过抽卡片的方式每人从下面四个景点A:石阡佛顶山;B:莲华古风景区;C:楼上古寨;D:贵州三昧禅院中各随机选择一个.(1)、小明选择去石阡佛顶山的概率为;(2)、请用画树状图或列表的方法,求小明和小张去同一景区的概率.23. 除夕夜小李和亮亮相约去看烟花,并测量烟花的燃放高度.如图,小李从点B处出发,沿坡度为的山坡走了到达坡顶点A处,亮亮则到达离点A水平距离为的点C处观看,此时烟花在与B,C同一水平线上的点D处点燃,一朵朵灿烂的烟花在点D的正上方点E处绽放,小李在坡顶A处看烟花绽放处E的仰角为 , 亮亮在C处测得点E的仰角为 . (点A,B,C,D,E在同一平面内;参考数据: , )
(1)、求反比例函数的表达式;(2)、连接 , , 求的面积.22. 暑假期间,小明和小张计划外出游玩,准备通过抽卡片的方式每人从下面四个景点A:石阡佛顶山;B:莲华古风景区;C:楼上古寨;D:贵州三昧禅院中各随机选择一个.(1)、小明选择去石阡佛顶山的概率为;(2)、请用画树状图或列表的方法,求小明和小张去同一景区的概率.23. 除夕夜小李和亮亮相约去看烟花,并测量烟花的燃放高度.如图,小李从点B处出发,沿坡度为的山坡走了到达坡顶点A处,亮亮则到达离点A水平距离为的点C处观看,此时烟花在与B,C同一水平线上的点D处点燃,一朵朵灿烂的烟花在点D的正上方点E处绽放,小李在坡顶A处看烟花绽放处E的仰角为 , 亮亮在C处测得点E的仰角为 . (点A,B,C,D,E在同一平面内;参考数据: , ) (1)、小李从斜坡B处走到A处,高度上升了多少米?(2)、烟花燃放结束后,小李和亮亮来到烟花燃放地帮忙清理现场的垃圾,他们清理时发现说明书上写着烟花的燃放高度为 , 请你帮他们计算一下,说明书上写的烟花燃放高度与实际燃放高度(图中)是否相符?24. 如图,是的直径,垂直于弦于点E,且交于点D,F是延长线上一点,若 .
(1)、小李从斜坡B处走到A处,高度上升了多少米?(2)、烟花燃放结束后,小李和亮亮来到烟花燃放地帮忙清理现场的垃圾,他们清理时发现说明书上写着烟花的燃放高度为 , 请你帮他们计算一下,说明书上写的烟花燃放高度与实际燃放高度(图中)是否相符?24. 如图,是的直径,垂直于弦于点E,且交于点D,F是延长线上一点,若 . (1)、求证,是的一条切线;(2)、若 , , 求的长.25. 某俱乐部购进一台如图1的篮球发球机,用于球员篮球训练.该发球机可以以不同力度发射出篮球,篮球运行的路线都是抛物线.出球口离地面高1米,以出球口为原点,平行于地面的直线为x轴,垂直于地面的直线为y轴,建立平面直角坐标系.力度变化时,抛物线的顶点在直线上移动,从而产生一组不同的抛物线(如图2).
(1)、求证,是的一条切线;(2)、若 , , 求的长.25. 某俱乐部购进一台如图1的篮球发球机,用于球员篮球训练.该发球机可以以不同力度发射出篮球,篮球运行的路线都是抛物线.出球口离地面高1米,以出球口为原点,平行于地面的直线为x轴,垂直于地面的直线为y轴,建立平面直角坐标系.力度变化时,抛物线的顶点在直线上移动,从而产生一组不同的抛物线(如图2). (1)、若 .
(1)、若 .①发球机发射出的篮球运行到距发球机水平距离为6m时,离地面的高度为1m.请直接写出该球在运行过程中离地面的最大高度;
②若发球机发射出的篮球在运行过程中离地面的最大高度为3m,求该球运行路线的解析式,及此球落地点离发球机的水平距离;
(2)、球员小刚训练时发现:当篮球运行到离地面高度为1m至2.2m之间(包含端点)是最佳接球区间,若 , 直接写出当a满足什么条件时,距发球机水平距离12m的小刚在前后不挪动位置的前提下,能在最佳区间接到球.