浙江省宁波市镇海区蛟川书院2020-2021学年七年级下册期中数学试卷

试卷更新日期：2024-04-24 类型：期中考试

进入出卷网下载

一、选择题（本题共10小题，每小题3分，共30分。在每小题给出的四个选项中，只有一项是符合题目要求的）

1. 若分式 $\frac{6 x}{x - 5}$ 有意义，则x满足的条件是（　　）

A、x＝5 B、x≠5 C、x＝0 D、x≠0

查看试题解析
2. 在下列图形中，∠1与∠2是同位角的是（）

A、 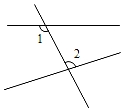B、 C、 D、

查看试题解析
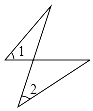3. 列方程组解古算题：“今有共买物，人出八，盈三；人出七，不足四，问人数、物价各几何？”题目大意是：几个人共同购买一件物品，每人出8钱，余3钱；每人出7钱，缺4钱．设参与共同购物的有x个人，物品价值y钱，可列方程组为（　　）

A、 $\{\begin{array}{l} 8 x - 3 = y \\ 7 x + 4 = y \end{array}$ B、 $\{\begin{array}{l} 8 x + 3 = y \\ 7 x - 4 = y \end{array}$ C、 $\{\begin{array}{l} 8 x - 3 = y \\ 7 x - 4 = y \end{array}$ D、 $\{\begin{array}{l} 8 x + 3 = y \\ 7 x + 4 = y \end{array}$

查看试题解析
4. 如图，将三角形ABE向右平移1cm得到三角形DCF ，如果三角形ABE的周长是10cm ，那么四边形ABFD的周长是（　　）

A、12cm B、16cm C、18cm D、20cm

查看试题解析
5. 若（a^mbⁿ）³=a⁹b¹⁵ ，则m、n的值分别为（）

A、9；5 B、3；5 C、5；3 D、6；12

查看试题解析
6. 若关于x ， y的方程组 $\{\begin{array}{l} x - y = 2 \\ m x + y = 6 \end{array}$ 有非负整数解，则正整数m为（　　）

A、0，1 B、1，3，7 C、0，1，3 D、1，3

查看试题解析
7. 已知d＝x⁴﹣2x³+x²﹣8x+11，则当x²﹣2x﹣3＝0时，d的值为（　　）

A、25 B、24 C、23 D、22

查看试题解析
8. 已知a ， b ， c是正整数，a＞b ，且a²﹣ab﹣ac+bc＝13，则a﹣c等于（　　）

A、﹣1 B、﹣1或﹣13 C、1 D、1或13

查看试题解析
9. 已知5x²+2xy﹣3y²＝0（x≠0，y≠0），则 $\frac{2}{y} - \frac{y}{x} - \frac{2 x + y^{2}}{x y}$ 的值为（　　）

A、2或 $- \frac{10}{3}$ B、﹣1或 $\frac{5}{3}$ C、 $- \frac{10}{3}$ D、 $\frac{5}{3}$

查看试题解析
10. 在矩形ABCD内，将一张边长为a和两张边长为b（a＞b）的正方形纸片按图1，图2两种方式放置，矩形中未被这三张正方形纸片覆盖的部分用阴影表示，设图2中阴影部分的周长与图1中阴影部分的周长的差为l ，若要知道l的值，只要测量图中哪条线段的长（　　）

A、AB B、AD C、a D、b

查看试题解析

二、填空题（本题共8小题，每小题3分，共24分，请把答案填写在相应的空格内）

11. 因式分解2x²﹣4x+2= ．

查看试题解析
12. 如图把三角板的直角顶点放在直线 $b$ 上，若 $∠ 1 = 38 °$ ，则当 $∠ 2 =$ 度时， $a ∥ b$ ．

查看试题解析
13. 已知 $a b = 3$ ， $a + b = 4$ ，则代数式 $a^{3} b + a b^{3}$ 的值为．

查看试题解析
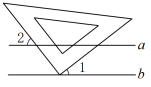14. 已知在（x²+ax+b）（2x²﹣3x﹣1）的积中，含x²项的系数为10，不含x项，则a+b的值为．

查看试题解析
15. 计算： $2 (1 + \frac{1}{3}) (1 + \frac{1}{3^{2}}) (1 + \frac{1}{3^{4}}) (1 + \frac{1}{3^{8}}) + \frac{1}{3^{15}} =$ ．

查看试题解析
16. 若关于x的方程 $\frac{a x}{x + 1} = \frac{3}{x + 1} + 2$ 无解，则a的值是．

查看试题解析
17. 若关于x、y的方程组 $\{\begin{array}{l} a_{1} x + b_{1} y = c_{1} \\ a_{2} x + b_{2} y = c_{2} \end{array}$ 的解是 $\{\begin{array}{l} x = 5 \\ y = 4 \end{array}$ ，则方程组 $\{\begin{array}{l} a_{1} x + b_{1} y = 5 c_{1} - 4 a_{1} \\ a_{2} x + b_{2} y = 5 c_{2} - 4 a_{2} \end{array}$ 的解为．

查看试题解析
18. 已知 $\frac{1}{b} - \frac{1}{a} = \frac{8 - c}{a b}$ ， ab+bc+2b+c²+25＝0，则 $\frac{b}{a}$ 的值为．

查看试题解析

三、解答题（本题共6小题，共46分）

19.

(1)、计算：（x﹣1）（x+1）﹣（x+1）² ．

(2)、解方程： $\frac{2 x}{3 x - 3} = \frac{x}{x - 1} - 1$ ．

查看试题解析
20. 先化简：（ $\frac{a + 7}{a - 1} - \frac{2}{a + 1}$ ） $\div \frac{a^{2} + 3 a}{a^{2} - 1}$ ，再从﹣3、﹣2、﹣1、0、1中选一个合适的数作为a的值代入求值．

查看试题解析
21. 甲、乙两人共同解方程组 $\{\begin{array}{l} a x - b y = - \frac{11}{2} ① \\ a x + b y = 5 ② \end{array}$ ，由于甲看错了方程①中的a ，得到方程组的解为 $\{\begin{array}{l} x = 2 \\ y = 3 \end{array}$ ，乙看错了方程②中的b ，得到方程组的解为 $\{\begin{array}{l} x = 3 \\ y = 2 \end{array}$ ，试求出a ， b的正确值，并计算a²⁰²¹•b²⁰²⁰的值．

查看试题解析
22. 某工厂计划在规定时间内生产27000个零件．若每天比原计划多生产60个零件，则在规定时间内可以多生产600个零件．

(1)、求原计划每天生产的零件个数和规定的天数；

(2)、为了提前完成生产任务，工厂在安排原有工人按原计划正常生产的同时，引进5组机器人生产流水线共同参与零件生产，已知每组机器人生产流水线每天生产零件的个数比10个工人原计划每天生产的零件总数还多20%，按此测算，恰好提前一天完成27000个零件的生产任务，求原计划安排的工人人数．

查看试题解析
23. 若一个两位正整数m的个位数为4，则称m为“好数“．

(1)、求证：对任意“好数”m ， m²﹣16一定为20的倍数；

(2)、若m＝p²﹣q² ，且p ， q为正整数，则称数对（p ， q）为“友好数对”，规定：H（m） $= \frac{q}{p}$ ，例如24＝5²﹣1² ，称数对（5，1）为“友好数对”，则 $H (24) = \frac{1}{5}$ ，求小于70的“好数”中，所有“友好数对”的H（m）的最大值．

查看试题解析
24. 已知AB∥CD ，点M、N分别为AB、CD上的点，在AB、CD之间存在一点P满足MP⊥PN ．

(1)、如图1，若∠AMP＝α，求∠PNC的度数（用含α的代数式表达）．

(2)、如图2，过点P作PH⊥AB于点H ，点E、F在AB上，连接PE、PF、NF ，若PE平分∠HPM ， PF平分∠HPN ，求∠EPF与∠MPN的数量关系．

(3)、在（2）的条件下，若∠PNF+∠CNF＝180°，∠PFN＝2∠HPE ，求∠EPN的度数．

查看试题解析