广东省河源市江东新区2023-2024学年八年级上学期期末数学试题
试卷更新日期:2024-04-23 类型:期末考试
一、单项选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.
-
1. 下列计算,正确的是( )A、 B、 C、 D、2. 在中,斜边 , 则的值为( )A、15 B、25 C、50 D、无法计算3. 下列命题的逆命题是真命题的是( )A、两直线平行,内错角相等 B、如果 , 那么 C、钝角三角形中有两个锐角 D、对顶角相等4. 点和都在直线上,且 , 则与的关系是( )A、 B、 C、 D、5. “歼20是我国自主研制的第五代战斗机,属于单座双发隐形战斗机,具备高隐身性、高态势感知、高机动性的特点.如图,小静将一张“歼”一飞冲天的图片放入网格中,若图片上点B的坐标为 , 点C的坐标为 , 则点A的坐标为( )
 A、 B、 C、 D、6. 如图,下列条件中不能判定的是( )
A、 B、 C、 D、6. 如图,下列条件中不能判定的是( ) A、 B、 C、 D、7. 点与点关于直线对称,则点的坐标为( )
A、 B、 C、 D、7. 点与点关于直线对称,则点的坐标为( ) A、 B、 C、 D、8. 甲乙两班的学生人数相等,参加了同一次数学测试,两班的平均分都是89分,方差分别为 , , 那么成绩比较整齐的班级是( )A、甲班 B、乙班 C、两班一样整齐 D、无法确定9. 如图,某学校举办元旦联欢会,准备在舞台侧长 , 高的台阶上铺设红地毯,已知台阶的宽为 , 则共需购买红地毯( )
A、 B、 C、 D、8. 甲乙两班的学生人数相等,参加了同一次数学测试,两班的平均分都是89分,方差分别为 , , 那么成绩比较整齐的班级是( )A、甲班 B、乙班 C、两班一样整齐 D、无法确定9. 如图,某学校举办元旦联欢会,准备在舞台侧长 , 高的台阶上铺设红地毯,已知台阶的宽为 , 则共需购买红地毯( ) A、 B、 C、 D、10. 甲、乙两车从A地驶向B地,并以各自的速度匀速行驶,甲车比乙车早行驶 ,并且甲车途中休息了 ,如图是甲、乙两车行驶的距离 与时间 的函数图象,有以下结论:
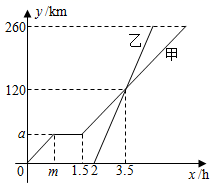
A、 B、 C、 D、10. 甲、乙两车从A地驶向B地,并以各自的速度匀速行驶,甲车比乙车早行驶 ,并且甲车途中休息了 ,如图是甲、乙两车行驶的距离 与时间 的函数图象,有以下结论:① ;② ;③甲车从A地到B地共用了7小时;④当两车相距 时,乙车用时为 .其中正确结论的个数是( ).
 A、4 B、3 C、2 D、1
A、4 B、3 C、2 D、1二、填空题(本大题6小题,每小题3分,共18分)
-
11. 写出一个解为 的二元一次方程组 .12. 如图,在原点为O的数轴上,作一个两直角边长分别是1和2,斜边为的直角三角形,点A在点O左边的数轴上,且 , 则点A表示的实数是 .
 13. 直线平行于直线 , 且过点 , 则其解析式为 .14. 如图,在一棵树的10米高的处有两只猴子为抢吃池塘边水果,一只猴子爬下树跑到处(离树20米)的池塘边,另一只爬到树顶后直接跃到处,距离以直线计算,若两只猴子所经过的距离相等,则这棵树高米.
13. 直线平行于直线 , 且过点 , 则其解析式为 .14. 如图,在一棵树的10米高的处有两只猴子为抢吃池塘边水果,一只猴子爬下树跑到处(离树20米)的池塘边,另一只爬到树顶后直接跃到处,距离以直线计算,若两只猴子所经过的距离相等,则这棵树高米. 15. 如图,直线与直线相交于点 , 则方程组的解为 .
15. 如图,直线与直线相交于点 , 则方程组的解为 . 16. 如图,在中, , 和的平分线交于点 , 得;和的平分线交于点 , 得;…;和的平分线交于点 , 则°.
16. 如图,在中, , 和的平分线交于点 , 得;和的平分线交于点 , 得;…;和的平分线交于点 , 则°.
三、解答题(本大题共9小题,满分72分,解答应写出文字说明、证明过程或演算步骤)
-
17. 计算: .18. 计算: .19. 解方程组: .20. 计算: .21. 已知 , D为上一点, .
 (1)、尺规作图:在边上求作一点F , 使得;(保留作图痕迹,不写作法)(2)、求的度数.22. 已知:如图 , , , .
(1)、尺规作图:在边上求作一点F , 使得;(保留作图痕迹,不写作法)(2)、求的度数.22. 已知:如图 , , , . (1)、与平行吗?为什么?(2)、求:的度数.23. 西川实验学校为调查本校学生周末平均每天做作业所用时间的情况,随机调查了50名同学,如图是根据调查所得数据绘制的统计图的一部分.请根据以上信息.
(1)、与平行吗?为什么?(2)、求:的度数.23. 西川实验学校为调查本校学生周末平均每天做作业所用时间的情况,随机调查了50名同学,如图是根据调查所得数据绘制的统计图的一部分.请根据以上信息.解答下列问题
 (1)、请你补全条形统计图:(2)、在这次调查的数据中,做作业所用时间的众数是小时,中位数是小时,平均数是小时;(3)、若该校共有1500名学生,根据以上调查结果估计该校全体学生每天做作业时间在3小时内(含3小时)同学共有多少人?24. 为迎接“国家卫生城市”复检,某市环卫局准备购买A , B两种型号的垃圾箱,通过市场调研得知:购买3个A型垃圾箱和2个B型垃圾箱共需540元;购买2个A型垃圾箱比购买3个B型垃圾箱少用160元.(1)、求每个A型垃圾箱和B型垃圾箱各多少元.(2)、该市现需要购买A , B两种型号的垃圾箱共30个,其中购买A型垃圾箱不超过16个.
(1)、请你补全条形统计图:(2)、在这次调查的数据中,做作业所用时间的众数是小时,中位数是小时,平均数是小时;(3)、若该校共有1500名学生,根据以上调查结果估计该校全体学生每天做作业时间在3小时内(含3小时)同学共有多少人?24. 为迎接“国家卫生城市”复检,某市环卫局准备购买A , B两种型号的垃圾箱,通过市场调研得知:购买3个A型垃圾箱和2个B型垃圾箱共需540元;购买2个A型垃圾箱比购买3个B型垃圾箱少用160元.(1)、求每个A型垃圾箱和B型垃圾箱各多少元.(2)、该市现需要购买A , B两种型号的垃圾箱共30个,其中购买A型垃圾箱不超过16个.①求购买垃圾箱的总花费w(元)与购买A型垃圾箱的个数x之间的函数关系式;
②当购买A型垃圾箱多少个时总费用最少,最少费用是多少?
25. 如图,正比例函数的图像与一次函数的图像交于点 , 一次函数图象经过点 , 与y轴的交点为D , 与x轴的交点为C . (1)、求一次函数表达式;(2)、求D点的坐标;(3)、求的面积.
(1)、求一次函数表达式;(2)、求D点的坐标;(3)、求的面积.