广西南宁天桃教育集团2023-2024学年八年级下学期数学3月月考试卷

试卷更新日期：2024-04-23 类型：月考试卷

进入出卷网下载

一、选择题（本大题共12题，每小题3分，共36分）

1. “剪纸舞东方，春意彩添堂”，剪纸是我国最古老的民间艺术之一，下列剪纸作品中，是轴对称图形的为（）

A、 B、 C、 D、

查看试题解析
2. 下列式子中，是二次根式的是( )

A、 $π$ B、 $\frac{1}{3}$ C、-2 D、 $\sqrt{3}$

查看试题解析
3. 已知一组数据：2，3，2，5，2，2，4，这组数据的众数是（）

A、2 B、3 C、4 D、5

查看试题解析
4. 如图，在 $△ A B C$ 中，D是 $B C$ 延长线上一点， $∠ A = 70 °, ∠ B = 40 °$ ，则 $∠ A C D$ 的度数为（）

A、100° B、110° C、120° D、130°

查看试题解析
5. 以下列数作为三角形的边长，其中能构成直角三角形的是（）

A、3，4，5 B、1，2，3 C、6，9，12 D、5，8，10

查看试题解析
6. 如图， $R t △ A B C ≌ R t △ D B E$ ，若 $∠ A = 30 °$ ，则 $∠ E$ 的度数为（）

A、 $60 °$ B、 $45 °$ C、 $35 °$ D、 $30 °$

查看试题解析
7. 如图， $O C$ 平分 $∠ A O B$ ，在 $O C$ 上取一点P ，过P作 $P Q ⊥ O B$ ，若 $P Q = 7 c m$ ，则点P到OA的距离为( )

A、 $4 c m$ B、 $5 c m$ C、 $6 c m$ D、 $7 c m$

查看试题解析
8. 下列计算，正确的是（）

A、 $a^{2} \cdot a^{3} = a^{6}$ B、 $a^{2} + a^{3} = a^{5}$ C、 ${(- a^{2})}^{3} = - a^{6}$ D、 $a^{6} \div {(- a)}^{3} = - a^{2}$

查看试题解析
9. 若分式方程 $\frac{a + 1}{x} = 1$ 的解是 $x = 2$ ．则 $a =$ （）

A、 $- 1$ B、3 C、 $- 3$ D、1

查看试题解析
10. 若将 $\frac{5 x}{x + y}$ 中的 $x$ 与 $y$ 都扩大为原来的10倍，则这个代数式的值（）

A、扩大为原来的10倍 B、扩大为原来的50倍 C、缩小为原来的10倍 D、不变

查看试题解析
11. 如图，在 $△ A B C$ 中， $∠ B A C = 120 °$ ，点D是BC上一点，BD的垂直平分线交AB于点E，将 $△ A C D$ 沿AD折叠，点C恰好与点E重合，则 $∠ B$ 等于（）

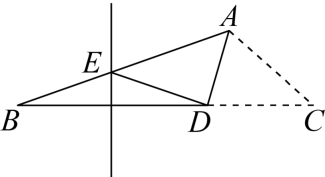A、19° B、20° C、24° D、25°

查看试题解析
12. 有两个正方形A、B ，将A、B并列放置后构造新的图形，分别得到长方形图甲与正方形图乙．若图甲、图乙中阴影的面积分别为12与30，则正方形B的面积为（）

A、 $3$ B、 $4$ C、 $5$ D、 $6$

查看试题解析

二、填空题（本大题共6题，每小题2分，共12分）

13. 计算： $3^{- 1} =$

查看试题解析
14. 若分式 $\frac{x - 1}{x}$ 的值为0，则 $x$ 的值为.

查看试题解析
15. 一个多边形的内角和是1080°，那么这个多边形的边数 $n =$ ．

查看试题解析
16. 如图，一棵大树（树干与地面垂直）在一次强台风中于离地面5米的B处折断倒下，倒下后的树顶C与树根A的距离为12米，则这棵大树在折断前的高度为米．

查看试题解析
17. 已知 $a - b = 5$ ， $a b = 2$ ，则 $a b^{2} - a^{2} b =$ ．

查看试题解析
18. 如图，在四边形 $A B C D$ 中， $∠ C = α °$ ， $∠ B = ∠ D = 90 °$ ， E ， F分别是 $B C$ ， $D C$ 上的点，当 $△ A E F$ 的周长最小时， $∠ E A F$ 的度数为．

查看试题解析

三、解答题（本大题共8小题，共72分）

19. 计算： $2 \times (3 + \sqrt{5}) - 2 \sqrt{5}$ ．

查看试题解析
20. 先化简： $(\frac{3 a}{a - 2} - \frac{a}{a - 2}) \div \frac{2 a}{a^{2} - 4}$ ，再从-2，0，1，2中选择一个合适的数代入求值．

查看试题解析
21. 如图， $∠ E A C$ 是 $△ A B C$ 的外角， $A B = A C$ ．

(1)、请你用尺规作图的方法作 $∠ E A C$ 的角平分线 $A D$ ；（不写作法，保留作图痕迹）

(2)、判断 $A D$ 与 $B C$ 的位置关系，并说明理由．

查看试题解析
22. 如图，在△ABC中， $D$ 是 $B C$ 的中点， $D E ⊥ A B$ ， $D F ⊥ A C$ ，垂足分别是 $E$ 、 $F$ ，且 $B E = C F$ ．

(1)、求证： $∠ B = ∠ C$ ．

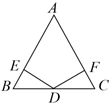(2)、连接AD，求证：AD⊥BC．

查看试题解析
23. 为让学生了解广西的历史、地理等方面的知识，增强文化教育，某校组织学生进行“壮美家乡知多少”知识竞赛，满分 $10$ 分，学生得分均为整数．在初赛中，甲、乙两组 $($ 每组 $10$ 人 $)$ 学生成绩如下 $($ 单位：分 $)$ ：
甲组： $3$ ， $6$ ， $6$ ， $6$ ， $6$ ， $6$ ， $7$ ， $9$ ， $9$ ， $10 .$
乙组： $5$ ， $6$ ， $6$ ， $6$ ， $7$ ， $7$ ， $7$ ， $7$ ， $8$ ， $9 .$
组别
平均数
中位数
众数
方差
甲组
$6.8$
$a$
$6$
3.76
乙组
$b$
$7$
$c$
1.16

(1)、以上成绩统计分析表中 $a =$ ， $b =$ ， $c =$ ；

(2)、小明同学说：“这次竞赛我得了7分，在我们小组中属中游略偏上！”观察上面表格判断，小明可能是组的学生；

(3)、从平均数和方差看，若从甲、乙两组学生中选择一个组参加决赛，应选哪个组？并说明理由．

查看试题解析
24. 某数学兴趣小组开展了“笔记本电脑张角大小与顶部边缘离桌面高度之间的关系”的实践探究活动．如图，当张角为 $∠ B A F$ 时，顶部边缘点 $B$ 离桌面的高度 $B C$ 为 $7 c m$ ，此时底部边缘点 $A$ 与点 $C$ 之间的距离 $A C$ 为 $24 c m$ ．

(1)、求 $A B$ 的长度．

(2)、若小组成员调整张角的大小继续探究，发现当张角为 $∠ D A F$ 时（点D为点B的对应点），顶部边缘点D离桌面的高度为 $D E$ ，此时底部边缘点A与点E之间的距离 $A E$ 为 $15 c m$ ，求此时电脑顶部边缘上升的高度．

查看试题解析
25. 小刚到离家 $1200$ 米的电影院看电影，到电影院时发现钱包丢在家里，此时距电影放映还有 $25$ 分钟，于是他立即步行（匀速）回家，在家拿钱包用了 $2$ 分钟，然后骑自行车（匀速）返回电影院，已知小刚骑自行车的速度是步行速度的 $2.5$ 倍，小刚骑自行车到电影院比他从电影院步行到家少用了 $9$ 分钟．

(1)、小刚步行的速度是每分钟多少米？

(2)、小刚能否在电影放映前赶到电影院？

查看试题解析
26. 已知，在等边三角形 $A B C$ 中，点 $E$ 在 $A B$ 上，点 $D$ 在 $C B$ 的延长线上，且 $E D = E C$ ．

(1)、【特殊情况，探索结论】如图1，当点 $E$ 为 $A B$ 的中点时，确定线段 $A E$ 与 $D B$ 的大小关系，请你直接写出结论： $A E$ $D B$ 填“ $>$ ”，“ $<$ ”或“ $=$ ” $)$ ．

(2)、【特例启发，解答题目】如图2，当点 $E$ 为 $A B$ 边上任意一点时，请判断线段 $A E$ 与 $D B$ 的大小关系，并说明理由．

(3)、【拓展结论，设计新题】在等边三角形 $A B C$ 中，点 $E$ 在直线 $A B$ 上，点 $D$ 在线段 $C B$ 的延长线上，且 $E D = E C$ ，若 $△ A B C$ 的边长为3， $A E = 6$ ，求线段 $C D$ 的长．

查看试题解析

组别	平均数	中位数	众数	方差
甲组	$6.8$	$a$	$6$	3.76
乙组	$b$	$7$	$c$	1.16