2024年人教A版高二下学期数学期中模拟试卷一(新题型)
试卷更新日期:2024-04-22 类型:期中考试
一、选择题(每题4分,共40分)
-
1. 已知集合 , , 则( )A、 B、 C、 D、2. 设数列的公比为 , 则“且”是“是递减数列”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件3. 已知向量满足 , 则( )A、-2 B、2 C、-4 D、44. 已知抛物线的焦点为F , 为抛物线上一动点,点 , 则周长的最小值为( )A、13 B、14 C、15 D、165. 我国著名数学家华罗庚先生曾说:“数缺形时少直观,形缺数时难入微,数形结合百般好,隔裂分家万事休.”在数学的学习和研究中,常用函数的图象来研究函数的性质,也常用函数的解析式来琢磨函数的图象的特征,如函数的图象大致是( )A、
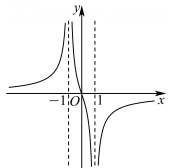 B、
B、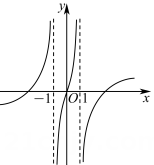 C、
C、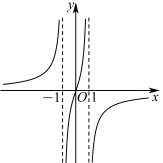 D、
D、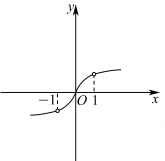 6. 已知函数 , , 的零点分别为a,b,c,下列各式正确的是( )A、 B、 C、 D、7. 设圆和不过第三象限的直线 , 若圆上恰有三点到直线的距离为3,则实数( )A、2 B、4 C、26 D、418. 已知函数 , 若总存在两条不同的直线与函数 , 图象均相切,则实数的取值范围是( )A、 B、 C、 D、
6. 已知函数 , , 的零点分别为a,b,c,下列各式正确的是( )A、 B、 C、 D、7. 设圆和不过第三象限的直线 , 若圆上恰有三点到直线的距离为3,则实数( )A、2 B、4 C、26 D、418. 已知函数 , 若总存在两条不同的直线与函数 , 图象均相切,则实数的取值范围是( )A、 B、 C、 D、二、多项选择题(每题6分,共18分)
-
9. 已知的展开式的各项系数之和为1024,则展开式中( )A、奇数项的二项式系数和为256 B、第6项的系数最大 C、存在常数项 D、有理项共有6项10. “阿基米德多面体”又称“半正多面体”,与正多面体类似,它们也都是凸多面体,每个面都是正多边形,并且所有棱长也都相等,但不同之处在于阿基米德多面体的每个面的形状不全相同.有几种阿基米德多面体可由正多面体进行“截角”得到如图,正八面体的棱长为3,取各条棱的三等分点,截去六个角后得到一种阿基米德多面体,则该阿基米德多面体( )
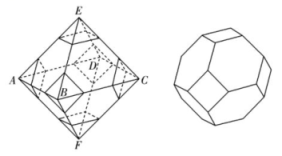 A、共有18个顶点 B、共有36条棱 C、表面积为 D、体积为11. 已知函数 , 则( )A、曲线在点处的切线方程为 B、函数的极小值为 C、当时,仅有一个整数解 D、当时,仅有一个整数解
A、共有18个顶点 B、共有36条棱 C、表面积为 D、体积为11. 已知函数 , 则( )A、曲线在点处的切线方程为 B、函数的极小值为 C、当时,仅有一个整数解 D、当时,仅有一个整数解三、填空题(每题5分,共15分)
-
12. 某公司新成立3个产品研发小组,公司选派了5名专家对研发工作进行指导.若每个小组至少有一名专家且5人均要派出,若专家甲、乙需到同一个小组指导工作,则不同的专家派遣方案总数为.(用数字作答)13. 在中, D为AC上一点且满足 若P为BD的中点,且满足 则的值是.14. 古希腊著名数学家阿波罗尼斯与欧几里得、阿基米德齐名,他发现:平面内到两个定点 , 的距离之比为定值(且)的点所形成的图形是圆,后来,人们把这个圆以他的名字命名,称为阿波罗尼斯圆,简称阿氏圆.已知点到两个定点 , 的距离之比为2,则的取值范围为.
四、解答题(共5题,共77分)
-
15. 某市为了了解校园安全教育系列活动的成效,对全市高中生进行一次安全意识测试,根据测试成绩评定“合格”、“不合格”两个等级,同时对相应等级进行量化,现随机抽取部分高中生的答卷,统计结果如下,对应的频率分布直方图如图所示.

等级
不合格
合格
得分
频数
12
48
24
(1)、求的值;(2)、估计该市高中生测试成绩评定等级为“合格”的概率;(3)、在抽取的答卷中,用分层抽样的方法,从评定等级为“合格”和“不合格”的答卷中抽取5份,再从这5份答卷中任取2份,求恰有1份评定等级为“不合格”的概率16. 设数列的前项和为 , 已知 , 是公差为的等差数列.(1)、求的通项公式;(2)、设 , 求数列的前项和 .

