2024年人教A版高一下学期数学期中模拟试卷二(范围:必修一,必修二8.4)
试卷更新日期:2024-04-22 类型:期中考试
一、选择题(每题5分,共40分)
-
1. 命题“ , ”的否定是( )A、 , B、 , C、 , D、 ,2. 已知为实数,复数为纯虚数,则( )A、-1 B、1 C、-2 D、23. 下列说法不正确的是( )A、直四棱柱是长方体 B、正方体是平行六面体 C、长方体是平行六面体 D、平行六面体是四棱柱4. 判断下列各命题的真假:①向量与平行,则与的方向相同或相反;②两个有共同起点而且相等的向量,其终点必相同;③零向量是没有方向的;④向量就是有向线段.其中假命题的个数为( )A、2 B、3 C、4 D、55. 在中,(分别为角的对边),则的形状可能是( )A、正三角形 B、直角三角形 C、等腰直角三角形 D、等腰三角形6. 已知圆台上下底面半径之比为 , 母线与底面所成的角的正弦值为 , 圆台体积为 , 则该圆台的侧面面积为( )A、 B、 C、 D、7. 我国南宋著名数学家秦九韶提出了由三角形三边求三角形面积的“三斜求积”,设的三个内角所对的边分别为 , , , 面积为S , 则“三斜求积”公式为若 , , 则用“三斜求积”公式求得的面积为( )A、 B、 C、 D、18. 若函数在区间上单调递增,则实数的取值范围是( )A、 B、 C、 D、
二、多项选择题(每题5分,共20分)
-
9. 下列说法正确的有( )A、已知 , , 若与共线,则 B、若 , , 则 C、若 , 则一定不与共线 D、若 , , 为锐角,则实数的范围是10. 已知函数其中 , , 的部分图象如图所示,则下列结论正确的是( )
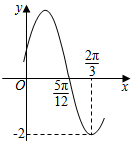 A、函数的图象关于点对称
A、函数的图象关于点对称
B、函数的图象关于直线对称
C、函数在区间上单调递增
D、与图象的所有交点的横坐标之和为
11. 在中,内角A,B,C所对的边分别为a,b,c,且 , 则下列选项正确的是( )A、若 , 则有两解 B、若 , 则无解 C、若为锐角三角形,且 , 则 D、若 , 则的最大值为12. 已知函数 , 若方程有四个不同的零点 , 且 , 则下列结论正确的是( )A、 B、 C、 D、三、填空题(每题5分,共20分)
-
13. 设 , , 若 , 则 .14. 已知函数的定义域为 , 则函数的定义域为 .15. 已知正方形ABCD的边长为2,E为CD的中点,点F在AD上, , 则.16. 一个正四棱锥底面边长为2,高为 , 则该四棱锥的内切球表面积为.
四、解答题(共6题,共71分)
-
17. 已知复数 , , 其中i为虚数单位,且满足 , 且为纯虚数.(1)、若复数 , 在复平面内对应点在第一象限,求复数z;(2)、求;(3)、若在(1)中条件下的复数z是关于x的方程的一个根,求实数m , n的值.18. 设a , b , c分别为内角A , B , C的对边,已知 , .(1)、求A的值;(2)、若 , , 求c的值.19. 如图,某铁质零件由一个正三棱台和一个正三棱柱组成,已知正三棱柱的底面边长与高均为1cm,正三棱台的下底面边长为2cm,且正三棱台的高为1cm,现有一盒这种零件共重(不包含盒子的质量),取铁的密度为 .
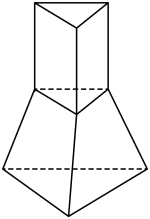 (1)、试问该盒中有多少个这样的零件?(2)、如果要给这盒零件的每个零件表面涂上一种特殊的材料,试问共需涂多少的材料?
(1)、试问该盒中有多少个这样的零件?(2)、如果要给这盒零件的每个零件表面涂上一种特殊的材料,试问共需涂多少的材料?
