2024年中考数学真题改编贵州模拟试卷(四)
试卷更新日期:2024-04-22 类型:中考模拟
一、选择题
-
1. 计算的结果是( )A、6 B、 C、5 D、2. 下列4个袋子中,装有除颜色外完全相同的10个小球,任意摸出一个球,摸到红球可能性最大的是( )
A、 B、
B、 C、
C、 D、
D、 3. 某班的体训队员的身高(单位:cm)如下:169,165,166,164,169,167,166,169,166,165.获得这组数据的方法是( )A、直接观察 B、查阅文献资料 C、互联网查询 D、测量4. 如图,直线 , 相交, , 则( )
3. 某班的体训队员的身高(单位:cm)如下:169,165,166,164,169,167,166,169,166,165.获得这组数据的方法是( )A、直接观察 B、查阅文献资料 C、互联网查询 D、测量4. 如图,直线 , 相交, , 则( )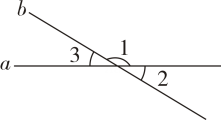 A、
A、
B、
C、
D、5. 当x=1时,下列分式中,没有意义的是( )A、 B、 C、 D、6. 下列计算正确的是( )A、a2+a4=a6 B、 C、(-a2)3=a6 D、(a-b)(b+a)=b2-a27. 如图,A,B,C是⊙O上的三点,∠ABO=25°,∠ACO=30°,则∠BOC的度数为( ) A、100° B、110° C、125° D、130°8. 如图所示,表示两棵小树在同一时刻阳光下的影子的图形可能是( )A、
A、100° B、110° C、125° D、130°8. 如图所示,表示两棵小树在同一时刻阳光下的影子的图形可能是( )A、 B、
B、 C、
C、 D、
D、 9. 已知菱形的周长为20,其中一条对角线的长为8,则另一条对角线的长为( )A、3 B、4 C、6 D、810. 若 , 则下列不等式一定成立的是( )A、 B、 C、 D、11. 尺规作图作的平分线的方法如下:
9. 已知菱形的周长为20,其中一条对角线的长为8,则另一条对角线的长为( )A、3 B、4 C、6 D、810. 若 , 则下列不等式一定成立的是( )A、 B、 C、 D、11. 尺规作图作的平分线的方法如下:如图,以点为圆心,任意长为半径作弧,交 , 于点 , , 再分别以点 , 为圆心,以大于长为半径作弧,两弧交于点 , 作射线由作法得到的根据是.( )
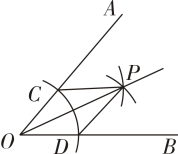 A、 B、 C、 D、12. 已知二次函数的图象如图所示,给出以下结论:①;②;③;④;⑤ , 其中正确结论是( )
A、 B、 C、 D、12. 已知二次函数的图象如图所示,给出以下结论:①;②;③;④;⑤ , 其中正确结论是( ) A、②③④ B、②③⑤ C、①②⑤ D、①③⑤
A、②③④ B、②③⑤ C、①②⑤ D、①③⑤二、填空题
-
13. 分解因式:x2y﹣y= .14. 任意抛掷一只纸杯200次,经过统计发现“杯口朝上”的次数为48次,则由此可以估计这只纸杯出现“杯口朝上”的概率为 .15. 如图所示,P为反比例函数y=的图象上的点,过P分别向x轴和y轴引垂线,它们与两条坐标轴围成的矩形面积为2,这个反比例函数表达式为.
 16. 对于每个正整数n , 设表示的末位数字,例如:(的末位数字),(的末位数字),(的末位数字)…,则的值是( )A、 B、 C、 D、
16. 对于每个正整数n , 设表示的末位数字,例如:(的末位数字),(的末位数字),(的末位数字)…,则的值是( )A、 B、 C、 D、三、解答题
-
17.(1)、计算:;(2)、解不等式组:18. 如图,矩形的对角线交于点F , 延长到点C , 使 , 延长到点D , 使 , 连接
 (1)、求证:四边形是菱形;(2)、若 , 求菱形的面积.19. 一个羽毛球的质量合格标准是5.0~5.2g(含5.0g,不含5.2g),某厂对4月生产的羽毛球质量进行抽样检验,并将所得数据绘制成如图所示的统计图(不完整)和统计表.
(1)、求证:四边形是菱形;(2)、若 , 求菱形的面积.19. 一个羽毛球的质量合格标准是5.0~5.2g(含5.0g,不含5.2g),某厂对4月生产的羽毛球质量进行抽样检验,并将所得数据绘制成如图所示的统计图(不完整)和统计表.
4月生产的羽毛球质量统计表
4月生产的羽毛球质量扇形统计图组别 质量x(g) 数量(个) A x<5.0 m B 5.0≤x<5.1 400 C 5.1≤x<5.2 550 D x≥5.2 30  (1)、求表中 m的值及图中B组所在扇形的圆心角的度数.(2)、这些抽样检验的羽毛球中,合格率是多少?如果购得4月生产的羽毛球10简(每筒12 个),估计所购得的羽毛球中,不合格的羽毛球有多少个?20. 如图,已知 , 是一次函数的图象和反比例函数的图象的两个交点.
(1)、求表中 m的值及图中B组所在扇形的圆心角的度数.(2)、这些抽样检验的羽毛球中,合格率是多少?如果购得4月生产的羽毛球10简(每筒12 个),估计所购得的羽毛球中,不合格的羽毛球有多少个?20. 如图,已知 , 是一次函数的图象和反比例函数的图象的两个交点.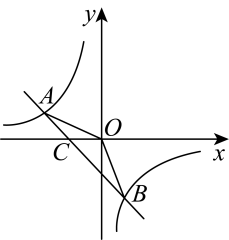 (1)、求反比例函数和一次函数的解析式;(2)、求的面积;(3)、求不等式的解集(请直接写出答案).21. 如图,某数学小组测量街阳三塔之一“来雁塔”的高度,在坡底D处测得测得塔顶A的仰角为 , 沿坡比为的斜坡前行26米到达平台C处,在C处测得塔顶A的仰角为
(1)、求反比例函数和一次函数的解析式;(2)、求的面积;(3)、求不等式的解集(请直接写出答案).21. 如图,某数学小组测量街阳三塔之一“来雁塔”的高度,在坡底D处测得测得塔顶A的仰角为 , 沿坡比为的斜坡前行26米到达平台C处,在C处测得塔顶A的仰角为 (1)、求坡顶C到地面的距离:(2)、计算来雁塔的高度.22. 某中学计划购买A型和型课桌凳共200套,经招标,购买一套型课桌凳比购买一套型课桌凳少用40元,且购买3套型和5套型课桌凳共需1640元.(1)、求购买一套型课桌凳和一套型课桌凳各需多少元?(2)、学校根据实际情况,要求购买这两种课桌凳的总费用不能超过40880元,并且购买型课桌凳的数量不能超过型课桌凳数量的 , 求该校本次购买型和型课桌凳共有几种购买方案?怎样的方案使总费用最低?并求出最低消费.23. 如图,四边形为的内接四边形,为的直径,且与互余.
(1)、求坡顶C到地面的距离:(2)、计算来雁塔的高度.22. 某中学计划购买A型和型课桌凳共200套,经招标,购买一套型课桌凳比购买一套型课桌凳少用40元,且购买3套型和5套型课桌凳共需1640元.(1)、求购买一套型课桌凳和一套型课桌凳各需多少元?(2)、学校根据实际情况,要求购买这两种课桌凳的总费用不能超过40880元,并且购买型课桌凳的数量不能超过型课桌凳数量的 , 求该校本次购买型和型课桌凳共有几种购买方案?怎样的方案使总费用最低?并求出最低消费.23. 如图,四边形为的内接四边形,为的直径,且与互余.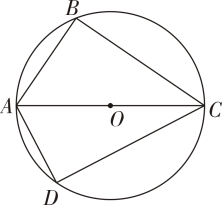 (1)、求证:;(2)、若 , , 求的长.24. 已知二次函数y=x2+bx+c经过A(1,1)和B(-1,-3),二次函数与一次函数y=-x-2交于C , D两点.(1)、求二次函数的解析式.(2)、求三角形BCD的面积.(3)、结合图象直接写出不等式x2+bx+c>-x-2的解集.25. 通过类比联想、引申拓展研究典型题目,可达到解一题知一类的目的.下面是一个案例,请补充完整.
(1)、求证:;(2)、若 , , 求的长.24. 已知二次函数y=x2+bx+c经过A(1,1)和B(-1,-3),二次函数与一次函数y=-x-2交于C , D两点.(1)、求二次函数的解析式.(2)、求三角形BCD的面积.(3)、结合图象直接写出不等式x2+bx+c>-x-2的解集.25. 通过类比联想、引申拓展研究典型题目,可达到解一题知一类的目的.下面是一个案例,请补充完整.
原题:如图1,点E , F分别在正方形ABCD的边BC , CD上,∠EAF=45°,连接EF , 则EF=BE+DF , 试说明理由.
(1)、思路梳理∵AB=CD , ∴把△ABE绕点A逆时针旋转90°至△ADG , 可使AB与AD重合.∵∠ADC=∠B=90°∠FDG=180°,∴点F , D , G共线.根据(从“SSS , ASA , AAS , SAS”中选择填写),易证△AFG≌ , 得EF=BE+DF .
(2)、类比引申如图2,四边形ABCD中,AB=AD , ∠BAD=90°,点E , F分别在边BC , CD上,∠EAF=45°.若∠B , ∠D都不是直角,则当∠B与∠D满足等量关系时,仍有EF=BE+DF .
(3)、联想拓展如图3,在△ABC中,∠BAC=90°,AB=AC , 点D , E均在边BC上,且∠DAE=45°.猜想BD , DE , EC应满足的等量关系,并写出推理过程.
(4)、思维深化如图4,在△ABC中,∠BAC=60°,AB=AC , 点D , E均在直线BC上,点D在点E的左边,且∠DAE=30°,当AB=4,BD=1时,直接写出CE的长.