2024年中考数学真题改编贵州模拟试卷（五）

试卷更新日期：2024-04-22 类型：中考模拟

进入出卷网下载

一、选择题

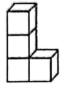
1. 乘方4³等于（　　）

A、4×4×4 B、3×3×3×3 C、3×4 D、4+4+4

查看试题解析
2. 如图是一个由4个相同的正方体组成的立体图形，从上面看得到的平面图形是（）

A、 B、 C、 D、

查看试题解析
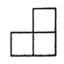3. 下列式子不能用平方差公式计算的是（）

A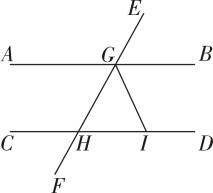、 $(a + b) (a - b)$ B、 $(- x + 1) (- x - 1)$ C、 $(y + 1) (- y - 1)$ D、 $(m - 1) (- 1 - m)$

查看试题解析
4. 如图，若 $∠ E G B = ∠ C H F = 58 °$ ， $G I$ 平分 $∠ B G F$ ，则 $∠ G I D$ 等于（）

A、 $122 °$
B、 $116 °$
C、 $119 °$
D、 $120 °$

查看试题解析
5. 如图，已知 $△ A B C$ 中， $A B = A C$ ，点D在底边BC上，添加下列条件后，仍无法判定 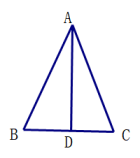$△ A B D ≌ △ A C D$ 的是（）

A、 $B D = C D$ B、 $∠ B A D = ∠ C A D$ C、 $∠ B = ∠ C$ D、 $∠ B = ∠ C$ ， $∠ A D B = ∠ A D C$

查看试题解析
6. 如图，一块飞镖游戏板由大小相等的小正方形格子构成，向游戏板随机投掷一枚飞镖，击中黑色区域的概率是（　　）

A、 $\frac{5}{9}$ B、 $\frac{1}{3}$ C、 $\frac{5}{18}$ D、 $\frac{2}{3}$

查看试题解析
7. 如图，菱形ABCD中，AC＝8．BD＝6．则菱形的面积为（）

A、20 B、40 C、28 D、24

查看试题解析
8. 如图，五边形 $A B C D E$ 是 $⊙ O$ 的内接正五边形， $A F$ 是 $⊙ O$ 的直径，则 $∠ B D F$ 的度数是（）

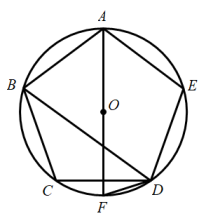A、18° B、36° C、 $54 °$ D、72°

查看试题解析
9. 某中学开展“阳光体育一小时”活动，根据学校实际情况，决定开设①踢毽子；②篮球；③跳绳；④乒乓球四种运动项目．为了解学生最喜欢哪一种运动项目，随机抽取了一部分学生进行调查，并将调查结果绘制成如下不完整的两个统计图，依据图中信息，得出下列结论中正确的是（）

A、本次共调查300名学生 B、扇形统计图中，喜欢篮球项目的学生部分所对应的扇形圆心角大小为45° C、喜欢跳绳项日的学生人数为60人 D、喜欢篮球项目的学生人数为30人

查看试题解析
10. 已知线段 $A B = 10 c m$ ，线段 $A C = 16 c m$ ，且 $A B$ 、 $A C$ 在同一条直线上，点 $B$ 在 $A$ 、 $C$ 之间，此时 $A B$ 、 $A C$ 的中点 $M$ 、 $N$ 之间的距离为（）

A、13cm B、6cm C、3cm D、1.5cm

查看试题解析
11. 如图，在Rt△ABC中，∠ACB=90°，根据尺规作图的痕迹判断，以下结论中错误的是（）

A、∠BDE=∠BAC B、∠BAD=∠B C、DE=DC D、AE=AC

查看试题解析
12. 一次函数y₁=mx+n(m≠0)与二次函数y₂=ax²+bx+c(a≠0)的图象如图所示，则不等式ax²+bx+c>mx+n的解集为（）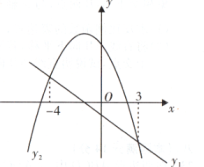

A、-4<x<3 B、x<-4 C、3-<<x<-4 D、x>3或x<-4

查看试题解析

二、填空题

13. 若分式 $\frac{x^{2} - 9}{x - 3}$ 的值为零，则x的值为．

查看试题解析
14. 在不透明的盒子中装有一个黑球，两个白球，三个红球，四个绿球，这十个球除颜色外完全相同．那么从中随机摸出一个球是绿球的概率为．

查看试题解析
15. 如图，已知函数 $y = 2 x + b$ 与函数 $y = k x - 3$ 的图象交于点 $P$ ，则方程组 ${\begin{array}{l} 2 x - y = - b \\ k x - y = 3 \end{array}$ 的解是．

查看试题解析
16. 如图，正方形 $A B C D$ 的边长为4，点E是正方形外一动点，且点E在 $C D$ 的右侧， $∠ A E D = 45 °$ ， P为 $A B$ 的中点，当E运动时，线段 $P E$ 的最大值为.

查看试题解析

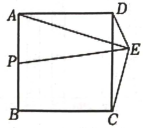
三、解答题

17.

(1)、计算： $\sqrt{12} - 4 | Unsupported character s i n 6 0^{°} | + {(\frac{1}{3})}^{- 1} - (2023 - π)^{0}$ ；

(2)、先化简，再求值： $(1 + \frac{3}{x - 5}) \div \frac{x^{2} - 4 x + 4}{2 x - 10}$ ，其中 $x = \sqrt{2} + 2$

查看试题解析
18. 如图，矩形 $A E B O$ 的对角线 $A B ， O E$ 交于点F ，延长 $A O$ 到点C ，使 $O C = O A$ ，延长 $B O$ 到点D ，使 $O D = O B$ ，连接 $A D ， D C ， B C ．$

(1)、求证：四边形 $A B C D$ 是菱形；

(2)、若 $O E = 10 ， ∠ B C D = 60 °$ ，求菱形 $A B C D$ 的面积．

查看试题解析
19. 为了解出租车司机的收入情况，某校七年级数学兴趣小组从甲、乙两家出租车公司分别随机抽取10名司机的月收入（单位：千元）进行统计，其情况如表：
甲公司司机月收入情况

月收入（千元）
4
5
6
7
8
人数（名）
1
2
4
2
1
乙公司司机月收入情况

月收入（千元）
4
5
9
12
人数（名）
5
2
2
1
根据以上信息，整理分析数据如表：


平均数
中位数
众数
甲公司司机月收入（千元）
6
a
b
乙公司司机月收入（千元）
c
d
4

(1)、填空：a＝， b＝， c＝， d＝；

(2)、若甲公司将出租车换成新能源汽车，运营成本下降，每个司机的月收入都增加了1千元，则甲公司司机月收入的方差会（填“变大”，“变小”或“不变”）；

(3)、某人决定从两家公司中选择一家应聘出租车司机，你建议他选哪家公司？简述理由．

查看试题解析
20. 常德市某校购进一批甲、乙两种中考排球，已知一只甲种排球的价格与一只乙种排球的价格的和为40元，用900元购进甲种排球的件数与用1500元购进乙种排球的件数相同．

(1)、求每件甲种、乙种排球的价格分别是多少元？

(2)、该校计划用3500元购买甲、乙两种排球，由于采购人员把甲、乙两种排球的只数互换了，结果需4500元，求该校原计划购进甲、乙两种排球各多少只？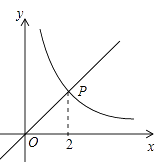

查看试题解析
21. 如图，函数 $y = x$ 的图象与函数 $y = \frac{k}{x} (x > 0)$ 的图象相交于点 $P (2 ， m)$ .

(1)、求 $m$ ， $k$ 的值；

(2)、直线 $y = 4$ 与函数 $y = x$ 的图象相交于点 $A$ ，与函数 $y = \frac{k}{x} (x > 0)$ 的图象相交于点 $B$ ，求线段 $A B$ 长.

查看试题解析
22. 我国于2019年6月5日首次完成运载火箭海上发射，达到了发射技术的新高度．如图，运载火箭海面发射站点M与岸边雷达站N处在同一水平高度．当火箭到达点A处时，测得点A距离发射站点M的垂直高度为9千米，雷达站N测得A处的仰角为 $37 °$ ，火箭继续垂直上升到达点B处，此时海岸边N处的雷达测得B处的仰角为 $70 °$ ，根据下面提供的参考数据计算下列问题∶

(1)、求火箭海面发射站点M与岸边雷达站N的距离；

(2)、求火箭所在点B处距发射站点M处的高度．
（参考数据∶ $\sin 70 ° \approx 0.94$ ， $\cos 70 ° \approx 0.34$ ， $\tan 70 ° \approx 2.75$ ， $\sin 37 ° \approx 0.6$ ， $\cos 37 ° \approx 0.80$ ， $\tan 37 ° \approx 0.75$ ）

查看试题解析
23. 如图，△ABD是⊙O的内接三角形，E是弦BD的中点，点C是⊙O外一点且∠DBC=∠A，连接OE延长与圆相交于点F，与BC相交于点C．

(1)、求证：BC是⊙O的切线；

(2)、若⊙O的半径为6，BC=8，求弦BD的长．

查看试题解析
24. 如图，二次函数 $y = x^{2} - 3 x + c$ 的图象与 $x$ 轴的一个交点为 $A (4 ， 0)$ ，另一个交点为 $B$ ，且与 $y$ 轴交于点 $C$ ．

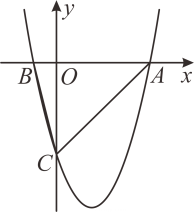(1)、求二次函数的解析式；

(2)、求 $△ A B C$ 的面积；

(3)、该二次函数图象上是否存在点 $D$ ，使 $△ A B D$ 与 $△ A B C$ 的面积相等？若存在，请求出 $D$ 点的坐标；若不存在，请说明理由．

查看试题解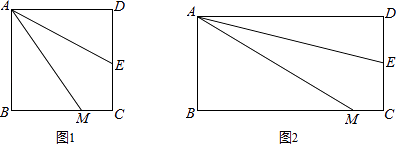析
25.
探究题
【问题情境】
如图1，四边形ABCD是正方形，M是BC边上的一点，E是CD边的中点，AE平分∠DAM．

(1)、【探究展示】

直接写出AM、AD、MC三条线段的数量关系：；

(2)、【拓展延伸】

AM=DE+BM是否成立？若成立，请给出证明；若不成立，请说明理由．

(3)、若四边形ABCD是长与宽不相等的矩形，其他条件不变，如图2，探究展示（1）、（2）中的结论是否成立？请分别作出判断，不需要证明．

查看试题解析

	平均数	中位数	众数
甲公司司机月收入（千元）	6	a	b
乙公司司机月收入（千元）	c	d	4

月收入（千元）	4	5	6	7	8
人数（名）	1	2	4	2	1

月收入（千元）	4	5	9	12
人数（名）	5	2	2	1