备考2024年中考数学计算能力训练3 整式的运算

试卷更新日期：2024-04-21 类型：二轮复习

进入出卷网下载

一、选择题

1. 计算 $(- x^{2})^{3}$ 的结果是（）

A、 $- x^{6}$ B、 $x^{6}$ C、 $- x^{5}$ D、 $- x^{8}$

查看试题解析
2. 下列计算正确的是（）

A、 $x^{7} \div x ＝ x^{7}$ B、 ${(- 3 x^{2})}^{2} = - 9 x^{4}$ C、 $x^{3} • x^{3} ＝ 2 x^{6}$ D、 $（ x^{3} ）^{2} ＝ x^{6}$

查看试题解析
3. 下列计算正确的是（　　）

A、3x+3y=6xy B、a²•a³=a⁶ C、b⁶÷b³=b² D、（m²）³=m⁶

查看试题解析
4. 下列计算正确的是（）

A、 $3 a^{3} \cdot 2 a^{3} = 6 a^{3}$ B、 $(- 4 a^{3} b)^{2} = 8 a^{6} b^{2}$ C、 $(a + b)^{2} = a^{2} + b^{2}$ D、 $- 2 a^{2} + 3 a^{2} = a^{2}$

查看试题解析
5. 下列运算正确的是（）

A、 $(x - 1) (x + 1) = x^{2} - x - 1$ B、 $x^{2} - 2 x + 3 = {(x - 1)}^{2} + 4$ C、 ${(x - 1)}^{2} = x^{2} - 2 x - 1$ D、 $(x - 1) (- 1 - x) = 1 - x^{2}$

查看试题解析
6. 观察一列单项式：x ， $- 3 x^{3}$ ， $7 x^{5}$ ， $- 15 x^{7}$ ， $31 x^{9}$ ， ⋯．则第n个单项式是（）

A、 $(- 1)^{n + 1} (2 n - 1) x^{2 n - 1}$ B、 $(- 1)^{n} (2^{n} - 1) x^{2 n + 1}$ C、 $(- 1)^{n + 1} (2^{n} - 1) x^{2 n - 1}$ D、 $(- 1)^{n} (2^{n} + 1) x^{2 n - 1}$

查看试题解析
7. 若k为任意整数，则 $(2 k + 3)^{2} - 4 k^{2}$ 的值总能（）

A、被2整除 B、被3整除 C、被5整除 D、被7整除

查看试题解析
8. 已知 $1 0^{a} = 25, 10 0^{b} = 40$ ，则 $a + 2 b$ 的值是（）

A、1 B、2 C、3 D、4

查看试题解析
9. 对于任意自然数n ，关于代数式（n+7）²﹣（n﹣5）²的值，说法错误的是（　　）

A、总能被3整除 B、总能被4整除 C、总能被6整除 D、总能被7整除

查看试题解析
10. 若2a-3b=-1，则代数式 $4 a^{2} - 12 a b + 9 b^{2}$ 的值为（）

A、-1 B、1 C、2 D、3

查看试题解析
11. 已知关于 $x$ 的两个多项式 $A = x^{2} - a x - 2$ ， $B = x^{2} - 2 x - 3$ ．其中a为常数，下列说法：
①若 $A - B$ 的值始终与 $x$ 无关，则 $a = - 2$ ；
②关于x的方程 $A + B = 0$ 始终有两个不相等的实数根；
③若 $A \cdot B$ 的结果不含 $x^{2}$ 的项，则 $a = \frac{5}{2}$ ；
④当 $a = 1$ 时，若 $\frac{A}{B}$ 的值为整数，则x的整数值只有2个．
以上结论正确的个数有（）

A、4 B、3 C、2 D、1

查看试题解析
12. 对于若干个单项式，我们先将任意两个单项式作差，再将这些差的绝对值进行求和并化简，这样的运算称为对这若干个单项式作“差绝对值运算”．例如：对 $2 ， 3 ， 4$ 作“差绝对值运算”，得到 $| 2 - 3 | + | 2 - 4 | + | 3 - 4 | = 4$ ，则
$①$ 对 $1 ， 3 ， 4 ， 7$ 作“差绝对值运算”的结果是 $19$ ； $②$ 对 $x^{2} ， x ， - 3 (x^{2} > x > - 3)$ 进行“差绝对值运算”的结果是 $38$ ，则 $x = \pm 4$ ； $③$ 对 $a ， b ， c$ （互不相等）进行“差绝对值运算”的结果一共有 $7$ 种．
以上说法中正确的个数为（）

A、 $0$ B、 $1$ C、 $2$ D、 $3$

查看试题解析

二、填空题

13. 已知3x+y=-3， xy=-6，则 $x y^{3} + 9 x^{3} y$ =.

查看试题解析
14. 若实数m满足 ${(m - 2023)}^{2} + {(2024 - m)}^{2} = 2025$ ，则 $(m - 2023) (2024 - m) =$ ．

查看试题解析
15. 已知 $m + n + \frac{2}{m + n} = 4 ，$ 则 ${(m + n)}^{2} + {(\frac{2}{m + n})}^{2}$ 的值为.

查看试题解析
16. 小明在化简： $(4 x^{2} - 6 x + 7) - (4 x^{2} - □ x + 2)$ 时发现系数“□”印刷不清楚，老师提示他：“此题的化简结果是常数”，则多项式中的“□”表示的数是.

查看试题解析
17. 如果一个三位自然数 $m = \bar{a b c}$ 的各数位上的数字互不相等且均不为0，满足 $a + c = b$ ，那么称这个三位数为“中庸数”．将“中庸数” $m = \bar{a b c}$ 的百位、个位数字交换位置，得到另一个“中庸数” $m^{'} = \bar{c b a}$ ，记 $F (m) = \frac{m - m^{'}}{99} ， T (m) = \frac{m + m^{'}}{121}$ ．例如： $m = 792 ， m^{'} = 297$ ． $F (m) = \frac{792 - 297}{99} = 5$ ， $T (m) = \frac{792 + 297}{121} = 9$ ．计算 $F (583) =$ ；若“中庸数” $m$ 满足 $2 F (m) = s^{2} ， 2 T (m) = t^{2}$ ，其中 $s ， t$ 为自然数1，2，3……，则该“中庸数” $m$ 是．

查看试题解析
18. 一个四位自然数M，若它的千位数字与十位数字的差为3，百位数字与个位数字的差为2，则称M为“接二连三数”，则最大的“接二连三数”为；已知“接二连三数”M能被9整除，将其千位数字与百位数字之和记为P，十位数字与个位数字之差记为Q，当 $\frac{P}{Q}$ 为整数时，满足条件的M的最小值为．

查看试题解析

三、计算题

19. 计算：

(1)、 $x (1 - x)$ ；

(2)、 $(a - 1) (2 a + 3) - 2 a (a - 4)$ ；

(3)、 $\frac{x^{2}}{x - 1} - x - 1$ ．

查看试题解析
20. 计算：

(1)、 ${(- 2 x y^{2})}^{2} \cdot 3 x^{2} y$ ．

(2)、 $(- 2 a^{2}) (3 a b^{2} - 5 a b^{3})$ ．

(3)、 ${(3 m^{2} n)}^{2} \cdot {(- 2 m^{2})}^{3} \div {(- m^{2} n)}^{2}$ ．

(4)、 $(a - 2 b - 3 c) (a - 2 b + 3 c)$ ．

查看试题解析
21. （x+2）²+（2x+1）（2x﹣1）﹣4x（x+1），其中x＝ $- \frac{1}{2}$ .．

查看试题解析
22. $- \frac{1}{2} (x y - x^{2}) + 3 (y^{2} - \frac{1}{2} x^{2}) + 2 (\frac{1}{4} x y - \frac{1}{2} y^{2})$ ，其中 $x = - 2$ ， $y = \frac{1}{2}$ ．

查看试题解析
23. 先化简，再求值： $[{(x + 2 y)}^{2} - (x + 2 y) (x - 2 y)] \div 4 y$ ，其中 $x = 1$ ， $y = - 1$ ．

查看试题解析

四、解答题

24. 观察下面的等式： $3^{2} - 1^{2} = 8 \times 1 ， 5^{2} - 3^{2} = 8 \times 2 ， 7^{2} - 5^{2} = 8 \times 3 ， 9^{2} - 7^{2} = 8 \times 4 ， ⋯$

(1)、写出 $1 9^{2} - 1 7^{2}$ 的结果．

(2)、按上面的规律归纳出一个一般的结论（用含n的等式表示，n为正整数）

(3)、请运用有关知识，推理说明这个结论是正确的．

查看试题解析
25. 尝试：① $1 5^{2} = 225 = 1 \times 2 \times 100 + 25$ .
② $2 5^{2} = 625 = 2 \times 3 \times 100 + 25$ .
③ $3 5^{2} = 1225 =$ _▲_
...
运用：小滨给出了猜想和证明，请判断是否正确，若有错误请给出正确解答.
猜想： $(10 a + 5)^{2} = 100 a (a + 1) + 25$ .
证明： $(10 a + 5)^{2} = 100 a (a + 1) + 25$ ，
所以 $10 a^{2} + 100 a + 5 = 100 a^{2} + 100 a + 25$ .
所以 $10 a^{2} = 100 a^{2}$ .
因为 $a \neq 0$ ，
所以 $10 a^{2} \neq 100 a^{2}$ .
所以等式不成立，结论错误.

查看试题解析
26. 已知实数a、b满足（2a²+b²+1）（2a²+b²-1）＝80，试求2a²+b²的值．解：设2a²+b²＝m ，则原方程可化为（m+1）（m-1）＝80，即m²＝81，解得：m＝±9，∵2a²+b²≥0，∴2a²+b²＝9，上面的这种方法称为“换元法”，换元法是数学学习中最常用的一种思想方法，在结构较复杂的数和式的运算中，若把其中某些部分看成一个整体，并用新字母代替（即换元），则能使复杂问题简单化．根据以上阅读材料，解决下列问题：

(1)、已知实数x、y满足（2x²+2y²-1）（x²+y²）＝3，求3x²+3y²-2的值；

(2)、若四个连续正整数的积为120，求这四个正整数．

查看试题解析
27. 阅读下列材料：
我们把多项式a²+2ab+b²及a²-2ab+b²叫做完全平方公式，如果一个多项式不是完全平方公式，我们常做如下变形：先添加一个适当的项，使式子中出现完全平方式，再减去这个项，使整个式子的值不变，这种方法叫做配方法．配方法是一种重要的解决问题的数学方法，可以求代数式的最大值或最小值．
例如：求代数式x²+2x-3的最小值．
解：x²+2x-3＝x²+2x+1²-1²-3＝（x²+2x+1²）-4＝（x+1）²-4．
∵（x+1）²≥0，∴（x+1）²-4≥-4，
∴当x＝-1时，x²+2x-3的最小值为-4．
再例如：求代数式-x²+4x-1的最大值．
解：-x²+4x-1＝-（x²-4x+1）＝-（x²-4x+2²-2²+1）
＝-[（x²-4x+2²）-3]＝-（x-2）²+3
∵（x-2）²≥0，∴-（x-2）²≤0，∴-（x-2）²+3≤3．
∴当x＝2时，-x²+4x-1的最大值为3．

(1)、【直接应用】代数式x²+4x+3的最小值为；

(2)、【类比应用】若M＝a²+b²-2a+4b+2023，试求M的最小值；

(3)、【知识迁移】如图，学校打算用长20m的篱笆围一个长方形菜地，菜地的一面靠墙（墙足够长），求围成的菜地的最大面积．

查看试题解析
28. 在学习《完全平方公式》时，某数学学习小组发现：已知a+b＝5，ab＝3，可以在不求a、b的值的情况下，求出a²+b²的值．具体做法如下：
a²+b²＝a²+b²+2ab-2ab＝（a+b）²-2ab＝5²-2×3＝19．

(1)、若a+b＝7，ab＝6，则a²+b²＝；

(2)、若m满足（8-m）（m-3）＝3，求（8-m）²+（m-3）²的值，同样可以应用上述方法解决问题．具体操作如下：
解：设8-m＝a，8-m＝a，m-3＝b，
则a+b＝（8-m）+（m-3）＝5，a+b＝（8-m）+（m-3）＝5，ab＝（8-m）（m-3）＝3，
所以（8-m）²+（m-3）²＝a²+b²＝（a+b）²-2ab＝5²-2×3＝19．
请参照上述方法解决下列问题：若（3x-2）（10-3x）＝6，求（3x-2）²+（10-3x）²的值；

查看试题解析
29. 利用完全平方公式 $a^{2} + 2 a b + b^{2} = (a + b)^{2}$ 和 $a^{2} - 2 a b + b =^{2} (a - b)^{2}$ 的特点可以解决很多数学问题 $.$ 下面给出两个例子：
例 $1$ 、分解因式： $x^{2} + 2 x - 3$
$x^{2} + 2 x - 3 = x^{2} + 2 x + 1 - 4 = (x + 1)^{2} - 4 = (x + 1 + 2) (x + 1 - 2) = (x + 3) (x - 1)$
例 $2$ 、求代数式 $2 x^{2} - 4 x - 6$ 的最小值：
$2 x^{2} - 4 x - 6 = 2 (x^{2} - 2 x) - 6 = 2 (x^{2} - 2 x + 1 - 1) - 6 = 2 [(x - 1)^{2} - 1] - 6 = 2 (x - 1)^{2} - 8$
又 $∵ 2 (x - 1)^{2} \geq 0$
$∴$ 当 $x = 1$ 时，代数式 $2 x^{2} - 4 x - 6$ 有最小值，最小值是 $- 8$ ．
仔细阅读上面例题，模仿解决下列问题：

(1)、分解因式： $m^{2} - 8 m + 12$ ；

(2)、代数式 $- x^{2} + 4 x - 2$ 有最 $($ 大、小 $)$ 值，当 $x =$ 时，最值是；

(3)、当 $x$ 、 $y$ 为何值时，多项式 $2 x^{2} + y^{2} - 8 x + 6 y + 25$ 有最小值？并求出这个最小值．

查看试题解析
30. 发现：一个两位数的平方与其个位数字的平方的差，一定是 $20$ 的倍数．如： $1 3^{2} - 3^{2} = 160$ ， $160$ 是 $20$ 的 $8$ 倍； $2 6^{2} - 6^{2} = 640$ ， $640$ 是 $20$ 的 $32$ 倍．

(1)、请你仿照上面的例子，再举出一个例子： $(\cdot \cdot \cdot \cdot)^{2} - (\cdot \cdot \cdot \cdot \cdot)^{2} = (\cdot \cdot \cdot \cdot \cdot)$ ；

(2)、十位数字为1，个位数字为 $a$ 的两位数可表示为，若该两位数的平方与 $a$ 的平方的差是 $20$ 的 $5$ 倍，则 $a =$ ；

(3)、设一个两位数的十位数字为 $m$ ，个位数字为 $n$ （ $0 < m < 10$ ， $0 ≤ n < 10$ ，且 $m$ ， $n$ 为正整数），请用含 $m$ ， $n$ 的式子论证“发现”的结论是否符合题意．

查看试题解析
31. 灵活运用完全平方公式 ${(a \pm b)}^{2} = a^{2} \pm 2 a b + b^{2}$ 可以解决许多数学问题．
例如：已知 $a - b = 3 ， a b = 1$ ，求 $a^{2} + b^{2}$ 的值．
解： $∵ a - b = 3 ， a b = 1$ ， ∴ ${(a - b)}^{2} = 9 ， 2 a b = 2 ， ∴ a^{2} - 2 a b + b^{2} = 9$ ，
$∴ a^{2} - 2 + b^{2} = 9 ， ∴ a^{2} + b^{2} = 9 + 2 = 11$ ．
请根据以上材料，解答下列问题．

(1)、若 $a^{2} + b^{2}$ 与 $2 a b - 4$ 互为相反数，求 $a + b$ 的值．

(2)、如图，矩形的长为a，宽为b，周长为14，面积为8，求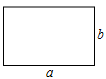 $a^{2} + b^{2}$ 的值．

查看试题解析
32. 定义：对于一个三位正整数，如果十位数字恰好等于百位数字与个位数字之和的一半，我们称这个三位正整数为“半和数”．
例如，三位正整数234，因为 $3 = \frac{1}{2} \times (2 + 4)$ ，所以234是“半和数”．

(1)、判断147是否为“半和数”，并说明理由；

(2)、小林列举了几个“半和数”：111、123、234、840…，并且她发现： $111 \div 3 = 37$ ， $123 \div 3 = 41$ ， $234 \div 3 = 78$ ， $840 \div 3 = 280$ …，所以她猜测任意一个“半和数”都能被3整除．小林的猜想正确吗？若正确，请你帮小林说明该猜想的正确性；若错误，说明理由．

查看试题解析