备考2024年中考数学计算能力训练2 实数的运算
试卷更新日期:2024-04-21 类型:二轮复习
一、选择题
-
1. 下列说法中正确的是( )A、 的值是±5 B、两个无理数的和仍是无理数 C、-3没有立方根. D、 是最简二次根式.2. 实数m,n在数轴上的对应点的位置如图所示,下列结论中正确的是( )
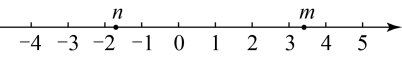 A、 B、 C、 D、3. 计算:等于( )A、-2 B、 C、2 D、04. 观察下列各式: , , , …请利用你所发现的规律,计算 , 其结果为( )A、 B、 C、 D、5. 估计的值应在( )A、和之间 B、和之间 C、和之间 D、和之间.6. 秦兵马俑的发现被誉为“世界第八大奇迹”,兵马俑的眼睛到下巴的距离与头顶到下巴的距离之比为 , 下列各数中最接近于的是( )A、 B、 C、 D、7. 若x为实数,在“”的“”中添上一种运算符号(在“+,-,×,÷”中选择)后,其运算的结果为有理数,则不可能是( )A、 B、 C、 D、8. 计算的结果是( )A、 B、 C、 D、9. 下列运算正确的是()A、 B、 C、 D、10. 今年“十一”期间,广州部分公园举行游园活动,据统计,天河公园早晨时分有人进入公园,接下来的第一个分钟内有人进去人出来,第二个分钟内有人进去人出来,第三个分钟内有人进去人出来,第四个分钟内有人进去人出来.按照这种规律进行下去,到上午时分公园内的人数是( )A、 B、 C、 D、
A、 B、 C、 D、3. 计算:等于( )A、-2 B、 C、2 D、04. 观察下列各式: , , , …请利用你所发现的规律,计算 , 其结果为( )A、 B、 C、 D、5. 估计的值应在( )A、和之间 B、和之间 C、和之间 D、和之间.6. 秦兵马俑的发现被誉为“世界第八大奇迹”,兵马俑的眼睛到下巴的距离与头顶到下巴的距离之比为 , 下列各数中最接近于的是( )A、 B、 C、 D、7. 若x为实数,在“”的“”中添上一种运算符号(在“+,-,×,÷”中选择)后,其运算的结果为有理数,则不可能是( )A、 B、 C、 D、8. 计算的结果是( )A、 B、 C、 D、9. 下列运算正确的是()A、 B、 C、 D、10. 今年“十一”期间,广州部分公园举行游园活动,据统计,天河公园早晨时分有人进入公园,接下来的第一个分钟内有人进去人出来,第二个分钟内有人进去人出来,第三个分钟内有人进去人出来,第四个分钟内有人进去人出来.按照这种规律进行下去,到上午时分公园内的人数是( )A、 B、 C、 D、二、填空题
-
11. .12. 已知),则.13. 计算:=。14. 计算: .15. 计算: .16. 计算: .
三、计算题
-
17. 计算:(1)、sin230°+2sin60°+tan45°+cos230°;(2)、 .18. 计算:19. 计算: .20. 计算: .21. 计算:(1)、(2)、 .
四、综合题
-
22.(1)、在计算时,小亮的计算过程如下:
解:
小莹发现小亮的计算有误,帮助小亮找出了3个错误.请你找出其他错误,参照①~③的格式写在横线上,并依次标注序号:
①;②;③;
请写出正确的计算过程.
(2)、先化简,再求值: , 其中x是方程的根.23. 老师就式子 , 请同学们自己出问题并解答.(1)、小磊的问题:若代表 , 代表 , 计算该式的值.(2)、小敏的问题:若代表 , 代表 , 计算的结果是有理数,求有理数a的值.(3)、小捷的问题:若 , 且和所代表的数是互为相反数,直接写出所代表的数的取值范围.五、实践探究题
-
24. 阅读理解题:
定义:如果一个数的平方等于-1,记为=-1,这个数i叫做虚数单位。那么和我们所学的实数对应起来就叫做复数,表示为(a,b为实数),a叫这个复数的实部,b叫做这个复数的虚部,它的加,减,乘法运算与整式的加,减,乘法运算类似。
例如计算:.
(1)、填空:= , =.(2)、计算:;(3)、试一试:请利用以前学习的有关知识将化简成的形式.25. 阅读理解下面内容,并解决问题.用求差法比较大小
学习了不等式的知识后,我们根据等式和不等式的基本性质,可知比较两个数或式子的大小可以通过求它们的差来判断.如果两个数或式子为m和n,那么
当时,一定有;
当时,一定有;
当时,一定有 .
反过来也符合题意,即
当时,一定有;
当时,一定有;
当时,一定有 .
因此,我们经常把要比较的对象先数量化,再求它们的差,根据差的正负判断对象的大小.这种比较大小的方法被称为“求差法”.
例如:已知 , 比较与的大小.
解:
∵ ,
∴ , , ,
∴ ,
∴ .
“求差法”的实质是把两个数(或式子)的大小判断的问题,转化为一个数(或式子)与0的大小比较的问题.一般步骤为①作差;②变形;③判断符号;④得出结论.
请解决以下问题:
(1)、用“”或“”填空: .(2)、制作某产品有两种用料方案,方案1:用4块A型钢板,6块B型钢板;方案2:用3块A型钢板,7块B型钢板;已知A型钢板的面积比B型钢板的面积大,若A型钢板的面积为x,B型钢板的面积为y,则从省料的角度考虑,应选哪种方案?并说明理由.(3)、已知 , 比较a与的大小.