【培优卷】2024年北师大版数学八（下）5.3分式的加减法同步练习

试卷更新日期：2024-04-21 类型：同步测试

进入出卷网下载

一、选择题

1. 若a ， b互为倒数，则分式 $\frac{a b^{2}}{a - b} + \frac{a^{2} b}{b - a}$ 的值为（　　）

A、1 B、0 C、﹣1 D、﹣2

查看试题解析
2. 已知实数x、y、z满足 $\frac{x}{y + z} + \frac{y}{z + x} + \frac{z}{x + y} = 1$ ，则 $\frac{x^{2}}{y + z} + \frac{y^{2}}{z + x} + \frac{z^{2}}{x + y}$ 的值（）

A、-1 B、0 C、1 D、2

查看试题解析
3. 如图，若x为正整数，则表示1- $\frac{1}{x + 1}$ 的值的点落在（）

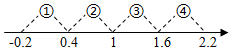A、段① B、段② C、段③ D、段④

查看试题解析
4. 阳阳同学在复习老师已经批阅的作业本时，发现有一道填空题破了一个洞(如图)，则破损部分的式子可能是（）
化简： $(- \frac{3}{1 - x}) \div \frac{x}{x + 1} = \frac{x + 1}{\underline{x - 1}} \sqrt$

A、 $\frac{x - 3}{x - 1}$ B、 $\frac{x + 3}{x - 1}$ C、 $\frac{x^{t} - x + 1}{x^{2} - x}$ D、 $\frac{x^{2} + 5 x + 1}{x^{2} - x}$

查看试题解析
5. 已知：a，b，c三个数满足： $\frac{a b}{a + b} = \frac{1}{2}$ ， $\frac{b c}{b + c} = \frac{1}{3}$ ， $\frac{c a}{c + a} = \frac{1}{4}$ ，则 $\frac{a b c}{a b + b c + a c}$ 的值为（）

A、 $\frac{1}{9}$ B、 $\frac{2}{9}$ C、 $\frac{9}{2}$ D、 $\frac{1}{5}$

查看试题解析
6. 已知当 $x = - 4$ 时，分式 $\frac{x - b}{2 x + a}$ 无意义；当 $x = 2$ 时，此分式的值为0，则 ${(\frac{2 a}{b})}^{2} \cdot \frac{1}{a - b} - \frac{a}{b} \div \frac{b}{4}$ 的值是（）

A、 $\frac{3}{4}$ B、 $\frac{8}{3}$ C、 $\frac{4}{5}$ D、 $\frac{4}{3}$

查看试题解析
7. 已知 $y_{1} = \frac{1}{x - 1}$ ， $y_{2} = \frac{1}{1 - y_{1}}$ ， $y_{3} = \frac{1}{1 - y_{2}}$ ， $y_{4} = \frac{1}{1 - y_{3}}$ ， …， $y_{n} = \frac{1}{1 - y_{n - 1}}$ ，则y₂₀₂₁=（）

A、 $\frac{x - 1}{x - 2}$ B、2-x C、 $\frac{1}{x - 1}$ D、1

查看试题解析
8. 你听说过著名的万有引力定律吗?任何两个物体之间都有引力，如果设两个物体的质量分别为m₁(kg)，m₂(kg)，它们之间的距离为d(m)，那么它们之间的引力就是 $F = \frac{G m_{1} m_{2}}{d^{2}} (N) ，$ 其中G为引力常数.人在地面上所受的重力近似地等于地球对人的引力，此时d就是地球的半径R.天文学家测得地球的半径约占木星半径的 $\frac{4}{45}$ ，地球的质量约占木星质量的 $\frac{3}{318}$ ，则站在地球地面上的人所受的地球重力约是他在木星表面上所受木星重力的（）

A、 $\frac{5}{2}$ 倍 B、 $\frac{2}{5}$ 倍 C、25倍 D、 $\frac{1}{4}$ 倍

查看试题解析

二、填空题

9. 若 $a^{3} + 3 a^{2} + a = 0$ ，则 $\frac{2023 a^{2}}{a^{4} - 2023 a^{2} + 1} =$ ．

查看试题解析
10. 已知 $x$ ， $y$ ， $z$ ， $a$ ， $b$ 均为非零实数，且满足 $\frac{x y}{x + y} = \frac{1}{a^{3} - b^{3}} ， \frac{y z}{y + z} = \frac{1}{a^{3}} ， \frac{x z}{x + z} = \frac{1}{a^{3} + b^{3}} ， \frac{x y z}{x y + y z + z x} = \frac{2}{81}$ ，则 $a$ 的值为．

查看试题解析
11. 已知 $x = \sqrt{3} + 1$ ， $y = \sqrt{3} - 1$ ，则代数式 $\frac{y}{x} + \frac{x}{y}$ 的值是．

查看试题解析
12. 如果一个自然数M的个位数字不为0，且能分解成 $A \times B$ （ $A \geq B$ ），其中A与B都是两位数，A与B的十位数字相同，个位数字之和为6，则称数M为“如意数”，并把数M分解成 $M = A \times B$ 的过程，称为“快乐分解”．例如，因为 $528 = 22 \times 24$ ， 22和24的十位数字相同，个位数字之和为6，所以528是“如意数”．

(1)、最小的“如意数”是；

(2)、把一个“如意数”M进行“快乐分解”，即 $M = A \times B$ ， A与B的和记为 $P （ M ）$ ， A与B的差记为 $Q （ M ）$ ，若 $\frac{P (M)}{Q (M)}$ 能被7整除，则M的值为．

查看试题解析
13. 欧拉是18世纪瑞士著名的数学家，他的贡献不仅遍及高等数学的各个领域，在初等数学中也留下了他的足迹．下面是关于分式的欧拉公式：
$\frac{a^{r}}{(a - b) (a - c)} + \frac{b^{r}}{(b - c) (b - a)} + \frac{c^{r}}{(c - a) (c - b)} = {\begin{cases} p ， & r = 0 时 \\ 0 ， & r = 1 时 \\ 1 ， & r = 2 时 \\ a + b + c ， & r = 3 时 \end{cases}$

（其中a，b，c均不为零，且两两互不相等）．

(1)、当 $r = 0$ 时，常数p的值为．

(2)、利用欧拉公式计算： $\frac{202 2^{3}}{2} - 202 1^{3} + \frac{202 0^{3}}{2} =$ ．

查看试题解析
14. 人们把 $\frac{\sqrt{5} - 1}{2} \approx 0.618$ 这个数叫做黄金比，著名数学家华罗庚优选法中的“0.618法”就应用了黄金比.设 $a = \frac{\sqrt{5} - 1}{2}$ ， $b = \frac{\sqrt{5} + 1}{2}$ ，记 $S_{1} = \frac{1}{1 + a} + \frac{1}{1 + b}$ ， $S_{2} = \frac{2}{1 + a^{2}} + \frac{2}{1 + b^{2}}$ ，…， $S_{100} = \frac{100}{1 + a^{100}} + \frac{100}{1 + b^{100}}$ ，则 $S_{1} + S_{2} + \dots + S_{100} =$ .

查看试题解析

三、计算题

15. 先化简，再求值： $(\frac{1}{x - y} - \frac{1}{x + y}) \div \frac{2 x}{x^{2} + 2 x y + y^{2}}$ ，其中 $x = \sqrt{3} - \sqrt{2}$ ， $y = \sqrt{3} + \sqrt{2}$ ．

查看试题解析
16. 已知 $a + b + c = 0$ ，且 $a b c \neq 0$ ，求： $a (\frac{1}{b} + \frac{1}{c}) + b (\frac{1}{a} + \frac{1}{c}) + c (\frac{1}{a} + \frac{1}{b})$ 的值.

查看试题解析

四、实践探究题

17. 阅读下列材料，并解答总题：
材料：将分式 $\frac{x^{2} - x + 3}{x + 1}$ 拆分成一个整式与一个分式（分子为整数）的和的形式．
解：由分母x+1，可设 $x^{2} - x + 3 = (x + 1) (x + a) + b$
则 $x^{2} - x + 3 = (x + 1) (x + a) + b = x^{2} + a x + x + a + b$
= $x^{2} + (a + 1) x + a + b$
∵对于任意 $x$ 上述等式成立
∴ ${\begin{array}{l} a + 1 = - 1 \\ a + b = 3 \end{array}$ ，
解得 ${\begin{array}{l} a = - 2 \\ b = 5 \end{array}$ ，
∴ $\frac{x^{2} - x + 3}{x + 1} = \frac{(x + 1) (x - 2) + 5}{x + 1} = x - 2 + \frac{5}{x + 1}$
这样，分式 $\frac{x^{2} - x + 3}{x + 1}$ 就拆分成一个整式 $(x - 2)$ 与一个分式 $\frac{5}{x + 1}$ 的和的形式．

(1)、将分式 $\frac{x^{2} + 6 x - 3}{x - 1}$ 拆分成一个整式与一个分式（分子为整数）的和的形式为；

(2)、已知整数 $x$ 使分式 $\frac{2 x^{2} + 5 x - 20}{x - 3}$ 的值为整数，则满足条件的整数 $x$ = ．

查看试题解析
18. 阅读理解：
符号 $|\begin{matrix} a & c \\ b & d \end{matrix}| ，$ 称为二阶行列式，规定它的运算法则为 $|\begin{matrix} a & c \\ b & d \end{matrix}| = a d - b c .$ 例如 $|\begin{matrix} 3 & 5 \\ 2 & 4 \end{matrix}| = 3$ ×4-2×5=2.
请根据以上材料，化简下面的二阶行列式：
$|\begin{matrix} \frac{a}{a - 1} & a + 1 \\ \frac{1}{1 - a} & 1 \end{matrix}| .$

查看试题解析
19. 通过小学的学习我们知道，分数可分为“真分数”和“假分数”，而假分数都可化为带分数 $.$ 如： $\frac{8}{3} = \frac{6 + 2}{3} = 2 + \frac{2}{3} = 2 \frac{2}{3} .$ 我们定义：在分式中，对于只含有一个字母的分式，当分子的次数大于或等于分母的次数时，我们称之为“假分式”；当分子的次数小于分母的次数时，我们称之为“真分式”．
如 $\frac{x - 1}{x + 1}$ ， $\frac{x^{2}}{x - 1}$ 这样的分式就是假分式； $\frac{3}{x + 1} ， \frac{2 x}{x^{2} + 1}$ 这样的分式就是真分式 $.$ 类似地，假分式也可以化为带分式 $($ 即：整式与真分式的和的形式 $)$ ．
如： $\frac{x - 1}{x + 1} = \frac{(x + 1) - 2}{x + 1} = 1 - \frac{2}{x + 1}$ ； $\frac{x^{2}}{x - 1} = \frac{x (x - 1) + (x - 1) + 1}{x - 1} = x + 1 + \frac{1}{x - 1}$ ．
解决下列问题：

(1)、分式 $\frac{2024}{x}$ 是分式 $($ 填“真”或“假” $)$ ；

(2)、将假分式 $\frac{x + 3}{x + 2}$ 化为带分式；

(3)、求所有符合条件的整数 $x$ 的值，使得 $\frac{3 x + 7}{x + 1} - \frac{x - 1}{x} \div \frac{x^{2} - 1}{x^{2} + 3 x}$ 的值为整数．

查看试题解析
20. 在分式 $\frac{N}{M}$ 中，若 $M$ ， $N$ 为整式，分母 $M$ 的次数为 $a$ ，分子 $N$ 的次数为 $b$ (当 $N$ 为常数时， $b = 0$ )，则称分式 $\frac{N}{M}$ 为 $a - b$ 次分式．例如， $\frac{1}{x^{4}}$ ， $\frac{x + 1}{x^{5} - 2 x}$ ， $\frac{x^{3}}{x^{7}}$ 均为四次分式.

(1)、在下列分式 $\frac{1}{x^{3}}$ ， $\frac{x + 1}{x^{4}}$ ， $\frac{4 x^{2}}{x^{3} - 2}$ 中，是字母 $x$ 的三次分式的有；

(2)、已知， $A = \frac{m x + 2}{x - 3}$ ， $B = \frac{n x + 3}{x^{2} - 9}$ (其中 $m$ ， $n$ 为常数).
①若 $m = 0$ ， $n = - 4$ ，则 $A + B$ ， $A \cdot B$ ， $A^{2}$ 中，化简后是二次分式的为 ▲ ；
②若 $A$ 与 $B$ 的和化简后是一次分式，且分母的次数为1，求 $3 m - n$ 的值.

查看试题解析
21. 阅读下面材料：
一个含有多个字母的式子中，如果任意交换两个字母的位置，式子的值都不变，这样的式子就叫做对称式，例如： $a + b + c$ ， $a b c$ ， $a^{2} + b^{2}$ ， $\dots$
含有两个字母 $a 、 b$ 的对称式的基本对称式是 $a + b$ 和 $a b$ ，像 $a^{2} + b^{2}$ ， $(a + 2) (b + 2)$ 等对称式都可以用 $a + b$ ， $a b$ 表示，例如： $a^{2} + b^{2} = (a + b)^{2} - 2 a b$ .
请根据以上材料解决下列问题：

(1)、式子：① $a^{2} b^{2}$ ， ② $a^{2} - b^{2}$ ， ③ $\frac{1}{a} + \frac{1}{b}$ ， ④ $a^{2} b - a b^{2}$ 中，属于对称式的是（填序号）；

(2)、已知 $(x + a) (x + b) = x^{2} + m x + n$ .
①用含 $m 、 n$ 的式子表示对称式 $a + b$ ， $a b$ ；
②若 $m^{2} - n^{2} = 0$ ，求对称式 $\frac{a^{2} + 1}{a} + \frac{b^{2} + 1}{b}$ 的最小值.

查看试题解析
22. 嘉嘉和淇淇一起做分式的游戏，如图所示他们面前各有三张牌（互相可以看到对方的牌），两人各自任选两张牌分别做分子和分母，组成一个分式，然后两人均取一个相同的x值，再计算分式的值，值大者为胜．为使分式有意义，他们约定x是大于3的正整数．

(1)、嘉嘉组成的分式中值最大的分式是，淇淇组成的分式中值最大的分式是；

(2)、淇淇说：“虽然我是三张带减号的牌，但最终我一定是胜者”．你同意她的说法吗？通过计算说明．

查看试题解析

【培优卷】2024年北师大版数学八（下）5.3分式的加减法 同步练习

一、选择题

二、填空题

三、计算题

四、实践探究题

【培优卷】2024年北师大版数学八（下）5.3分式的加减法同步练习