湖北省襄阳市保康县2024年中考一模数学试卷
试卷更新日期:2024-04-19 类型:中考模拟
一、选择题(本大题共10个小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的,请将其标号在答题卡上涂黑作答.)
-
1. 下面四个数中比﹣2小的数是( )A、1 B、0 C、﹣1 D、﹣32. 下面的四个交通标志图案中,不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 不等式1﹣x<﹣1的解集在数轴上表示正确的是( )A、
3. 不等式1﹣x<﹣1的解集在数轴上表示正确的是( )A、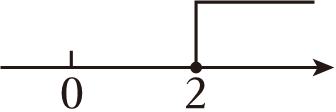 B、
B、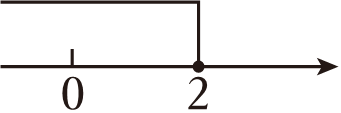 C、
C、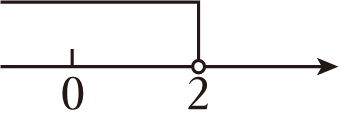 D、
D、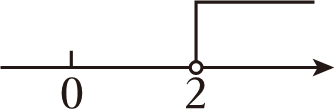 4. 下列计算正确的是( )A、(a2)3=a5 B、a6÷a3=a2 C、 D、5. 将一副三角板按如图所示的方式放置,60°和45°两个角的顶点重合,等腰直角三角板的斜边与另一个三角板的较长直角边平行,且直角顶点在较长直角边上,则图中∠1等于( )
4. 下列计算正确的是( )A、(a2)3=a5 B、a6÷a3=a2 C、 D、5. 将一副三角板按如图所示的方式放置,60°和45°两个角的顶点重合,等腰直角三角板的斜边与另一个三角板的较长直角边平行,且直角顶点在较长直角边上,则图中∠1等于( ) A、45° B、60° C、75° D、90°6. 如图所示,由四个相同的小正方体组成的几何图形的左视图是( )
A、45° B、60° C、75° D、90°6. 如图所示,由四个相同的小正方体组成的几何图形的左视图是( ) A、
A、 B、
B、 C、
C、 D、
D、 7. 下列说法正确的是( )A、对参加中考进入考场考生的安检用随机抽样抽查 B、某次竞赛6人得100分,2人得98分,这8人的平均成绩是99分 C、某种彩票中奖的概率是1%,那么买100张这种彩票一定中奖 D、“射击运动员射击一次,命中靶心”是随机事件8. 如图,厂房屋顶人字架(等腰三角形)的上弦AB=am , ∠B=36°,则跨度BC的长为( )m .
7. 下列说法正确的是( )A、对参加中考进入考场考生的安检用随机抽样抽查 B、某次竞赛6人得100分,2人得98分,这8人的平均成绩是99分 C、某种彩票中奖的概率是1%,那么买100张这种彩票一定中奖 D、“射击运动员射击一次,命中靶心”是随机事件8. 如图,厂房屋顶人字架(等腰三角形)的上弦AB=am , ∠B=36°,则跨度BC的长为( )m . A、2a•sin36° B、2a•cos36° C、 D、9. 如图,点A , B , C , D在⊙O上,OA⊥BC , ∠ADC=25°,则∠CAB的度数是( )
A、2a•sin36° B、2a•cos36° C、 D、9. 如图,点A , B , C , D在⊙O上,OA⊥BC , ∠ADC=25°,则∠CAB的度数是( ) A、140° B、130° C、120° D、110°10. 对称轴是直线x=﹣1的抛物线y=ax2+bx+c(a , b , c为常数,a<0)与x轴相交于(x1 , 0),(x2 , 0)两点,1<x2<2,下列正确的是( )A、﹣3<x1<﹣2 B、4ac﹣b2>0 C、4a﹣2b+c>0 D、3a+c<0
A、140° B、130° C、120° D、110°10. 对称轴是直线x=﹣1的抛物线y=ax2+bx+c(a , b , c为常数,a<0)与x轴相交于(x1 , 0),(x2 , 0)两点,1<x2<2,下列正确的是( )A、﹣3<x1<﹣2 B、4ac﹣b2>0 C、4a﹣2b+c>0 D、3a+c<0二、填空题(本大题共5个小题,每小题3分,共15分.把答案填在答题卡的相应位置上.)
-
11. 式子在实数范围内有意义的条件是 .12. 若反比例函数的图象所在的每一个象限内,y随x的增大而减小,请写出一个符合条件的k的值 .13. 三名同学去打乒乓球,三人决定按下面规则确定哪两个先打.规则:三人同时出单手,出手手势只能用手心或手背,若两人出手心一人出手背,则出手心的两人先打;若两人出手背一人出手心,则出手背的两人先打;若三个都出手心或手背,则重新出手.三人只出手一次就能决定出两人先打的概率是 .14. 《孙子算经》下卷第28题译成现代文意思是:现有甲乙二人,身边各有多少钱,不清楚.如果甲的钱数加上乙的钱数的一半,钱数一共是48;如果乙的钱数加上甲的钱数的 , 钱数一共也是48.问甲乙二人各有多少钱.答:甲的钱数是 , 乙的钱数是 .15. 如图,将一张正方形纸片ABCD折叠,折痕为AE , 折叠后,点B的对应点落在正方形内部的点F处,连接DF并延长交BC于点G . 若BG=CG , AD=2,则EG的长为 .

三、解答题(本大题共9个小题,共75分,解答应写出文字说明、证明过程或演算步骤,并且写在答题卡上每题对应的答题区域内.)
-
16. 计算: .17. 如图,矩形ABCD的对角线AC , BD相交于点O , 且DE∥AC , CE∥BD交于点E . 求证:四边形CEDO是菱形.
 18. 2022年3月25日,教育部印发《义务教育课程方案》和《课程标准(2022年版)》,优化了课程设置,将劳动从综合与实践课程中独立出来.为了体验劳动的快乐,亲历劳动的过程,某班组织学生到菜园进行了蔬菜采摘活动.班主任将该班学生分成甲、乙两组,在相同的采摘时间内,甲组采摘了270千克,乙组采摘了225千克,平均每小时甲组比乙组多采摘30千克,请用列方程的方法求平均每小时甲、乙两个小组各采摘多少千克.19. 每年的4月15日是我国全民国家安全教育日,某中学为了解七年级学生对“国家安全法”知识的掌握情况,对七年级A , B两个班进行了“国家安全法”知识测试,满分10分,测试成绩都为整数,测试成绩不低于9分的为优秀.
18. 2022年3月25日,教育部印发《义务教育课程方案》和《课程标准(2022年版)》,优化了课程设置,将劳动从综合与实践课程中独立出来.为了体验劳动的快乐,亲历劳动的过程,某班组织学生到菜园进行了蔬菜采摘活动.班主任将该班学生分成甲、乙两组,在相同的采摘时间内,甲组采摘了270千克,乙组采摘了225千克,平均每小时甲组比乙组多采摘30千克,请用列方程的方法求平均每小时甲、乙两个小组各采摘多少千克.19. 每年的4月15日是我国全民国家安全教育日,某中学为了解七年级学生对“国家安全法”知识的掌握情况,对七年级A , B两个班进行了“国家安全法”知识测试,满分10分,测试成绩都为整数,测试成绩不低于9分的为优秀.【收集整理数据】测试结果显示所有学生成绩都不低于6分,随机从A , B两个班各抽取m名学生的测试成绩,从抽取成绩来看,A , B两班级得8分的人数相同.
【描述数据】根据抽取的学生成绩,绘制出了如下统计图.

【分析数据】两个班级样本数据的平均数、中位数、众数、方差如表:
年级
平均数
中位数
众数
方差
A班
8.5
8.5
10
2.05
B班
8.5
p
9
1.45
根据以上信息,解答下列问题:
(1)、m= , n= , p=;(2)、补全条形统计图;(3)、A班共有50人参加测试,估计A班测试成绩优秀的有人;(4)、小明的成绩是9分,他的成绩在本班抽取的成绩之中,该班有4个抽取的成绩比他的低,小明在班(填“A”或“B”);(5)、请从众数和方差这两个统计量中任意选一个,对两个班的测试成绩进行评价.20. 如图,一次函数y=mx+n(m , n为常数,m≠0)与反比例函数y=(k为常数,k≠0)的图象相交于A(﹣2,3),B(3,﹣2)两点. (1)、求m , n , k的值;(2)、请直接写出关于x的不等式<mx+n<0的解集.21. AB是⊙O的直径,∠ABT=45°,AT=AB , BT与⊙O相交于点C .
(1)、求m , n , k的值;(2)、请直接写出关于x的不等式<mx+n<0的解集.21. AB是⊙O的直径,∠ABT=45°,AT=AB , BT与⊙O相交于点C . (1)、如图1,求证:AT是⊙O的切线;(2)、如图2,连接AC , 过点O作OD⊥AC分别交AT , AC于点D , E , 交AC于点F , 若 , 求图中阴影部分的面积.22. 随着家用小轿车的普及,交通安全已经成为千家万户关注的焦点,保持安全车距是预防交通事故的关键.某兴趣小组调查了解到某型号汽车紧急刹车后车速每秒减少a(m/s),该型号汽车刹车时速度为v0(m/s),刹车后速度v(m/s)、行驶的距离为s(m)与时间t(s)之间的关系如表:
(1)、如图1,求证:AT是⊙O的切线;(2)、如图2,连接AC , 过点O作OD⊥AC分别交AT , AC于点D , E , 交AC于点F , 若 , 求图中阴影部分的面积.22. 随着家用小轿车的普及,交通安全已经成为千家万户关注的焦点,保持安全车距是预防交通事故的关键.某兴趣小组调查了解到某型号汽车紧急刹车后车速每秒减少a(m/s),该型号汽车刹车时速度为v0(m/s),刹车后速度v(m/s)、行驶的距离为s(m)与时间t(s)之间的关系如表:t
…
1
1.5
2
2.5
…
v
…
15
12.5
10
7.5
…
s
…
17.5
24.375
30
34.375
…
(1)、求v与t的函数关系式;(2)、s与t满足函数关系式s=pt2+qt , 求该汽车刹车后行驶的最大距离;(3)、普通司机在遇到紧急情况时,从发现情况到刹车的反应时间是b(s),0.5≤b≤0.8,一个普通司机驾驶该型汽车以v0(m/s)的速度行驶,突然发现导航提示前面60m处路面变窄,需要将车速降低到5m/s以下安全通过,司机紧急刹车,能否在到达窄路时将车速降低到5m/s以下?请通过计算说明.23. 在△ABC中,AC=BC , 点D是边AB上不与点B重合的一动点,将△BDC绕点D旋转得到△EDF , 点B的对应点E落在直线BC上,EF与AC相交于点G , 连接AF . (1)、如图1,当点D与点A重合时,
(1)、如图1,当点D与点A重合时,①求证:∠C=∠CEF;
②判断AF与BC的位置关系是 ▲ ;
(2)、如图2,当点D不与点A重合,点E在边BC上时,判断AF与BC的位置关系,并写出证明过程;(3)、如图3,当点D是AB的中点,点E在边BC上时,延长BA , CF相交于点P , 若AB=CD=2,求PF的长.24. 在平面直角坐标系中,抛物线y=ax2+bx经过点A(t , 0),与直线y=x+4交于点B(﹣1,3),C(4,8)两点,点P是直线BC下方抛物线上不与O , A重合的一动点,过点P作BC的平行线交x轴于点Q , 设点P的横坐标为m . (1)、请直接写出a , b , t的值;(2)、如图,若抛物线的对称轴为直线l , 点P在直线l的右侧,PQ与直线l交于点M , 当M为PQ的中点时,求m的值;(3)、线段PQ的长记为d .
(1)、请直接写出a , b , t的值;(2)、如图,若抛物线的对称轴为直线l , 点P在直线l的右侧,PQ与直线l交于点M , 当M为PQ的中点时,求m的值;(3)、线段PQ的长记为d .①求d关于m的函数解析式;
②若 , 结合d关于m的函数图象,直接写出m的取值范围.