广东省中山市2024年中考一模数学试卷

试卷更新日期：2024-04-19 类型：中考模拟

进入出卷网下载

一、选择题（共10小题，满分30分，每小题3分）

1. $\frac{1}{3}$ 的相反数是（）

A、 $\frac{1}{3}$ B、 $\pm \frac{1}{3}$ C、-- $\frac{1}{3}$ D、3

查看试题解析
2. 今年是共建“一带一路”倡议提出10周年，也是构建人类命运共同体理念提出10周年.2013年到2022年，中国与“一带一路”共建国家的累计双向投资超过3800亿美元.3800亿用科学记数法表示为（　　）

A、38×10¹⁰ B、3.8×10¹¹ C、0.38×10¹² D、3.8×10¹²

查看试题解析
3. 下列计算正确的是（）

A、x+x＝2x² B、（x²）³＝x⁵ C、（2x）²＝2x² D、x³•x²＝x⁵

查看试题解析
4. 下列各式从左到右的变形，因式分解正确的是（）

A、a（a+b）＝a²+ab B、a²+ab﹣3＝a（a+b）﹣3 C、2ab²﹣8a＝2a（b²﹣4） D、a²﹣2a﹣8＝（a+2）（a﹣4）

查看试题解析
5. 学习组织“超强大脑”答题赛，参赛的11名选手得分情况如表所示，那么这11名选手得分的中位数和众数分别是（）
分数（分）
60
80
90
95
人数（人）
2
2
3
4

A、86.5和90 B、80和90 C、90和95 D、90和90

查看试题解析
6. 若关于x的方程 $\frac{x}{x - 3} - 2 = \frac{m}{x - 3}$ 有正数解，则（）．

A、m＞0且m≠3 B、m＜6且m≠3 C、m＜0 D、m＞6

查看试题解析
7. 如图，量角器外缘上有A ， B ， C三点，它们所对应的读数分别是80°，50°，180°，则∠ACB为（）

A、50° B、30° C、25° D、15°

查看试题解析
8. 如图， $△ A B C$ 的内切圆 $⊙ O$ 与 $B C$ ， $A C$ ， $A B$ 分别相切于点 $D$ ， $E$ ， $F$ ，且 $∠ C = 90 °$ ， $A C = 8$ ， $B C = 6$ ，则阴影部分（即四边形 $C E O D$ ）的面积为（）

A、4 B、6.25 C、7.5 D、9

查看试题解析
9. 在锐角△ABC中，AD⊥BC，BE⊥AC，垂足分别为D、E，AD与BE交于点F，BF＝AC那么∠ABC等于（）

A、60° B、50° C、48° D、45°

查看试题解析
10. 如图，一段抛物线y＝﹣x²+8x（0≤x≤8）记为C₁ ，它与x轴交于点O ， A₁两点；将C₁绕点A₁旋转180°得到C₂ ，交x轴于点A₂；将C₂绕点A₂旋转180°得到C₃ ，交x轴于点A₃ ， …，如此下去，得到一条“波浪线”．若点M（2023，m）在此“波浪线”上，则m的值为（）

A、﹣8 B、8 C、﹣7 D、7

查看试题解析

二、填空题（共5小题，满分20分，每小题4分）

11. 使二次根式 $\sqrt{3 x - 1}$ 有意义的条件是．

查看试题解析
12. 若将A（2，b）向下平移4个单位得B ，且A与B关于x轴对称，则b＝．

查看试题解析
13. 如图，△AOB与△COD是位似图形，且OA＝AC ，则△AOB与△COD的相似比为．

查看试题解析
14. 关于x的一元二次方程2x²+4mx+m=0有两个不同的实数根x₁ ， x₂ ，且 $x_{1}^{2} + x_{2}^{2} = \frac{3}{16}$ ，则m= ．

查看试题解析
15. 如图，在△ABC中，∠ABC＝60°，AB＝4，AC＝2 $\sqrt{7}$ ，则BC＝；若点D是边AC上的动点（不与点A ， C重合），将线段BD绕点B逆时针旋转60°得到线段BE ，连接AE ，当线段AE取最小值时，则CD＝．

查看试题解析

三、解答题（共9小题，满分70分）

16. 计算：（π﹣2022）⁰﹣3tan30°+|1﹣ $\sqrt{3}$ |+ $(\frac{1}{2})$ ^﹣2 ．

查看试题解析
17. 先化简，再求值： $(\frac{1}{a} + \frac{1}{a + 1}) \div \frac{4 a^{2} - 1}{a^{2} + a}$ ，其中a＝ $\frac{\sqrt{3} + 1}{2}$ ．

查看试题解析
18. 又到一年丰收季，重庆外国语学校“国内中考、高考、国内保送、出国留学”捷报频传．作为准初三的初二年级学生希望抓紧暑期更好的提升自我．张同学采用随机抽样的方式对初二年级学生此次暑期生活的主要计划进行了问卷调查，并将调查结果按照“A社会实践类、B学习提高类、C游艺娱乐类、D其他”进行了分类统计，并绘制了如图1和如图2两幅不完整的统计图．（接受调查的每名同学只能在四类中选择其中一种类型，不可多选或不选．）请根据图中提供的信息完成以下问题．

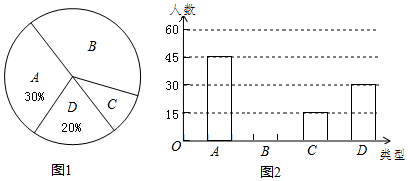(1)、扇形统计图中表示B类的扇形的圆心角是度，并补全条形统计图；

(2)、张同学已从被调查的同学中确定了甲、乙、丙、丁四名同学进行开学后的经验交流，并计划在这四人中选出两人的宝贵经验刊登在本班班刊上．请利用画树状图或列表的方法求出甲同学的经验刊登在班刊上的概率．

查看试题解析
19. 2022年我国已成为全球最大的电动汽车市场，电动汽车在保障能源安全，改善空气质量等方面较传统汽车都有明显优势．经过对某款电动汽车和某款燃油车的对比调查发现，电动汽车平均每公里的充电费比燃油车平均每公里的加油费少0.6元．若充电费和加油费均为300元时，电动汽车可行驶的总路程是燃油车的4倍，求这款电动汽车平均每公里的充电费．

查看试题解析
20. 为了解决中低收入困难家庭的住房问题，某县新增了如图所示的甲、乙两幢保障性住房，线段AB、DC分别表示甲、乙两幢保障性住房的高，AB⊥BC ， DC⊥BC ，从B点测得D点的仰角α为60°，从A点测得D点的仰角β为30°，已知甲幢保障性住房高AB＝36米．

(1)、求乙幢保障性住房的高DC；

(2)、求甲、乙两幢保障性住房之间的距离BC（结果精确到0.01米）．
（参考数据： $\sqrt{2}$ ≈1.414， $\sqrt{3}$ ≈1.732）

查看试题解析
21. 某商家销售某种商品，每件进价为40元．经市场调查发现，该商品一周的销售量y（大于0的整数）件与销售单价x（不低于50的整数）满足一次函数关系，部分调查数据如表：
销售单价x（元/件）
50
55
60
70
75
…
一周的销售量y（件）
500
450
400
300
250
…

(1)、直接写出销售量y关于销售单价x的函数表达式：y＝．

(2)、若一周的销售利润为2750元，则销售单价是多少元/件？

(3)、现商家决定将商品一周的销售利润作为捐款寄往贫困地区，则捐款能达到的最大值是元．

查看试题解析
22. 如图，点A，B，C在圆O上， $∠ A B C = 60 °$ ，直线 $A D ∥ B C$ ， $A D = A B$ ，点O在 $B D$ 上．

(1)、求证 $A D$ 是圆O的切线

(2)、若 $B C = 6 \sqrt{3}$ ，求圆O的半径．

查看试题解析
23. 已知： $y = a x^{2} + \frac{10}{3} \sqrt{3} x + c$ 与x轴交于A、B两点，与y的轴交点C（0，3），对称轴为直线 $x = \frac{5}{3} \sqrt{3}$ ．

(1)、如图1，求抛物线的解析式；

(2)、如图2，点D在抛物线上，连接CD ，且∠OCD＝120°，过D作DG⊥OB于点G ，连接CG ，试判断△CGD的形状，并说明理由；

(3)、如图3，在（2）的条件下，点P在抛物线上，点Q在PD延长线上，FG＝GQ ， CD∥GQ ，在线段CF上取点M ， MG交CQ于N ，当CM＝DE ， CN：NQ＝1：2时，求P点坐标．

查看试题解析
24. 我们定义：对角线互相垂直且相等的四边形叫做“神奇四边形”．

(1)、在我们学过的下列四边形①平行四边形②矩形③菱形④正方形中，是“神奇四边形”的是（填序号）；

(2)、如图1，在正方形ABCD中，E为BC上一点，连接AE ，过点B作BG⊥AE于点H ，交CD于点G ，连AG、EG ．
①求证：四边形ABEG是“神奇四边形”；
②如图2，点M、N、P、Q分别是AB、AG、GE、EB的中点．试判断四边形MNPQ是不是“神奇四边形”；

(3)、如图3，点F、R分别在正方形ABCD的边AB、CD上，把正方形沿直线FR翻折，使得BC的对应边B'C'恰好经过点A ，过点A作AO⊥FR于点O ，若AB'＝2，正方形的边长为6，求线段OF的长．

查看试题解析

销售单价x（元/件）	50	55	60	70	75	…
一周的销售量y（件）	500	450	400	300	250	…

分数（分）	60	80	90	95
人数（人）	2	2	3	4