广东省揭阳市揭东区白塔镇2024年中考一模数学试卷
试卷更新日期:2024-04-19 类型:中考模拟
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
-
1. 在同一时刻的阳光下,小明的影子比小强的影子长,那么在同一路灯下( )
A、小明的影子比小强的影子长 B、小明的影子比小强的影子短 C、小明的影子和小强的影子一样长 D、无法判断谁的影子长2. 若点 , , 都在反比例函数的图象上,则、、的大小关系是( )A、 B、 C、 D、3. 抛物线是由抛物线经过某种平移得到,则这个平移可以表述为( )A、向左平移个单位 B、向左平移个单位 C、向右平移个单位 D、向右平移个单位4. 如图,点在上, , 则( )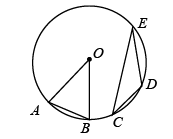 A、48° B、24° C、22° D、21°5. 在中, , , , 则的值为( )A、 B、 C、 D、6. 如图,正方形中,为的中点,于点 , 则等于( )
A、48° B、24° C、22° D、21°5. 在中, , , , 则的值为( )A、 B、 C、 D、6. 如图,正方形中,为的中点,于点 , 则等于( ) A、 B、 C、 D、7. 如图,点在双曲线上,点在双曲线上,轴,点是轴上一点,连接、 , 若的面积是 , 则的值( )
A、 B、 C、 D、7. 如图,点在双曲线上,点在双曲线上,轴,点是轴上一点,连接、 , 若的面积是 , 则的值( ) A、 B、 C、 D、8. 关于的一元二次方程的解为( )A、 , B、 , C、 , D、 ,9. 如图,在直角坐标系中,点在第一象限内,点在轴正半轴上,以点为位似中心,在第三象限内作与的位似比为的位似图形若点的坐标为 , 则点的坐标为( )
A、 B、 C、 D、8. 关于的一元二次方程的解为( )A、 , B、 , C、 , D、 ,9. 如图,在直角坐标系中,点在第一象限内,点在轴正半轴上,以点为位似中心,在第三象限内作与的位似比为的位似图形若点的坐标为 , 则点的坐标为( ) A、 B、 C、 D、10. 已知二次函数 的图象如图所示,有下列5个结论:① ;② ;③ ;④ ( );⑤若方程 =1有四个根,则这四个根的和为2,其中正确的结论有( )
A、 B、 C、 D、10. 已知二次函数 的图象如图所示,有下列5个结论:① ;② ;③ ;④ ( );⑤若方程 =1有四个根,则这四个根的和为2,其中正确的结论有( )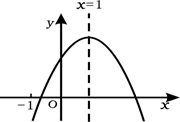 A、2个 B、3个 C、4个 D、5个
A、2个 B、3个 C、4个 D、5个二、填空题:本题共6小题,每小题3分,共18分。
-
11. 若关于 的一元二次方程 有两个相等的实数根,则 的值为 .12. 已知反比例函数是常数,的图象有一支在第二象限,那么的取值范围是 .13. 甲、乙、丙三人站成一排合影留念,则甲、乙二人相邻的概率是 .
14. 如图,在矩形 中, 是 边上一点, 是 边的中点, ,则 .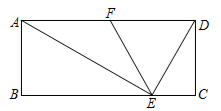 15. 如图,∠AOB是放置在正方形网格中的一个角,则cos∠AOB的值是 .
15. 如图,∠AOB是放置在正方形网格中的一个角,则cos∠AOB的值是 . 16. 如图,在中, , 则下列结论中:;;; , 正确的是填序号 .
16. 如图,在中, , 则下列结论中:;;; , 正确的是填序号 .
三、解答题:本题共9小题,共72分。解答应写出文字说明,证明过程或演算步骤。
-
17. 计算:18. 四边形是菱形,对角线与相交于 , , , 求的长.
 19. 如图,与中, , , 求证:∽ .
19. 如图,与中, , , 求证:∽ . 20. 抛物线顶点坐标是且经过点 .(1)、求该抛物线的解析式;(2)、求该抛物线与坐标轴的交点坐标.21. 如图,是的弦,半径 , 垂足为 , 点在上,连接 , , .
20. 抛物线顶点坐标是且经过点 .(1)、求该抛物线的解析式;(2)、求该抛物线与坐标轴的交点坐标.21. 如图,是的弦,半径 , 垂足为 , 点在上,连接 , , . (1)、若 , 求的度数;(2)、若 , , 求的半径长.22. 有一个抛物线形的拱形桥洞,桥洞离水面的最大高度为 , 跨度为 , 如图所示,把它的图形放在直角坐标系中.
(1)、若 , 求的度数;(2)、若 , , 求的半径长.22. 有一个抛物线形的拱形桥洞,桥洞离水面的最大高度为 , 跨度为 , 如图所示,把它的图形放在直角坐标系中. (1)、求这条抛物线所对应的函数关系式.(2)、如图,在对称轴右边处,桥洞离水面的高是多少?23. 在“文博会”期间,某公司展销如图所示的长方形工艺品,该工艺品长60cm,宽40cm,中间镶有宽度相同的三条丝绸花边.
(1)、求这条抛物线所对应的函数关系式.(2)、如图,在对称轴右边处,桥洞离水面的高是多少?23. 在“文博会”期间,某公司展销如图所示的长方形工艺品,该工艺品长60cm,宽40cm,中间镶有宽度相同的三条丝绸花边.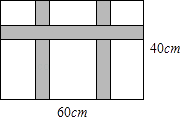 (1)、若丝绸花边的面积为650cm2 , 求丝绸花边的宽度;(2)、已知该工艺品的成本是40元/件,如果以单价100元/件销售,那么每天可售出200件,另每天所需支付的各种费用2000元,根据销售经验,如果将销售单价降低1元,每天可多售出20件,同时,为了完成销售任务,该公司每天至少要销售800件,那么该公司应该把销售单价定为多少元,才能使每天所获销售利润最大?最大利润是多少?24. 如图,AB是⊙O的直径,点D是⊙O外一点,AB=AD,BD交⊙O于点C,AD交⊙O于点E,点P是AC的延长线上一点,连接PB、PD,且PD⊥AD
(1)、若丝绸花边的面积为650cm2 , 求丝绸花边的宽度;(2)、已知该工艺品的成本是40元/件,如果以单价100元/件销售,那么每天可售出200件,另每天所需支付的各种费用2000元,根据销售经验,如果将销售单价降低1元,每天可多售出20件,同时,为了完成销售任务,该公司每天至少要销售800件,那么该公司应该把销售单价定为多少元,才能使每天所获销售利润最大?最大利润是多少?24. 如图,AB是⊙O的直径,点D是⊙O外一点,AB=AD,BD交⊙O于点C,AD交⊙O于点E,点P是AC的延长线上一点,连接PB、PD,且PD⊥AD (1)、判断PB与⊙O的位置关系,并说明理由;(2)、连接CE,若CE=3,AE=7,求⊙O的半径.25. 如图,的两直角边、分别在轴的负半轴和轴的正半轴上,为坐标原点,、两点的坐标分别为、 , 抛物线经过点,且顶点在直线上.
(1)、判断PB与⊙O的位置关系,并说明理由;(2)、连接CE,若CE=3,AE=7,求⊙O的半径.25. 如图,的两直角边、分别在轴的负半轴和轴的正半轴上,为坐标原点,、两点的坐标分别为、 , 抛物线经过点,且顶点在直线上. (1)、求抛物线对应的函数关系式;(2)、若是由沿轴向右平移得到的,当四边形是菱形时,试判断点和点是否在该抛物线上,并说明理由;(3)、在的前提下,若点是所在直线下方该抛物线上的一个动点,过点作平行于轴交于点设点的横坐标为 , 的长度为求与之间的函数关系式,并求取最大值时,点的坐标.
(1)、求抛物线对应的函数关系式;(2)、若是由沿轴向右平移得到的,当四边形是菱形时,试判断点和点是否在该抛物线上,并说明理由;(3)、在的前提下,若点是所在直线下方该抛物线上的一个动点,过点作平行于轴交于点设点的横坐标为 , 的长度为求与之间的函数关系式,并求取最大值时,点的坐标.