浙江省杭州市西湖区十三中教育集团（总校）2023-2024学年九年级下学期数学4月月考试卷

试卷更新日期：2024-04-19 类型：月考试卷

进入出卷网下载

一、选择题(共10小题,每小题3分,共30分)

1. 浙江省博物馆之江馆区，是首批被确定的国家一级博物馆和中央地方共建国家级博物馆，建筑面积逾10万平方米.其中数据10万用科学记数法可表示为（）

A、 $1 \times 1 0^{4}$ B、 $1 \times 1 0^{5}$ C、 $10 \times 1 0^{4}$ D、 $0.1 \times 1 0^{6}$

查看试题解析
2. 如图，现将一块含有60°角的三角板的顶点放在直尺的一边上，若∠2=50°，那么∠1的度数为（）

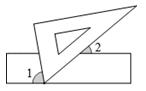A、50° B、60° C、70° D、80°

查看试题解析
3. 下列各式计算正确的是（）

A、 $(- 3 x^{3})^{2} = 9 x^{5}$ B、 $(- 2 a)^{2} = - 4 a^{2}$ C、 $a^{2} \cdot a^{2} = a^{4}$ D、 $(a b^{2})^{3} = a b^{6}$

查看试题解析
4. 在平面直角坐标系中，若点P的坐标为 $(2 ， 1)$ ，则点P关于y轴对称的点的坐标为（）

A、 $(- 2 ， - 1)$ B、 $(2 ， - 1)$ C、 $(1 ， 2)$ D、 $(- 2 ， 1)$

查看试题解析
5. 如图，在平面直角坐标系 $x O y$ 中，有三点 $A (0 ， 1) ， B (4 ， 1) ， C (5 ， 6)$ ，则 $c o s ∠ B A C =$ （）

A、 $\frac{1}{2}$ B、 $\frac{\sqrt{13}}{5}$ C、 $\frac{\sqrt{2}}{2}$ D、 $\frac{\sqrt{3}}{2}$

查看试题解析
6. 在一次800米的长跑比赛中，甲、乙两人所跑的路程 $s$ （米）与各自所用时间 $t$ （秒）之间的函数图象分别为线段 $O A$ 和折线 $O B C D$ ，则下列说法不正确的是（）

A、甲的速度保持不变 B、乙的平均速度比甲的平均速度大 C、在起跑后第180秒时，两人不相遇 D、在起跑后第50秒时，乙在甲的前面

查看试题解析
7. 如图，四边形 $A B C D$ 内接于 $⊙ O$ ，连结 $B D$ ， $O B$ ，若 $∠ A = 7 0^{∘}$ ， $B C = \sqrt{2} O B,$ 则 $∠ D B C$ 的度数为（）

A、 $25 °$ B、 $35 °$ C、 $45 °$ D、 $50 °$

查看试题解析
8. 如图，在矩形ABCD中， $A B = 2 \sqrt{3}$ ， BC＝4，以点D为圆心，DA的长为半径画弧，交BC于点E，交DC的延长线于点F，则图中阴影部分的面积为（）

A、 $\frac{4 π}{3} - 4 \sqrt{3}$ B、 $\frac{4 π}{3} - 2 \sqrt{3}$ C、 $\frac{2 π}{3} - \sqrt{3}$ D、 $\frac{2 π}{3} - 2 \sqrt{3}$

查看试题解析
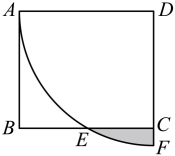9. 已知二次函数 $y = - x^{2} + m^{2} x$ 和 $y = x^{2} - m^{2}$ （m是常数）的图象与x轴都有两个交点，且这四个交点中每相邻两点间的距离都相等，则这两个函数图象对称轴之间的距离为（）

A、2 B、 $m^{2}$ C、4 D、 $2 m^{2}$

查看试题解析
10. 如图，在 $R t △ A B C$ 中， $∠ A B C = 90 °$ ，分别以 $A B$ 、 $A C$ 为边向外作正方形 $A B D E$ 、 $A C F G$ ，连结 $D A$ 并延长交 $F G$ 于点H ，连结 $C H$ ．若 $t a n ∠ H C F = k (0 < k < 1)$ ，则 $\frac{A B}{B C}$ 的值为（）

A、 $\frac{1 - k}{1 + k}$ B、 $\frac{\sqrt{1 - k^{2}}}{1 + k}$ C、 $\frac{k}{1 + k^{2}}$ D、 $\frac{k}{2 - k}$

查看试题解析

二、填空题(共6小题，每小题3分，共18分)

11. 分解因式： $x^{2} - 4 =$

查看试题解析
12. 从 $π$ ， 0， $\frac{13}{7}$ ， 3这四个数中任取一个数，取到无理数的概率是．

查看试题解析
13. 我们定义一种运算程序：已知a ， b ， c均为实数且互不相等， ${[a ， b ， c]}_{m i n}$ 表示三个数中的最小值，若 ${[- 3 t + 2 ， t - 1 ， - 1]}_{m i n}$ 的结果为 $- 1$ ，则t的取值范围是.

查看试题解析
14. 如图1是我国明末《崇祯历书》之《割圆勾股八线表》中所绘的割圆八线图．如图2，根据割圆八线图，在扇形 $A O B$ 中， $∠ A O B = 90 °$ ， $A C$ 和 $B E$ 都是 $⊙ O$ 的切线，点 $A$ 和点 $B$ 是切点， $B E$ 交 $O C$ 于点 $E$ ， $O C$ 交 $⊙ O$ 于点 $D$ ， $A D = C D$ ．若 $O A = 3$ ，则 $C E$ 的长为.

查看试题解析
15. 如图， $A (4 ， 3)$ 是反比例函数 $y = \frac{k}{x}$ 在第一象限图象上一点，连接 $O A$ ，过 $A$ 作 $A B ∥ x$ 轴，截取 $A B = O A$ （ $B$ 在 $A$ 右侧），连接 $O B$ ，交反比例函数 $y = \frac{k}{x}$ 的图象于点 $P$ ．则 $△ O A P$ 的面积为．

查看试题解析
16. 在 $▱ A B C D$ 中，对角线交于点O ， E是 $C D$ 上一点，且 $A O = D E$ ，连结 $A E$ ，当 $∠ B C D - ∠ D A E = 90 °$ 时，若 $∠ O A D = ∠ E D A .$ 则 $∠ A B C =$ °，若 $∠ E D O = 2 ∠ C A E$ ，则 $E D ∶ C E =$ .

查看试题解析

三、解答题(本题8个大题，共72分)

17.

(1)、计算： $\sqrt{32} + {(3.14 - π)}^{0} + | 1 - \sqrt{2} |$ ；

(2)、已知 $\frac{x - 2 y}{x + y} = \frac{2}{5},$ 求 $\frac{x}{y}$ 的值.

查看试题解析
18. 如图的网格中， $△ A B C$ 的顶点都在格点上，每个小正方形的边长均为1．仅用无刻度的直尺在给定的网格图中分别按下列要求画图．（保留画图痕迹，画图过程中辅助线用虚线，画图结果用实线、实心点表示）

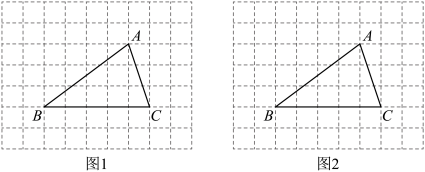(1)、请在图1中画出 $△ A B C$ 的高 $B D$ ．

(2)、请在图2中在线段 $A B$ 上找一点E，使 $A E = 3$ ．

查看试题解析
19. 我校为加强学生安全意识，组织全校学生参加安全知识竞赛．从中抽取部分学生成绩进行统计，绘制以下两幅不完整的统计图．
请根据图中的信息，解决下列问题：

(1)、填空： $a =$ ， $n =$ ；

(2)、补全频数直方图；

(3)、我校共有3000名学生，若成绩在70分以下（含70分）的学生安全意识不强，则我校安全意识不强的学生约有多少人？

查看试题解析
20. 正方形 $A B C D$ 中，点 $E$ 在边 $A D$ 上（不与点 $A$ ， $D$ 重合），射线 $B E$ 与射线 $C D$ 交于点 $F$ ，若 $A E \cdot C F = 9$ ．

(1)、求正方形 $A B C D$ 的边长.

(2)、以点 $B$ 为圆心， $B C$ 长为半径画弧，交线段 $B E$ 于点 $G$ ．若 $E D = 2 E G$ ，求 $E D$ 的长．

查看试题解析
21. 如图，一次函数 $y = a x + b$ 的图象与反比例函数 $y = \frac{k}{x}$ 的图象交于 $A (- 1 ， - 3) ， B (3 ， n)$ 两点．

(1)、求这两个函数的解析式；

(2)、点 $C (0 ， m)$ 为y轴上一个动点，过图中所标的C点作垂直于y轴的直线，分别交反比例函数及一次函数的图象于D ， E两点，当点E位于点D右方时，请直接写出m的取值范围．

查看试题解析
22. 如图， $△ A B C$ 中， $A B = B C$ ，以 $A C$ 为直径的 $⊙ O$ 分别交边 $A B ， B C$ 于点 $D ， E$ ，过点 $A$ 作 $⊙ O$ 的切线交 $C B$ 的延长线于点 $F$ ．

(1)、求证： $A B = B F$ ；

(2)、若 $A F = 8$ ， $c o s ∠ B A F = \frac{4}{5}$ ，求 $B C$ 和 $D E$ 的长．

查看试题解析
23. 如图，灌溉车为绿化带浇水，喷水口 $H$ 离地竖直高度 $O H$ 为 $1.5 m$ ．可以把灌溉车喷出水的上、下边缘抽象为平面直角坐标系中两条抛物线的部分图象；把绿化带横截面抽象为矩形 $D E F G$ ，其水平宽度 $D E = 3 m$ ，竖直高度 $E F = 0.5 m$ ．下边缘抛物线是由上边缘抛物线向左平移得到，上边抛物线最高点 $A$ 离喷水口的水平距离为 $2 m$ 、高出喷水口 $0.5 m$ ，灌溉车到绿化带的距离 $O D$ 为 $d$ （单位： $m$ ）

(1)、求上边缘抛物线的函数解析式，并求喷出水的最大射程 $O C$ ；

(2)、求下边缘抛物线与x轴的正半轴交点 $B$ 的坐标；

(3)、要使灌溉车行驶时喷出的水能浇灌到整个绿化带，直接写出 $d$ 的取值范围

查看试题解析
24. 已知：如图， $△ A B C$ 是锐角三角形，⊙O是以 $A B$ 为直径的圆，交 $B C$ 边于D ， $A C$ 边于E.连结 $A D ， B E$ 交于点F ，若 $B F = A C$

(1)、求证： $A D = B D$ .

(2)、连接 $D E$ ，若 $\frac{D E}{D C} = \frac{\sqrt{6}}{2}$ ，求 $c o s C .$

(3)、若 $A E = A G$ ，连结 $B G$ ，作 $F H ⊥ B G$ 于H点，交 $B A$ 于M点，求证： $\frac{B A}{A M} = \frac{B F}{F M} .$

查看试题解析