浙江省杭州市锦绣育才教育集团2024年中考二模数学试卷
试卷更新日期:2024-04-19 类型:中考模拟
一、选择题(本题有10个小题,每小题3分,共30分.在每小题给出的四个选项中只有一项是最符合题目要求的)
-
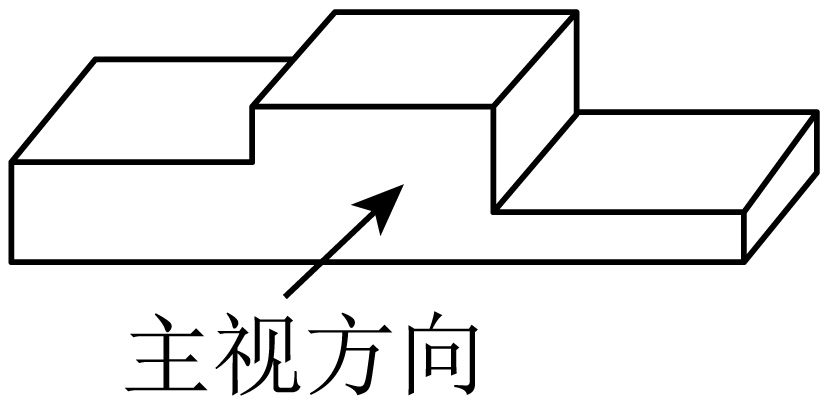
1. 神舟十七号成功发射,太空空间站距离地球约为423000m,423000用科学记数法可表示为( )A、 B、 C、 D、2. 下列运算正确的是( )A、 B、 C、 D、3. 全运会颁奖台如图所示,它的主视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 4. 在一个不透明的袋子装有4个红球,8个白球,它们除颜色外完全相同,从袋中任意摸出一个球为白球的概率为( )A、 B、 C、 D、5. 分式的值,可以等于( )A、 B、0 C、1 D、26. 若点在平面直角坐标系的第二象限内,则x的取值范围在数轴上可表示为( )A、
4. 在一个不透明的袋子装有4个红球,8个白球,它们除颜色外完全相同,从袋中任意摸出一个球为白球的概率为( )A、 B、 C、 D、5. 分式的值,可以等于( )A、 B、0 C、1 D、26. 若点在平面直角坐标系的第二象限内,则x的取值范围在数轴上可表示为( )A、 B、
B、 C、
C、 D、
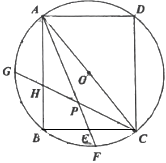
D、 7. 如图,四边形内接于 . 若 , 则的度数为( )
7. 如图,四边形内接于 . 若 , 则的度数为( ) A、 B、 C、 D、8. 二次函数的图象经过两点,若 , 则h的值可能为( )A、3 B、4 C、5 D、69. 某数学小组在研究了函数y1=x与y2= 性质的基础上,进一步探究函数y=y1+y2的性质,经过讨论得到以下几个结论:①函数y=y1+y2的图象与直线y=3没有交点;②函数y=y1+y2的图象与直线y=a只有一个交点,则a=±4;③点(a,b)在函数y=y1+y2的图象上,则点(-a,-b)也在函数y=y1+y2的图象上.以上结论正确的是( )A、①② B、①②③ C、②③ D、①③10. 如图,已知正方形和正方形 , 且A、B、E三点在一条直线上,连接 , 以为边构造正方形交于点M , 连接 , 设 . 若点Q、B、F三点共线, , 则n的值为( )
A、 B、 C、 D、8. 二次函数的图象经过两点,若 , 则h的值可能为( )A、3 B、4 C、5 D、69. 某数学小组在研究了函数y1=x与y2= 性质的基础上,进一步探究函数y=y1+y2的性质,经过讨论得到以下几个结论:①函数y=y1+y2的图象与直线y=3没有交点;②函数y=y1+y2的图象与直线y=a只有一个交点,则a=±4;③点(a,b)在函数y=y1+y2的图象上,则点(-a,-b)也在函数y=y1+y2的图象上.以上结论正确的是( )A、①② B、①②③ C、②③ D、①③10. 如图,已知正方形和正方形 , 且A、B、E三点在一条直线上,连接 , 以为边构造正方形交于点M , 连接 , 设 . 若点Q、B、F三点共线, , 则n的值为( )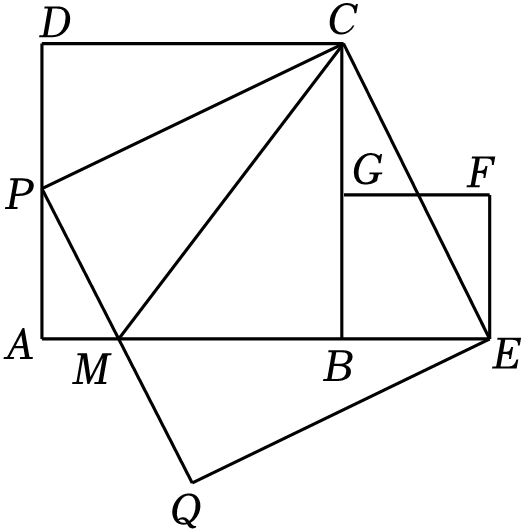 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本题有6个小题,每小题4分,共24分)
-
11. 因式分解: .12. 计算: .13. 如图,将沿对角线折叠,使点B落在点处,若 , 则 .
 14. 图1是一个地铁站人口的双翼闸机.如图2,它的双翼展开时,双翼边缘的端点A与B之间的距离为12cm,双翼的边缘 , 且与闸机侧立面夹角 . 当双翼收起时,可以通过闸机的物体的最大宽度为 .
14. 图1是一个地铁站人口的双翼闸机.如图2,它的双翼展开时,双翼边缘的端点A与B之间的距离为12cm,双翼的边缘 , 且与闸机侧立面夹角 . 当双翼收起时,可以通过闸机的物体的最大宽度为 .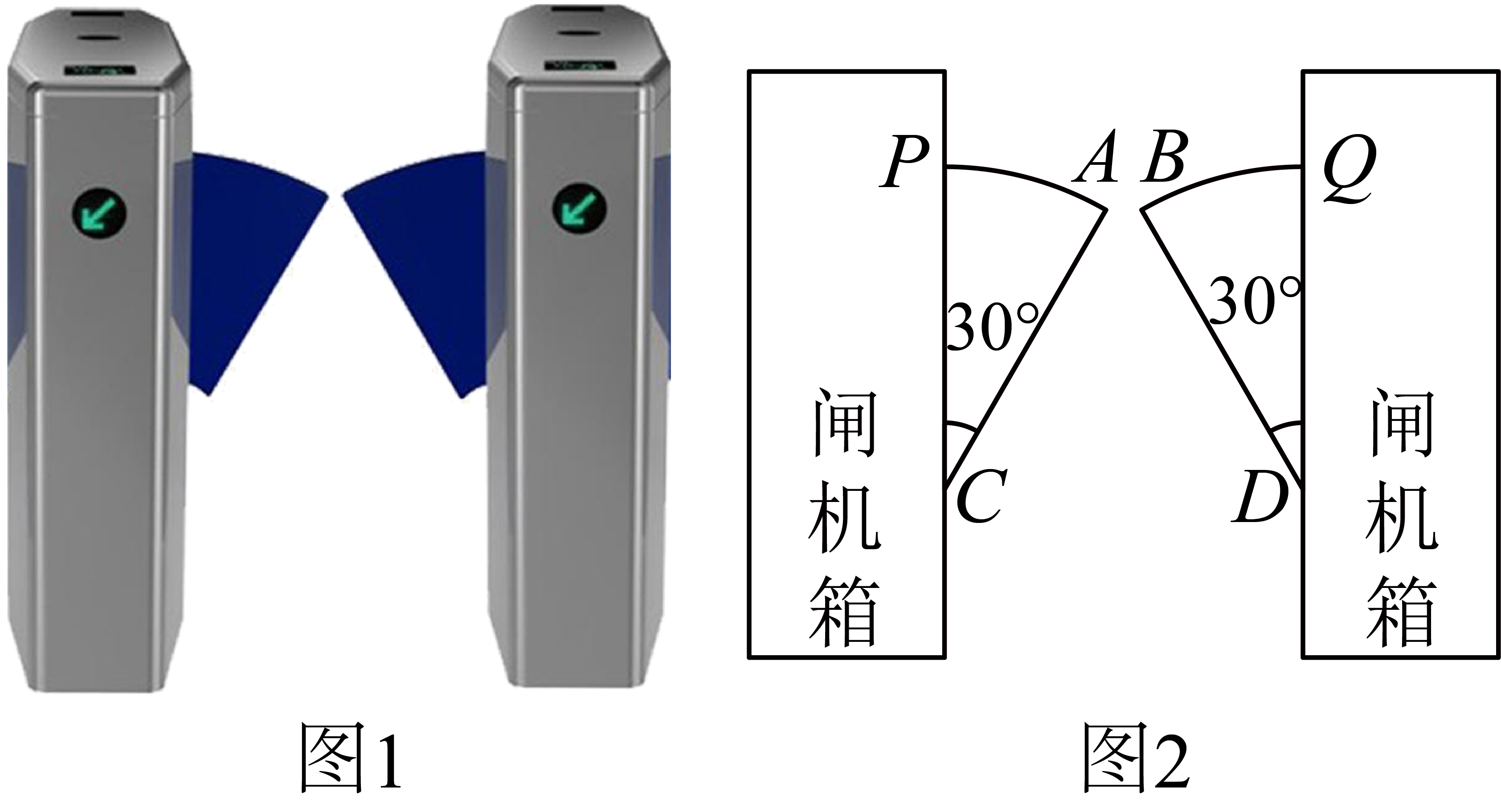 15. 如图,矩形的顶点D在反比例函数的图象上,顶点B , C在x轴上,对角线的延长线交y轴于点E , 连接 , 若的面积是2,则k的值为 .
15. 如图,矩形的顶点D在反比例函数的图象上,顶点B , C在x轴上,对角线的延长线交y轴于点E , 连接 , 若的面积是2,则k的值为 . 16. 如图1,是的直径,E是的中点, , 过点E作交于C、D两点.
16. 如图1,是的直径,E是的中点, , 过点E作交于C、D两点.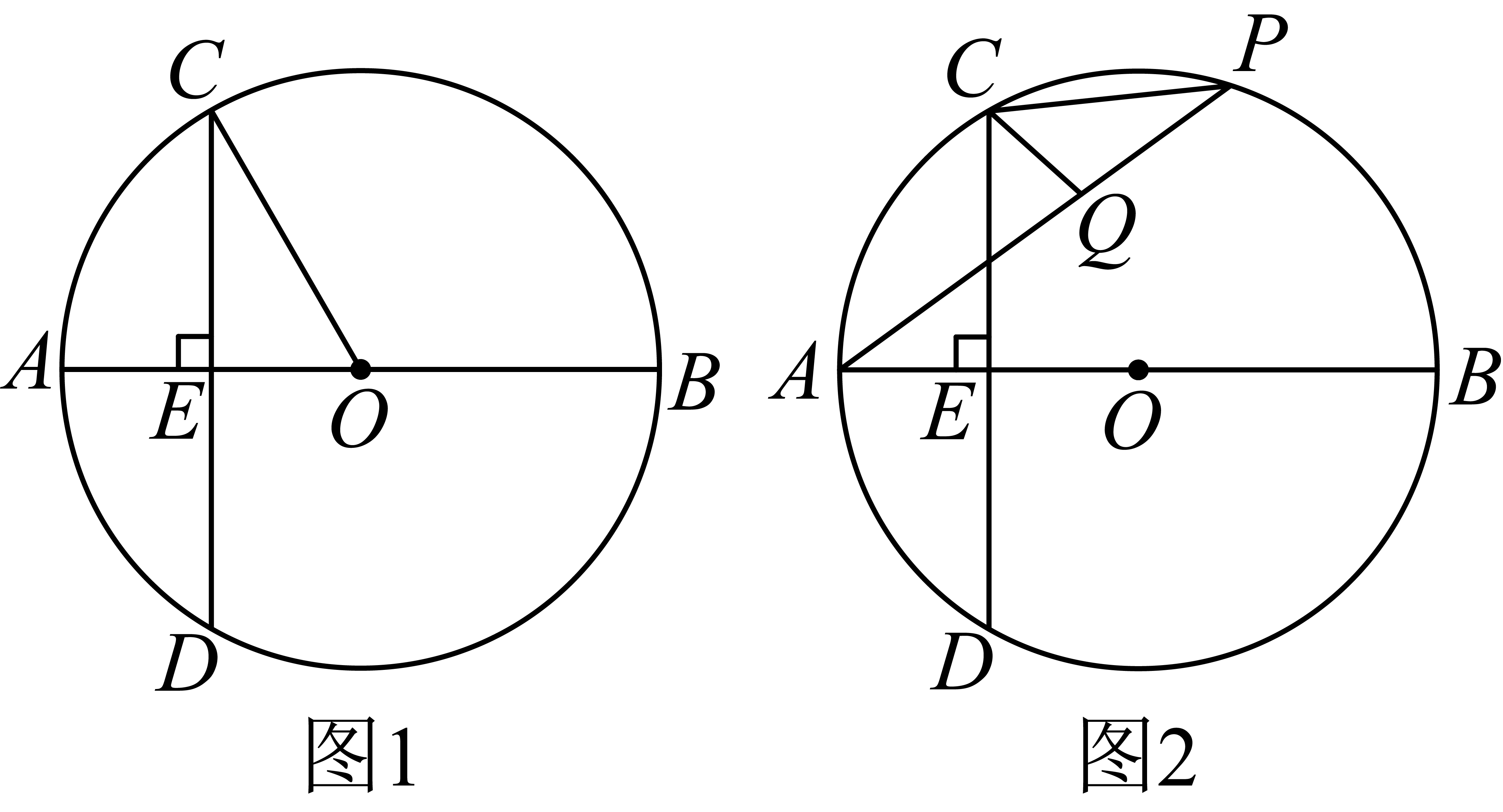 (1)、的度数为;(2)、如图2,P点为劣弧上一个动点(不与B、C重合),连接 , 点Q在上,若时,平分 , 则x的值为 .
(1)、的度数为;(2)、如图2,P点为劣弧上一个动点(不与B、C重合),连接 , 点Q在上,若时,平分 , 则x的值为 .三、解答题(本题有8个小题,共66分,解答应写出文字说明、证明过程或演算步骤)
-
17. 圆圆和方方在做一道练习题:已知 , 试比较与的大小.
圆圆说:“当时,有 , ;因为 , 所以”.
方方说:“圆圆的做法不正确,因为只是一个特例,不具一般性.可以……”请你将方方的做法补充完整.
18. 2024年3月22日是第32届世界水日,为了解同学们对节约和保护水资源知识的掌握情况,学校开展了节约和保护水资源的知识竞赛,从全校1200名学生中随机抽取部分学生的竞赛成绩进行调查分析,并将成绩(满分:100分)制成如图所示的扇形统计图和条形统计图.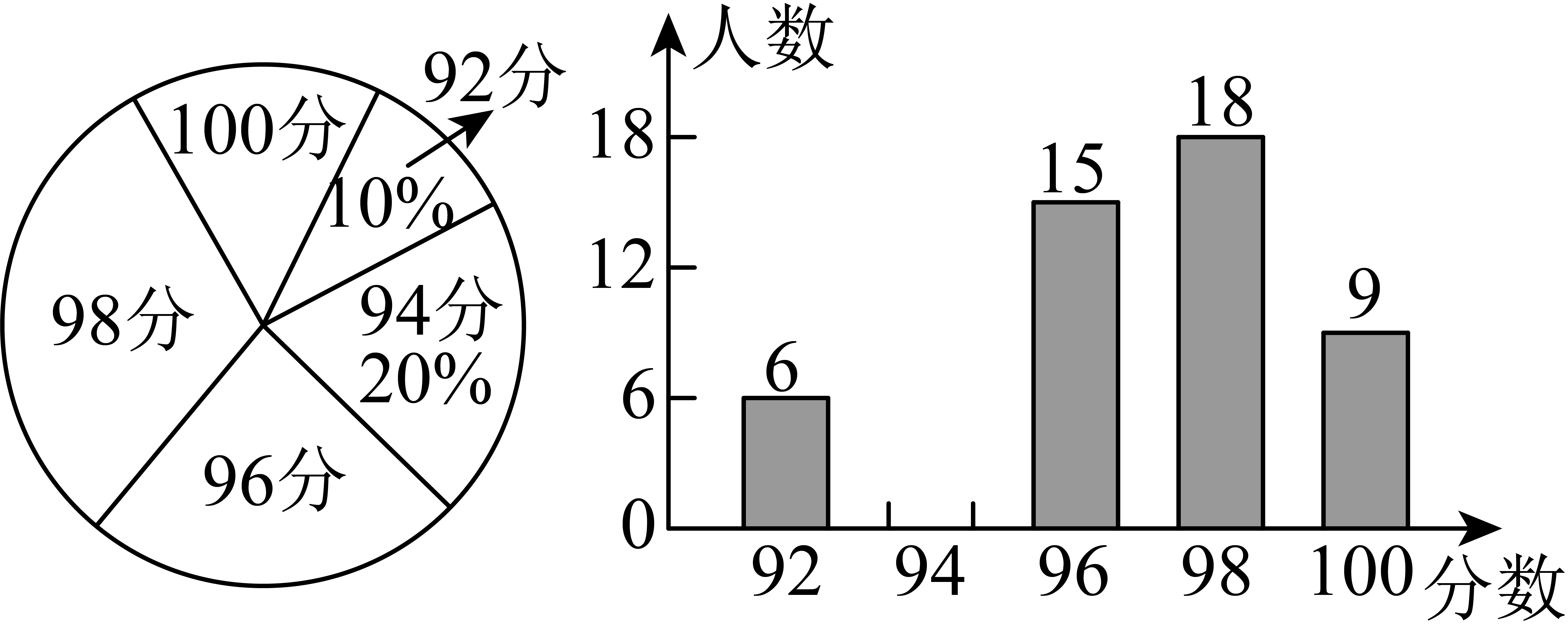
请根据统计图回答下列问题:
(1)、补全上面不完整的条形统计图.(2)、直接写出这些学生成绩的中位数和众数.(3)、根据比赛规则,98分及以上(含98分)的学生有资格进入第二轮知识竞赛环节,请你估计全校1200名学生进入第二轮知识竞赛环节的人数是多少?19. 某同学尝试在已知的中利用尺规作出一个菱形,如图所示.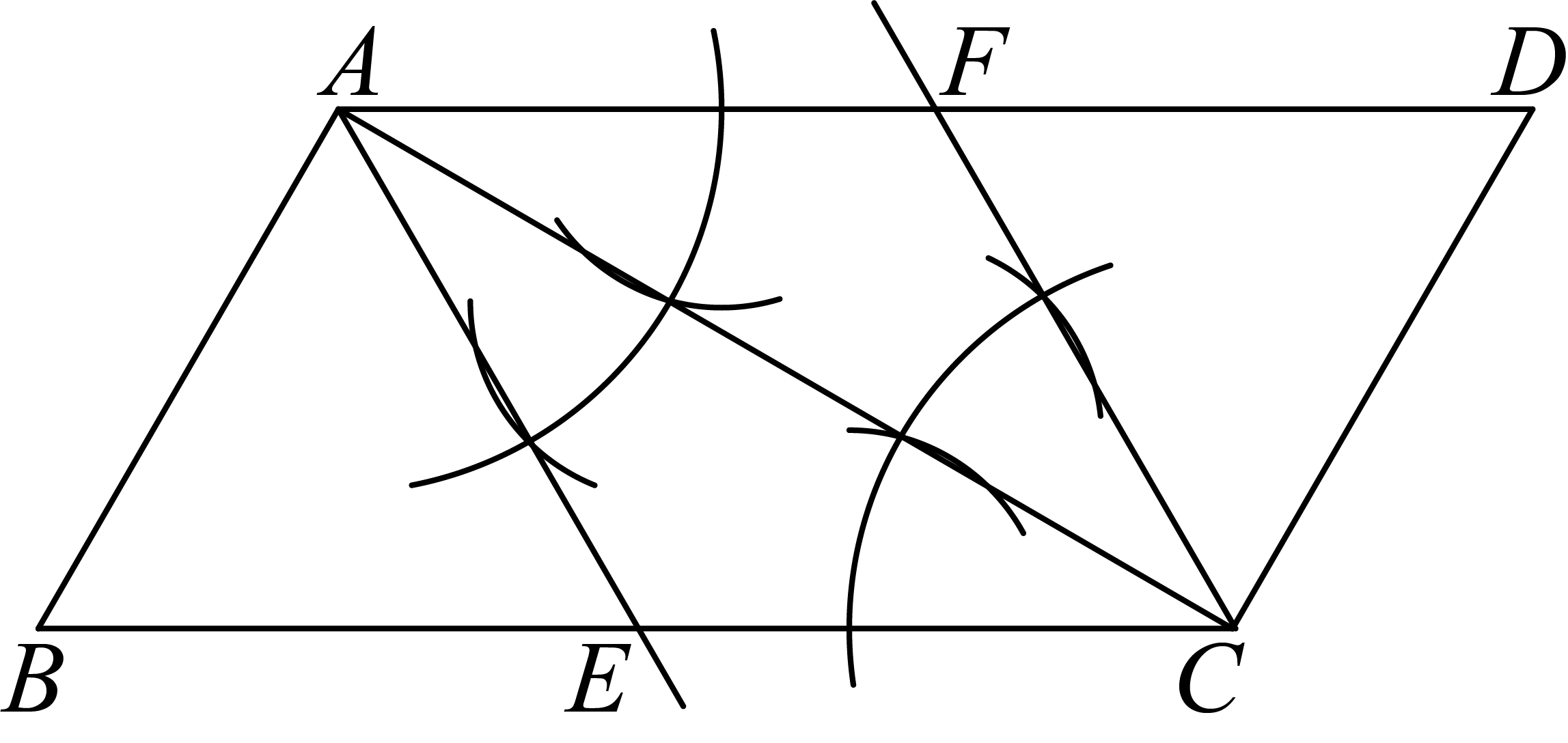 (1)、根据作图痕迹,能确定四边形是菱形吗?请说明理由.(2)、若 , , , 求四边形的面积.20. 小丽家饮水机中原有水的温度为20℃,通电开机后,饮水机自动开始加热,此过程中水温y(℃)与开机时间x(分)满足一次函数关系,当加热到100℃时自动停止加热,随后水温开始下降,此过程中水温y(℃)与开机时间x(分)成反比例关系,当水温降至20℃时,饮水机又自动开始加热……,重复上述程序(如图所示),根据图中提供的信息,解答问题:
(1)、根据作图痕迹,能确定四边形是菱形吗?请说明理由.(2)、若 , , , 求四边形的面积.20. 小丽家饮水机中原有水的温度为20℃,通电开机后,饮水机自动开始加热,此过程中水温y(℃)与开机时间x(分)满足一次函数关系,当加热到100℃时自动停止加热,随后水温开始下降,此过程中水温y(℃)与开机时间x(分)成反比例关系,当水温降至20℃时,饮水机又自动开始加热……,重复上述程序(如图所示),根据图中提供的信息,解答问题: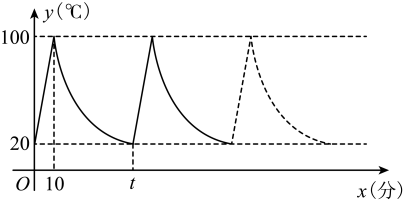 (1)、当时,求水温y(℃)与开机时间x(分)的函数关系式;(2)、求图中t的值;(3)、若小丽在通电开机后即外出散步,请你预测小丽散步70分钟回到家时,饮水机内的温度约为多少℃?21. 如图, , 点E在边上,以为斜边,在上方作 , 使 , 延长与交于点G .
(1)、当时,求水温y(℃)与开机时间x(分)的函数关系式;(2)、求图中t的值;(3)、若小丽在通电开机后即外出散步,请你预测小丽散步70分钟回到家时,饮水机内的温度约为多少℃?21. 如图, , 点E在边上,以为斜边,在上方作 , 使 , 延长与交于点G . (1)、当时,若 , 求线段的长.(2)、求证:点F为线段的中点.22. 如图,玻璃桌面与地面平行、桌面上有一盏台灯和一支铅笔,点光源O与铅笔所确定的平面垂直于桌面.在灯光照射下,在地面上形成的影子为(不计折射), .
(1)、当时,若 , 求线段的长.(2)、求证:点F为线段的中点.22. 如图,玻璃桌面与地面平行、桌面上有一盏台灯和一支铅笔,点光源O与铅笔所确定的平面垂直于桌面.在灯光照射下,在地面上形成的影子为(不计折射), . (1)、在桌面上沿着方向平移铅笔,试说明的长度不变.(2)、桌面上一点P恰在点O的正下方,且 , , , 桌面的高度为 . 在点O与所确定的平面内,将绕点A旋转,使得的长度最大.
(1)、在桌面上沿着方向平移铅笔,试说明的长度不变.(2)、桌面上一点P恰在点O的正下方,且 , , , 桌面的高度为 . 在点O与所确定的平面内,将绕点A旋转,使得的长度最大.①画出此时所在位置的示意图;
②的长度的最大值为 ▲ cm.