湖北省新中考G9联盟2024年九年级数学第一次模拟考试试卷

试卷更新日期：2024-04-19 类型：中考模拟

进入出卷网下载

一、单选题

1. 若a与1互为相反数，则 $a + 1 =$ （）

A、－1 B、0 C、2 D、1

查看试题解析
2. 下列图形中，是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 下列计算正确的是（）

A、 $(2 x^{2} y)^{2} = 4 x^{4} y^{2}$ B、 $x^{3} \div x = x^{3}$ C、 $2 x + 3 y = 5 x y$ D、 $(x + y)^{2} = x^{2} + y^{2}$

查看试题解析
4. 如图，将一副三角板叠放在一起，使直角顶点重合于O点，则∠AOC+∠DOB=（）

A、180° B、90° C、270° D、150°

查看试题解析
5. 五一期间，某商场设计了一个“玩转盘，享优惠”活动：如图所示的转盘盘面被分成四个相等的扇形区域，并分别标有文字满江红、红旗渠、殷墟、大峡谷．若转动转盘两次，每次转盘停止后指针所指区域都是“满江红”，将获得一张优惠券（当指针恰好指在分界线上时重转）．小王转动转盘两次，获得优惠券的概率为（）

A、 $\frac{1}{4}$ B、 $\frac{1}{8}$ C、 $\frac{1}{12}$ D、 $\frac{1}{16}$

查看试题解析
6. 如图所示四个立体图形，从正面看到的平面图形是四边形的个数是（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
7. 已知实数 $x_{1}$ ， $x_{2}$ 满足 $x_{1} + x_{2} = 7$ ， $x_{1} x_{2} = 12$ ，则以 $x_{1}$ ， $x_{2}$ 为根的一元二次方程是（）

A、 $x^{2} - 7 x + 12 = 0$ B、 $x^{2} + 7 x + 12 = 0$ C、 $x^{2} + 7 x - 12 = 0$ D、 $x^{2} - 7 x - 12 = 0$

查看试题解析
8. 如图， $P A ， P B$ 是 $⊙ O$ 的切线，A ， B是切点．若 $∠ P = 50 °$ ，则 $∠ A O B$ 的度数为（）

A、 $120 °$ B、 $130 °$ C、 $135 °$ D、 $150 °$

查看试题解析
9. 如图，坐标平面内一点 $A (3, - 2)$ ， O为原点，P是x轴上的一个动点，如果以点P、O、A为顶点的三角形是等腰三角形，那么符合条件的动点P的个数为（）

A、2 B、3 C、4 D、1

查看试题解析
10. 如图，二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的图像的顶点在第一象限，且过点 $(0, 1)$ 和 $(- 1, 0)$ ，下列结论：① $c = 1$ ；② $a b < 0$ ；③ $a - b + c = 0$ ；④当 $x > - 1$ 时， $y > 0$ ．其中正确结论的个数是（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 分解因式： $4 (m - n) m^{2} + (n - m) n^{2} =$ ．

查看试题解析
12. 若一组数据 $x_{1}, x_{2}, x_{3}, x_{4}, x_{5}$ 的平均数为4，则 $x_{1} + 2, x_{2} + 2, x_{3} + 2, x_{4} + 2, x_{5} + 2$ 的平均数为．

查看试题解析
13. 已知不等式组 ${\begin{array}{l} x \geq - a - 1 ① \\ - x \geq - b ② \end{array}$ ，在同一条数轴上表示不等式①，②的解集如图所示，则b﹣a的值为．

查看试题解析
14. 在矩形 $A B C D$ 中， $A B = 10$ ， $A D = 8$ ，点N是线段 $B C$ 的中点，点E ， G分别为射线 $D A$ ，线段 $A B$ 上的动点， $C E$ 交以 $D E$ 为直径的圆于点M ，则 $G M + G N$ 的最小值为．

查看试题解析
15. 请观察： $- \frac{1}{2}$ 、1、 $- \frac{9}{8}$ 、1、 $- \frac{25}{32}$ 、……则第100个数是.

查看试题解析

三、解答题

16. 计算：

(1)、 $(- 3) - | - 8 | - 2 \times (- 4)$ ；

(2)、 $- 1^{4} - \frac{1}{2} \times [3 - (- 3)^{2}]$ ．

查看试题解析
17. 先化简，再求值； $\frac{x^{2} - 2 x y + y^{2}}{x^{2} - y^{2}} \div \frac{x^{2} - x y}{x} - \frac{x}{x + y}$ ，其中x、y满足 $(x + 2)^{2} + \sqrt{y - 3}$ ＝0

查看试题解析
18. 如图，在矩形ABCD中，E是AB的中点，连接DE、CE.

求证：△ADE≌△BCE.

查看试题解析
19. 某校在一次大课间活动中，采用了四种活动形式：A、跑步，B、跳绳，C、做操，D、游戏．全校学生都选择了一种形式参与活动，小杰对同学们选用的活动形式进行了随机抽样调查，根据调查统计结果，绘制了不完整的统计图．
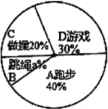
请结合统计图，回答下列问题：

(1)、本次调查学生共 ▲ 人， $a =$ ▲ ，并将条形图补充完整；

(2)、如果该校有学生2000人，请你估计该校选择“跑步”这种活动的学生约有多少人？

(3)、学校让每班在A、B、C、D四种活动形式中，随机抽取两种开展活动，请用树状图或列表的方法，求每班抽取的两种形式恰好是“跑步”和“跳绳”的概率．

查看试题解析
20. 一次函数 $y = 2 x + 2$ 与x轴交于C点，与y轴交于B点，点 $A (2, a)$ 在直线 $B C$ 上，反比例函数 $y = \frac{k}{x}$ 过点A ．

(1)、求a与k的值；

(2)、在x轴上是否存在点D ，使得 $∠ B O A = ∠ O A D$ ，若存在，请直接写出点D坐标；若不存在，请说明理由．

查看试题解析
21. 如图，在三角形 $A B C$ 中， $∠ B A C = 30 °$ ，以 $A B$ 为直径的圆 $O$ 经过点 $C$ ，过点 $C$ 作圆 $O$ 的切线交 $A B$ 延长线于点 $P$ ，点 $D$ 是圆上一点，点 $C$ 是劣弧 $B D$ 的中点，弦 $A B$ 的延长线交切线 $P C$ 于点 $E$ ，

(1)、判断 $O B$ 于 $B P$ 的数量关系并证明；

(2)、若 $A E = 3$ ，求圆 $O$ 的半径．

查看试题解析
22. 崇阳县“众望科工贸有限公司”生产的“众望小麻花”色香味美，老少皆宜，深受消费者青睐，“青嬣超市”从该公司购进“众望小麻花”进行销售，每箱进价30元，超市将销售价定为每箱40元时，每月可以卖出100箱，销售一段时间后发现，销售价每箱提高5元，每月就会少卖10箱．

(1)、直接写出每月的销售量y（箱）与销售价格x（元/箱）之间的关系式；

(2)、“青嬣超市”计划涨价销售，请你帮助超市计算一下，每箱销售价格为多少时，每月的销售利润最大，最大月销售利润为多少？

(3)、疫情期间，相关部门严格督查稳定物价，要求超市的利润不得超过平时的 $100 ％$ ，可由于防控交通不便等原因，“众望科工贸有限公司”的生产成本提高，“青嬣超市”的每箱麻花进价上涨了a元，该期间月销售量与销售价格仍然满足（1）中的函数关系，结果当月超市获得最大销售利润 $1500$ 元，求a的值．

查看试题解析
23.

(1)、【问题初探】数学课上，李老师出示了这样一个问题：如图1，在 $△ A B C$ 中， $A B = A C$ ，点F是 $A C$ 上一点，点E是 $A B$ 延长线上的一点，连接 $E F$ ，交 $B C$ 于点D ，若 $E D = D F$ ，求证： $B E = C F$ ．
①如图2，小乐同学从中点的角度，给出了如下解题思路：在线段 $D C$ 上截取 $D M$ ，使 $D M = B D$ ，连接 $F M$ ，利用两个三角形全等和已知条件，得出结论；
②如图3，小亮同学从平行线的角度给出了另一种解题思路：过点E作 $E M ∥ A C$ 交 $C B$ 的延长线于点M ，利用两个三角形全等和已知条件，得出了结论；
请你选择一位同学的解题思路，写出证明过程；

(2)、【类比分析】李老师发现两位同学的做法非常巧妙，为了让同学们更好的理解这种转化的思想方法，李老师提出了新的问题，请你解答，
如图4，在 $△ A B C$ 中，点E在线段 $A B$ 上，D是 $B C$ 的中点，连接 $C E$ ， $A D$ ， $C E$ 与 $A D$ 相交于点N ，若 $∠ E A D + ∠ A N C = 180 °$ ，求证： $A B = C N$ ；

(3)、【学以致用】如图5，在 $R t △ A B C$ 中， $∠ B A C = 90 °$ ， $∠ C = 30 °$ ， $A F$ 平分 $∠ B A C$ ，点E在线段 $B A$ 的延长线上运动，过点E作 $E D ∥ A F$ ，交 $A C$ 于点N ，交 $B C$ 于点D ，且 $B D = C D$ ，请直接写出线段 $A E$ ， $C N$ 和 $B C$ 之间的数量关系．

查看试题解析
24. 如图，已知抛物线交x轴于点A和点B ，交y轴于点C ，对称轴为直线 $x = - 1$ ， $A (1, 0) ， C (0, 3)$ ．

(1)、求抛物线的解析式和B点的坐标；

(2)、点P为抛物线在线段 $B C$ 上方的一个动点，点P的横坐标为m ．
①若 $S_{△ A B P} = 7$ ，求m的值；
②过点P作x轴的垂线，交线段 $B C$ 于点D ，线段 $P D$ 的长记为d ，求出d关于m的函数解析式，并计算d的最大值．

查看试题解析