湖北省黄石市阳新县城区四校2023-2024学年九年级下学期数学3月月考联考试卷

试卷更新日期：2024-04-19 类型：月考试卷

进入出卷网下载

一、选择题（共10小题，每小题3分，共30分）

1. $2024$ 的相反数是（）

A、 $\frac{1}{2024}$ B、 $- \frac{1}{2024}$ C、 $2024$ D、 $- 2024$

查看试题解析
2. 我国古代典籍《周易》中的“八卦”思想对我国建筑有一定的影响．如图是受“八卦”的启示，创作的正八边形窗户平面图，则对该图的对称性表述正确的是（）

A、只是轴对称图形 B、只是中心对称图形 C、既是轴对称图形，又是中心对称图形 D、既不是轴对称图形，又不是中心对称图形

查看试题解析
3. 如图所示，已知AB∥CD，EF平分∠CEG，∠1＝80°，则∠2的度数为（）

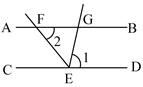A、20° B、40° C、50° D、60°

查看试题解析
4. 下列计算正确的是（　　）

A、3x+3y=6xy B、a²•a³=a⁶ C、b⁶÷b³=b² D、（m²）³=m⁶

查看试题解析
5. 如图是由3个相同的小正方体搭成的几何体，那么这个几何体的俯视图是（）

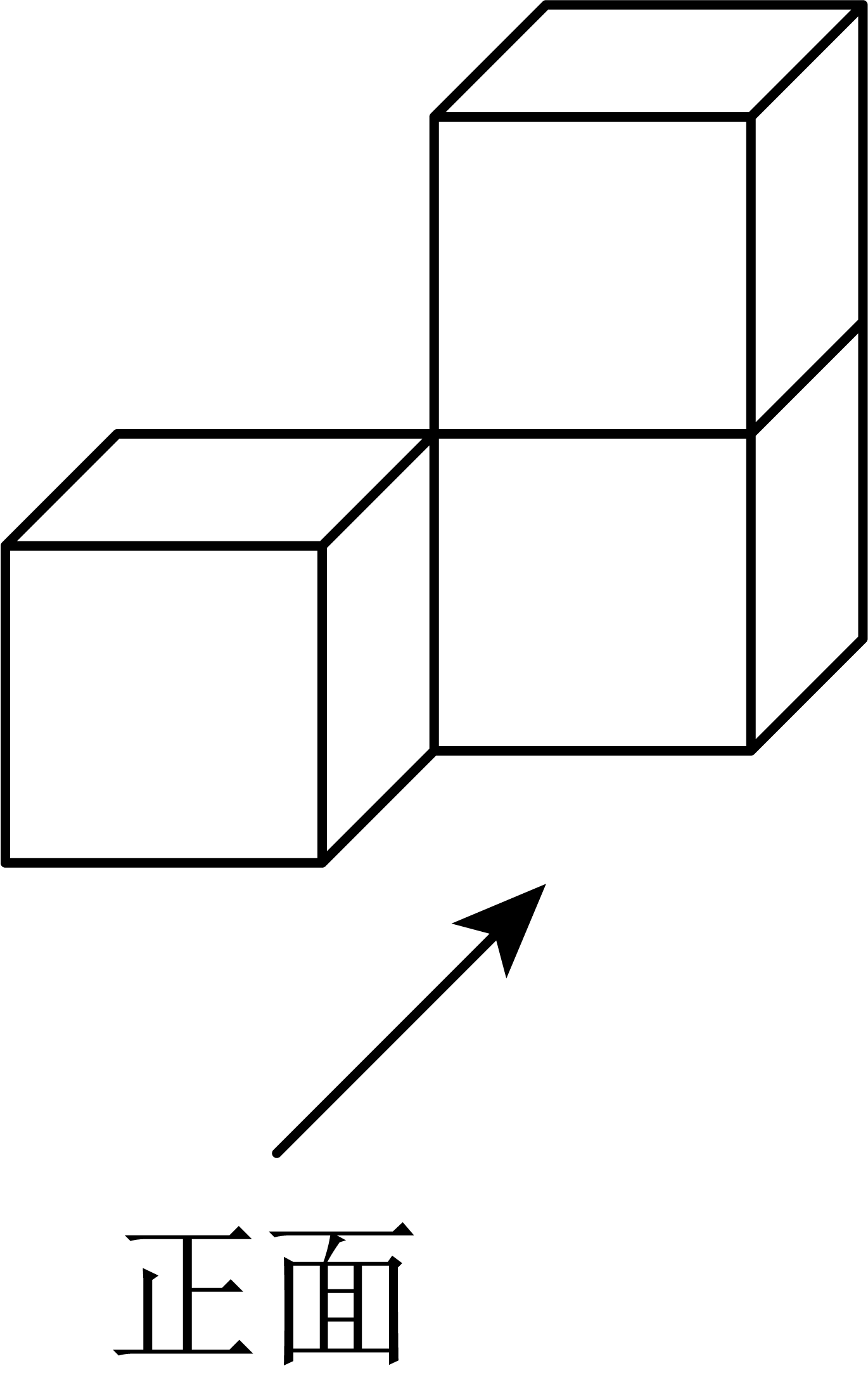A、 B、 C、 D、

查看试题解析
6. 下列说法正确的是（）

A、成语“刻舟求剑”描述的是必然事件 B、了解央视春晚的收视率适合用抽样调查 C、调查某品牌烟花的合格率适合用全面调查 D、如果某彩票的中奖率是1%，那么一次购买100张彩票一定会中奖

查看试题解析
7. 图中表示被撕掉一块的正n边形纸片，若 $\vec{a} ⊥ \vec{b}$ （即延长a和b相交形成的），则n的值是（）

A、6 B、8 C、10 D、12

查看试题解析
8. 分式方程 $\frac{x}{x - 1} - 1 = \frac{3}{(x - 1) (x + 2)}$ 的解是（）

A、x=1 B、x=﹣1+ $\sqrt{5}$ C、x=2 D、无解

查看试题解析
9. 木匠师傅用长 $A B = 3$ ，宽 $B C = 2$ 的矩形木板做一个尽可能大的圆形桌面，有如下两种方案：
方案一：直接锯一个半径最大的圆；
方案二：沿对角线 $A C$ 将矩形锯成两个三角形，适当平移三角形并锯一个最大的圆．则方案二比方案一的半径大（）

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{1}{4}$ D、 $\frac{1}{5}$

查看试题解析
10. 如图所示，二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的图象的对称轴是直线 $x = 1$ ，且经过点 $(0, 2)$ ，有下列结论：① $a b c > 0$ ；② $a + b \geq m (a m + b) (m$ 为常数）；③若 $(2, y_{1})$ ， $(\frac{1}{2}, y_{2})$ ， $(- 2, y_{3})$ 在该函数图象上，则 $y_{3} < y_{1} < y_{2}$ ；④ $- \frac{2}{3} < a < - \frac{1}{4}$ ．其中正确的个数是（）

A、1 B、2 C、3 D、4

查看试题解析

二、填空题（本大题共6小题，每小题3分，满分18分．请把答案填在答题卡相应题号的横线上）

11. 截止2021年4月中国高速路总里程达16万公里.请将“16万”用科学记数法表示记为.

查看试题解析
12. 在物理课上，某实验的电路图如图所示，其中S₁ ， S₂ ， S₃表示电路的开关，L表示小灯泡，R为保护电阻．若闭合开关S₁ ， S₂ ， S₃中的任意两个，则小灯泡L发光的概率为．

查看试题解析
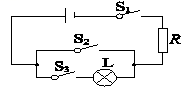13. 如图是某商场营业大厅自动扶梯的示意图 $.$ 自动扶梯 $A B$ 的倾斜角为 $37 °$ ，大厅两层之间的距离 $B C$ 为 $6$ 米，则自动扶梯 $A B$ 的长约为 $. (s i n 37 ° \approx 0.6, c o s 37 ° \approx 0.8, t a n 37 ° \approx 0.75)$

查看试题解析
14. 小明学习相交直线时发现：3条直线两两相交最多有3个交点，4条直线两两相交最多有6个交点，按照这样的规律，

(1)、5条直线两两相交最多有个交点；

(2)、n条直线两两相交最多有个交点．（用含有字母n的式子表示， $n \geq 3$ ）

查看试题解析
15. PA，PB，CD是⊙O的切线，A，B，E是切点，CD分别交PA，PB于C，D两点，若∠APB=50°，则∠COD的度数为.

查看试题解析
16. 《九章算术》是人类科学史上应用数学的“算经之首”，书中记载：今有三人共车，二车空；二人共车，九人步．问：人与车各几何？译文：若3人坐一辆车，则两辆车是空的；若2人坐一辆车，则9人需要步行，问：人与车各多少？根据题意，可求得共有人．

查看试题解析

三、解答题（共8小题，共72分．解答应写出文字说明、演算步骤或推理过程）

17. 解不等式组 ${\begin{array}{l} 2 x + 1 < - 1 ① \\ 3 x + 5 \geq x ② \end{array}$ ，请按下列步骤完成解答：

(1)、解不等式①，得；

(2)、解不等式②，得；

(3)、把不等式①和②的解集在数轴上表示出来；

(4)、原不等式组的解集为．

查看试题解析
18. 如图，在□ABCD中，对角线AC ， BD相交于点O ，且OA＝OB＝5，AB＝6，求□ABCD的面积．

查看试题解析
19. 如图， $A E ∥ B F$ ， $A C$ 平分 $∠ B A E$ 交 $B F$ 于点C ．

(1)、作 $∠ A B F$ 的平分线交 $A E$ 于点D（尺规作图，保留痕迹，不写作法）；

(2)、根据（1）中作图，连接 $C D$ ，判断四边形 $A B C D$ 的形状并证明．

查看试题解析
20. 甲、乙两座城市的中心火车站A ， B两站相距360km．一列动车与一列特快列车分别从A ， B两站同时出发相向而行，动车的平均速度比特快列车快 $54 k m / h$ ，当动车到达B站时，特快列车恰好到达距离A站135km处的C站．求动车和特快列车的平均速度各是多少？

查看试题解析
21. 如图，过矩形 $A B C D$ 顶点A ， B的圆O与 $C D$ 相切于点G ， $B C$ 分别相交于点F ， E ，连接 $A E$ ．

(1)、求证： $E G$ 平分 $∠ C E A$ ；

(2)、若 $A B = 3$ ， $B E = 4$ ，求 $G E$ 的长．

查看试题解析
22. 如图，海面上一艘船由西向东航行，在A处测得正东方向上一座灯塔的最高点C的仰角为31°，再向东继续航行60m到达B处，测得该灯塔的最高点C的仰角为45°.根据测得的数据，计算这座灯塔的高度CD（结果取整数）.参考数据：sin31°≈0.52，cos31°≈0.86，tan31°≈0.60

查看试题解析
23. 如图1，抛物线 $y = a x^{2} + b$ 与 $x$ 轴交于A、B两点，与 $y$ 轴交于点 $C$ ，点 $A$ 的坐标是 $(2 ， 0)$ ，点 $C$ 的坐标是 $(0 ， 4)$ ．

(1)、求抛物线的解析式；

(2)、如图2，点 $P$ 是第四象限内抛物线上一点，连接 $P B$ 交 $y$ 轴于点 $E$ ，设点 $P$ 的横坐标为，线段 $C E$ 的长为d ，求d与之间的函数关系式，并直接写出自变量的取值范围；

(3)、如图3，点 $D$ 是第三象限内抛物线上一点，连接 $P D$ 交 $y$ 轴于点 $F$ ，过点 $D$ 作 $D M ⊥ B P$ 于点 $H$ ，交 $x$ 轴于点 $M$ ，连接 $A D$ 交 $B P$ 于点 $N$ ，连接 $M N$ ，若 $E F = \frac{d}{2}$ ， $∠ B N D = ∠ A N M$ 时，求点 $P$ 的坐标．

查看试题解析