【培优卷】2024年浙教版数学七年级下册第5章分式单元测试

试卷更新日期：2024-04-18 类型：单元试卷

进入出卷网下载

一、选择题（每题3分，共30分）

1. 若关于x的分式方程 $\frac{2 a + 1}{x + 1} = a$ 有增根，则a的值为（）

A、 $- \frac{1}{2}$ B、0 C、 $- \frac{1}{2}$ 或0 D、-1或 $- \frac{1}{2}$

查看试题解析
2. 已知 $a + \frac{1}{a} = \sqrt{10} ，$ 则 $\frac{a^{2} - 1}{a}$ 的值为（）

A、8 B、 $\sqrt{6}$ C、±2 $\sqrt{2}$ . D、± $\sqrt{6}$

查看试题解析
3. 已知分式 $A = \frac{4}{x^{2} - 4} ， B = \frac{1}{x + 2} - \frac{1}{x - 2} ，$ 则A与B的关系是（）

A、A=B B、A=-B C、A>B D、A<B

查看试题解析
4. 若实数a，b，c，d满足号 $\frac{a}{b} = \frac{b}{c} = \frac{c}{d} = \frac{d}{a}$ ，则 $\frac{a b + b c + c d + d a}{a^{2} + b^{2} + c^{2} + d^{2}}$ 的值为（）

A、1或0 B、-1或0 C、1或-2 D、1或-1

查看试题解析
5. 已知关于 $x$ 的分式方程 $\frac{m}{x - 1} = 2 + \frac{x}{1 - x}$ 的解为非负数，则 $m$ 的取值范围是（）

A、 $m \geq - 2$ 且 $m \neq - 1$ B、 $m \leq 2$ 月 $m \neq 1$ C、 $m \geq - 2$ 且 $m \neq 1$ D、 $m \leq 2$ 且 $m \neq - 1$

查看试题解析
6. 若 $p = \frac{1}{n (n + 2)} + \frac{1}{(n + 2) (n + 4)} + \frac{1}{(n + 4) (n + 6)}$ $+ \frac{1}{(n + 6) (n + 8)} + \frac{1}{(n + 8) (n + 10)} ，$ 则使 p的值最接近 $\frac{1}{10}$ 的正整数 n是（）

A、4 B、5 C、6 D、7

查看试题解析
7. 甲打字员原计划单独用若干小时完成文稿的电脑输入工作，2 h后，乙打字员协助此项工作，且乙打字员文稿电脑输入的速度是甲的1.5倍，结果提前6h完成任务，则甲打字员原计划完成此项工作的时间是（）

A、17 h B、14 h C、12 h D、10 h

查看试题解析
8. 张华在一次数学活动中，利用“在面积一定的长方形中，正方形的周长最短”的结论，推导出“式子x+ $\frac{1}{x}$ (x>0)的最小值是2？其推导方法如下：在面积为1的长方形中，设长方形的一边长为x，则另一边长是 $\frac{1}{x}$ ，长方形的周长是2(x+ $\frac{1}{x}$ )；当长方形成为正方形时，就有x= $\frac{1}{x}$ (x>0)，解得x=1，这时长方形的周长2(x+ $\frac{1}{x}$ )=4最小，因此x+ $\frac{1}{x}$ (x>0)的最小值是2．模仿张华的推导，你求得式子 $\frac{x^{2} + 9}{x}$ (x>0)的最小值是（）．

A、2 B、1 C、6 D、10

查看试题解析
9. 某工程队需要铺设一条长为2400米的公路，铺设时“...”，设原计划每天铺设 $a$ 米，可得方程 $\frac{2400}{a} - \frac{2400}{a + 20} = 6$ ，根据此情景，题中用“...”表示的缺失条件应补为（）

A、实际每天铺设比原计划多铺设20米，结果提前6天完成 B、实际每天铺设比原计划少铺设20米，结果提前6天完成 C、实际每天铺设比原计划多铺设20米，结果延期6天完成 D、实际每天铺设比原计划少铺设20米，结果延期6天完成

查看试题解析
10. 老师设计了接力游戏，通过合作的方式完成分式的化简.规则：每人只能看到前一人给的式子，并进行一步计算，再将结果传递给下一人，最后完成化简，过程如图所示.接力中，自己负责的一步出现错误的是（）

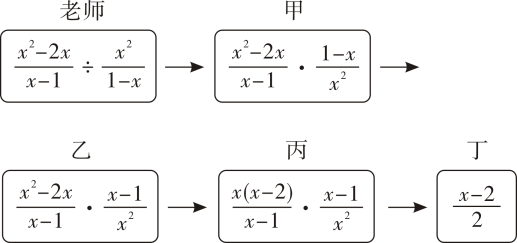A、只有乙 B、甲和丁 C、乙和丙 D、乙和丁

查看试题解析

二、填空题（每题4分，共24分）

11. 若 $x^{2} - 3 x + 1 = 0$ ，则 $\frac{x^{2}}{x^{4} + x^{2} + 1}$ 的值为

查看试题解析
12. 若方程 $\frac{2}{1 - x} = \frac{x}{x - 1} - 3$ 的解为 $x = \frac{5}{2}$ ，则方程 $\frac{2}{1 - 2 y} = \frac{2 y}{2 y - 1} - 3$ 的解为 $y =$ ．

查看试题解析
13. 一房屋设计图原房间窗户面积为3m² ，地面面积为18m² ，该住户要求把房间的窗户和地面都增加相同的整数面积（单位：m²）的方式加强采光效果，并使窗户面积与地面面积的比值尽可能接近 $\frac{1}{3}$ ，则增加的面积为m² ．

查看试题解析
14. 有一并联电路，如图所示，两电阻阻值分别为 $R_{1}$ ， $R_{2}$ ，总电阻值为 $R$ ，三者关系为： $\frac{1}{R} = \frac{1}{R_{1}} + \frac{1}{R_{2}}$ ．若已知 $R$ ， $R_{2}$ ，则 $R_{1} =$ ．

查看试题解析
15. 某次列车平均提速 $v km / h$ ，用相同的时间，列车提速前行驶 $s km$ ，提速后比提速前多行驶 $50 m$ .设提速前列车的平均速度是 $x km / h$ .根据题意分别列出下列四个方程：① $\frac{s}{x} = \frac{s + 50}{x + v}$ ；② $\frac{s}{x + v} = \frac{s + 50}{x}$ ；③ $\frac{x}{x + v} = \frac{s}{s + 50}$ ；④ $\frac{s}{x} = \frac{50}{v}$ .则其中正确的方程有.(填序号)

查看试题解析
16. 一组按规律排列的式子： $- \frac{b^{2}}{a}$ ， $\frac{b^{5}}{a^{2}}$ ， $- \frac{b^{8}}{a^{3}}$ ， $\frac{b^{11}}{a^{4}}$ ，…（ab≠0），其中第7个式子是，第n个式子是（n为正整数）．

查看试题解析

三、解答题（共8题，共66分）

17. （1）计算： $- 2^{2} + 202 3^{0} + \frac{3^{3} + 3^{4}}{3^{3}}$ ；

(1)、先化简，再求值： $(1 - \frac{2}{x - 1}) \div \frac{x^{2} - 6 x + 9}{x^{2} - 1}$ ，其中x从1，2，3中选一个你喜欢的值代入．

查看试题解析
18.

(1)、【探索】
①如果 $\frac{3 x + 4}{x + 1} = 3 + \frac{m}{x + 1}$ ，则 $m =$ .

②如果 $\frac{5 x - 3}{x + 2} = 5 + \frac{m}{x + 2}$ ，则 $m =$ .

(2)、【总结】如果 $\frac{a x + b}{x + c} = a + \frac{m}{x + c}$ (其中a，b，c为常数)，则m=.

(3)、【应用】利用上述结论解决：若代数式 $\frac{4 x - 3}{x - 1}$ 的值为整数，求满足条件的整数 $x$ 的值.

查看试题解析
19. 先阅读下面的材料，然后回答问题：
方程x+ $\frac{1}{x}$ =2+ $\frac{1}{2}$ 的解为x₁=2，x₂= $\frac{1}{2}$ ；
方程x+ $\frac{1}{x}$ =3+ $\frac{1}{3}$ 的解为x₁=3，x₂= $\frac{1}{3}$ ；
方程x+ $\frac{1}{x}$ =4+ $\frac{1}{4}$ 的解为x₁=4，x₂= $\frac{1}{4}$
……

(1)、观察上述方程的解，猜想关于x的方程x+ $\frac{1}{x}$ =5+ $\frac{1}{5}$ 的解是.

(2)、根据上面的规律，猜想关于x的方程x+ $\frac{1}{x}$ =a+ $\frac{1}{a}$ 的解是.

(3)、猜想关于x的方程x- $\frac{1}{x}$ = $1 \frac{1}{2}$ 的解并验证你的结论

(4)、在解方程y+ $\frac{y + 2}{y + 1}$ = $\frac{10}{3}$ 时，可将方程变形转化为(2)的形式求解，按要求写出你的变形求解过程．

查看试题解析
20. 阅读材料：小明发现像 $m + n$ ， $\frac{1}{m} + \frac{1}{n}$ ， $m^{2} + n^{2}$ 等代数式，如果任意交换两个字母的位置，式子的值都不变.太神奇了！于是他把这样的式子命名为神奇对称式，他还发现像 $m^{2} + n^{2}$ ， $\frac{1}{m} + \frac{1}{n}$ 等神奇对称式都可以用 $m + n$ ， $m n$ 表示.
例如： $m^{2} + n^{2} = {(m + n)}^{2} - 2 m n$ ， $\frac{1}{m} + \frac{1}{n} = \frac{m + n}{m n}$ .

请根据以上材料解决下列问题：

(1)、① $\frac{1}{m n}$ ， ② $m^{2} - n^{2}$ ， ③ $\frac{n}{m}$ ， ④ $x y + y z + x z$ 中，是神奇对称式的有（填序号）；

(2)、已知 $(x - m) (x - n) = x^{2} - p x + q$ .
①若 $p = 3$ ， $q = 2$ ，则神奇对称式 $\frac{1}{m} + \frac{1}{n} =$ ；

②若 $q = \frac{1}{4}$ ，且神奇对称式 $m^{2} + n^{2} + \frac{1}{m} + \frac{1}{n}$ 的值为 $- \frac{1}{2}$ ，求 $p$ 的值.

查看试题解析
21. 甲、乙、丙三名打字员承担一项打字任务，已知信息如下：
信息一：甲单独完成任务所需时间比乙单独完成任务所需时间多5小时；
信息二：甲4小时完成的工作量与乙3小时完成的工作量相等；
信息三：丙的工作效率是甲的工作效率的2倍．
如果每小时只安排1名打字员，那么按照甲、乙、丙的顺序至完成工作任务，共需多长时间？

查看试题解析
22. 一项工程需要甲、乙两队完成，已知甲队单独完成需要48天，乙队单独完成需要60天．甲队先做12天，然后甲、乙两队合作完成剩下的工作．

(1)、甲、乙两队合作还需要多少天完成此项工作？

(2)、已知甲队每天的劳务费比乙队多30元，完成这项工程共需支付劳务费7200元．则甲、乙两队每天的劳务费各是多少元？

查看试题解析
23. 在数学学习过程中，通常是利用已有的知识与经验，通过对研究对象进行观察、实验、推理、抽象概括，发现数学规律，揭示研究对象的本质特征．
比如“同底数幂的乘法法则”的学习过程是利用有理数的乘方概念和乘法结合律，由“特殊”到“一般”进行抽象概括的：
2²×2³=2⁵ ， 2³×2⁴=2⁷ ， 2²×2⁶=2⁸…⇒2^m×2ⁿ=2^m+n…⇒a^m×aⁿ=a^m+n（m、n都是正整数）．
我们亦知： $\frac{2}{3} < \frac{2 + 1}{3 + 1}$ ， $\frac{2}{3} < \frac{2 + 2}{3 + 2}$ ， $\frac{2}{3} < \frac{2 + 3}{3 + 3}$ ， $\frac{2}{3} < \frac{2 + 4}{3 + 4}$ …

(1)、请你根据上面的材料，用字母a、b、c归纳出a、b、c（a＞b＞0，c＞0）之间的一个数学关系式．

(2)、试用（1）中你归纳的数学关系式，解释下面生活中的一个现象：“若m克糖水里含有n克糖，再加入k克糖（仍不饱和），则糖水更甜了”．

查看试题解析

24. 在乐清某校的压花拓展课上，甲、乙两位同学每小时能共做7幅作品A，甲、乙同时开始制作，当甲做了28幅作品A时，乙做了21幅．

(1)、求甲、乙每小时各做多少幅作品A．

(2)、学校组织义拍资助西部贫困学生的活动，甲、乙两位同学计划共同完成30幅作品A参与义拍，并同时从13：00开始制作。（不考虑休息时间，每人做完一幅作品后才能做下一幅）．

①若甲完成的数量比乙完成的2倍少6幅，求在几时几分恰好全部完成．

②因义拍实际需要，现增加10幅作品B分配给甲、乙两位同学，并要求尽早完成制作，已知甲、乙每小时分别能做6幅和4幅作品B，请你结合方案评价表直接在表格中写出一种作品A，B的分配数量方案．

作品类型	作品A	作品B
分配给甲的数量
分配给乙的数
方案评价表
方案等级	完成时间	评分
合格	18：26~18：36	1分
良好	18：16~18：26	2分
优秀	18：16前	3分

查看试题解析

【培优卷】2024年浙教版数学七年级下册第5章分式 单元测试

一、选择题（每题3分，共30分）

二、填空题（每题4分，共24分）

三、解答题（共8题，共66分）

【培优卷】2024年浙教版数学七年级下册第5章分式单元测试