云南省文山州文山市第二学区2023-2024学年七年级下学期3月练习数学试题
试卷更新日期:2024-04-17 类型:月考试卷
一、选择题(本大题共15小题,每小题2分,共30分)
-
1. 下列各数是无理数的是( )A、 B、 C、0 D、2. 如图,与是对顶角的是( )A、
 B、
B、 C、
C、 D、
D、 3. 的立方根是( )A、 B、8 C、4 D、4. 两条直线被第三条直线所截,就第三条直线上的两个交点而言形成了“三线八角”.为了便于记忆,同学们可仿照图用双手表示“三线八角”(两大拇指代表被截直线,食指代表截线).下列三幅图依次表示( )
3. 的立方根是( )A、 B、8 C、4 D、4. 两条直线被第三条直线所截,就第三条直线上的两个交点而言形成了“三线八角”.为了便于记忆,同学们可仿照图用双手表示“三线八角”(两大拇指代表被截直线,食指代表截线).下列三幅图依次表示( ) A、同位角、同旁内角、内错角 B、同位角、内错角、同旁内角 C、同位角、对顶角、同旁内角 D、同位角、内错角、对顶角5. 下列各式中,正确的是( )A、 B、 C、 D、6. 如图所示,点E在AC的延长线上,下列条件能判断的是( )
A、同位角、同旁内角、内错角 B、同位角、内错角、同旁内角 C、同位角、对顶角、同旁内角 D、同位角、内错角、对顶角5. 下列各式中,正确的是( )A、 B、 C、 D、6. 如图所示,点E在AC的延长线上,下列条件能判断的是( ) A、 B、 C、 D、7. 9的平方根是( )A、 B、 C、3 D、818. 估计的值在( )A、2到3之间 B、3到4之间 C、4到5之间 D、5到6之间9. 已知实数满足 , 那么的值为( )A、 B、1 C、 D、210. 如图是小强同学一次立足跳远的示意图,小强从点B起跳,落到了点A处,若米,则小强的跳远成绩( )
A、 B、 C、 D、7. 9的平方根是( )A、 B、 C、3 D、818. 估计的值在( )A、2到3之间 B、3到4之间 C、4到5之间 D、5到6之间9. 已知实数满足 , 那么的值为( )A、 B、1 C、 D、210. 如图是小强同学一次立足跳远的示意图,小强从点B起跳,落到了点A处,若米,则小强的跳远成绩( ) A、2.37米 B、2.46米 C、2.51米 D、2.56米11. 下列命题是真命题的是( )A、互补的两个角是邻补角 B、过一点有且只有一条直线与已知直线垂直 C、对顶角相等 D、两条直线被第三条直线所截,内错角相等12. 如图 , 为之间的一点,已知 , , 则的度数为( )
A、2.37米 B、2.46米 C、2.51米 D、2.56米11. 下列命题是真命题的是( )A、互补的两个角是邻补角 B、过一点有且只有一条直线与已知直线垂直 C、对顶角相等 D、两条直线被第三条直线所截,内错角相等12. 如图 , 为之间的一点,已知 , , 则的度数为( ) A、 B、 C、 D、13. 如图,将三角形ABC沿BC方向平移得到三角形DEF,若BC=4,EC=1,则平移的距离为( )
A、 B、 C、 D、13. 如图,将三角形ABC沿BC方向平移得到三角形DEF,若BC=4,EC=1,则平移的距离为( )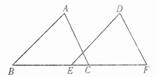 A、7 B、6 C、4 D、314. 已知 , 则的值为( )A、4 B、9 C、2 D、15. 在直线上取一点 , 过点作射线 , 使 , 当时,等于( )A、 B、 C、或 D、或
A、7 B、6 C、4 D、314. 已知 , 则的值为( )A、4 B、9 C、2 D、15. 在直线上取一点 , 过点作射线 , 使 , 当时,等于( )A、 B、 C、或 D、或二、填空题(本大题共4小题,每小题2分,共8分)
-
16. 2的相反数是 .17. 如图,直线与直线都相交.若 , , 则 .
 18. 比较大小:(填“ , 或”)19. 把命题“等角的余角相等”改写成“如果…,那么…”的形式为 .
18. 比较大小:(填“ , 或”)19. 把命题“等角的余角相等”改写成“如果…,那么…”的形式为 .三、解答题(本大题共8小题,共62分)
-
20. 如图,直线和相交于点 , 平分 , , , 求的度数。
 21. 计算:(1)、(2)、22. 如图,已知 , . 求证:
21. 计算:(1)、(2)、22. 如图,已知 , . 求证: 23. 如图,在方格纸内将三角形水平向右平移4个单位,再向下平移1个单位得到三角形 .
23. 如图,在方格纸内将三角形水平向右平移4个单位,再向下平移1个单位得到三角形 . (1)、画出平移后的三角形;(2)、过作线段的垂线直线 , 垂足为;(3)、图中与的关系是:;24. 已知一个正数的两个平方根分别为和(1)、求的值;(2)、求的立方根.25. 请完成下面的推理过程,并在括号内填写推理依据。
(1)、画出平移后的三角形;(2)、过作线段的垂线直线 , 垂足为;(3)、图中与的关系是:;24. 已知一个正数的两个平方根分别为和(1)、求的值;(2)、求的立方根.25. 请完成下面的推理过程,并在括号内填写推理依据。如图, , , 试判断与的大小关系,并证明你的结论。

解:与相等。证明如下:
▲ (已知)
(邻补角定义)
▲ (等量代换)
▲ (内错角相等,两直线平行)
( )
又(已知)
▲ ( )
▲ ( )
(两直线平行,同位角角相等)
26. 阅读下列材料:我们知道面积是5的正方形边长是 , 因为 , 且更接近于2,所以设 , 将正方形边长分为2与两部分,如图所示。由面积公式,可得 . 因为较小,略去 , 得方程 , 解得 (1)、阅读上述材料,可以得到;(2)、请类比所给方法,探究的近似值。
(1)、阅读上述材料,可以得到;(2)、请类比所给方法,探究的近似值。(画出示意图,表明数据,并写出求解过程,结果保留两位小数)
27. 小明对一副直角三角板在平行线间的位置进行研究,已知 .图①
 图②
图② 图③
图③ (1)、如图①,小明将含角的直角三角板中的点A落在直线上,若 , 则的度数为;(2)、如图②,小明将含角的直角三角板DEF中的点D , F分别落在直线上,若DE平分 , 则EF是否平分?请说明理由.(3)、小明将三角板与三角板按如图③所示方式摆放,点B与点F重合,求的度数.
(1)、如图①,小明将含角的直角三角板中的点A落在直线上,若 , 则的度数为;(2)、如图②,小明将含角的直角三角板DEF中的点D , F分别落在直线上,若DE平分 , 则EF是否平分?请说明理由.(3)、小明将三角板与三角板按如图③所示方式摆放,点B与点F重合,求的度数.