云南省文山壮族苗族自治州文山市2023-2024学年九年级下学期3月月考数学试题
试卷更新日期:2024-04-17 类型:月考试卷
一、选择题(本大题共15个小题,每小题只有一个正确选项,每小题2分,满分30分)
-
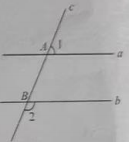
1. 冰箱保鲜室的温度零上记作 , 则冷冻室的温度零下记作( )A、 B、 C、 D、2. 文山州今年约有260000名七年级学生,数260000用科学记数法可表示为( )A、 B、 C、 D、3. 如图,直线 , 直线与 , 分别交于 , 两点,若 , 则的度数是( )
 A、 B、 C、 D、4. 已知反比例函数的图象经过点 , 则的值为( )A、 B、10 C、 D、75. 如图是某个几何体的三视图,该几何体是( ).
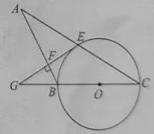
A、 B、 C、 D、4. 已知反比例函数的图象经过点 , 则的值为( )A、 B、10 C、 D、75. 如图是某个几何体的三视图,该几何体是( ).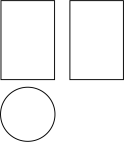 A、圆柱 B、圆锥 C、四棱柱 D、四棱锥6. 下列计算正确的是( )A、 B、 C、 D、7. 如图点、、都在上, , 的度数是( )
A、圆柱 B、圆锥 C、四棱柱 D、四棱锥6. 下列计算正确的是( )A、 B、 C、 D、7. 如图点、、都在上, , 的度数是( )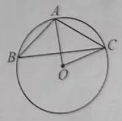 A、 B、 C、 D、8. 一个多边形内角和是 , 则这个多边形的边数为( )A、8 B、10 C、9 D、119. 下列四个图形中,属于轴对称图形的是( )A、
A、 B、 C、 D、8. 一个多边形内角和是 , 则这个多边形的边数为( )A、8 B、10 C、9 D、119. 下列四个图形中,属于轴对称图形的是( )A、 B、
B、 C、
C、 D、
D、 10. 若函数有意义,则的取值范围是( )A、 B、 C、 D、11. 如图,在中, , , , 为的中点,则等于( )
10. 若函数有意义,则的取值范围是( )A、 B、 C、 D、11. 如图,在中, , , , 为的中点,则等于( )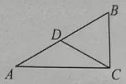 A、2 B、3.5 C、3 D、2.512. 《2024年春节联欢晚会》以匠心独运的歌舞创编、暖心真挚的节目表演、充满科技感和时代感的视觉呈现,为海内外受众奉上了一道心意满满、暖意融融的除夕“文化大餐”.截至2月10日2时,总台春晚全媒体累计触达142亿人次,其中“竖屏看春晚”直播播放量4.2亿次。据统计,2022年首次推出的“竖屏看春晚”累计观看2亿次,设“竖屏看春晚”次数的年平均增长率为 , 则可列出关于的方程( )A、 B、 C、 D、13. 某中学对延时服务选课意向进行了随机抽样调查,要求被调查者只能选择其中的一项,根据得到的数据,绘制不完整统计图如下,则下列说法中不正确的是( )
A、2 B、3.5 C、3 D、2.512. 《2024年春节联欢晚会》以匠心独运的歌舞创编、暖心真挚的节目表演、充满科技感和时代感的视觉呈现,为海内外受众奉上了一道心意满满、暖意融融的除夕“文化大餐”.截至2月10日2时,总台春晚全媒体累计触达142亿人次,其中“竖屏看春晚”直播播放量4.2亿次。据统计,2022年首次推出的“竖屏看春晚”累计观看2亿次,设“竖屏看春晚”次数的年平均增长率为 , 则可列出关于的方程( )A、 B、 C、 D、13. 某中学对延时服务选课意向进行了随机抽样调查,要求被调查者只能选择其中的一项,根据得到的数据,绘制不完整统计图如下,则下列说法中不正确的是( )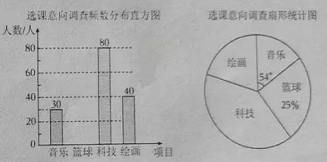 A、这次调查的样本容量是200 B、全校1200名学生中,估计选篮球课大约有400人 C、扇形统计图中,科技课所对应的圆心角是 D、被调查的学生中,选绘画课人数占比为14. 一列单项式按以下规律排列: , 则第2024个单项式是( )A、 B、 C、 D、15. 估计的值是在( )A、1到2之间 B、2到3之间 C、3到4之间 D、4到5之间
A、这次调查的样本容量是200 B、全校1200名学生中,估计选篮球课大约有400人 C、扇形统计图中,科技课所对应的圆心角是 D、被调查的学生中,选绘画课人数占比为14. 一列单项式按以下规律排列: , 则第2024个单项式是( )A、 B、 C、 D、15. 估计的值是在( )A、1到2之间 B、2到3之间 C、3到4之间 D、4到5之间二、填空题(本大题共4个小题,每小题2分,满分8分)
-
16. 因式分解: .17. 如图,已知 , 请添加一个条件 , 使得 .
 18. 小丽某周每天的睡眠时间如下(单位:h):8,10,9,8,9,11,9则这组数据的众数是 .19. 如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若母线长l为 , 扇形的圆心角为 , 则圆锥的底面半径r为 .
18. 小丽某周每天的睡眠时间如下(单位:h):8,10,9,8,9,11,9则这组数据的众数是 .19. 如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若母线长l为 , 扇形的圆心角为 , 则圆锥的底面半径r为 .
三、解答题
-
20. 计算:21. 如图 , , , 求证: .
 22. 某学校为鼓励学生积极参加体育锻炼,派王老师和李老师去购买一些篮球和排球.回校后,王老师和李老师编写了一道题:
22. 某学校为鼓励学生积极参加体育锻炼,派王老师和李老师去购买一些篮球和排球.回校后,王老师和李老师编写了一道题:
同学们,请求出篮球和排球的单价各是多少元?
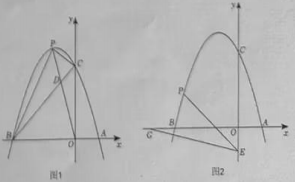
23. 非物质文化遗产是中华民族古老生命记忆和活态的文化基因,文山州非物质文化遗产资源丰富,品类繁多,文山市第三中学为让学生深入了解非物质文化遗产,决定邀请A铜鼓舞,B壮剧,C坡芽情歌,D葫芦笙舞制作的相关传承人(每项一人)进校园宣讲.(1)、若从以上非物质遗产中任选一个,则选中C坡芽情歌传承人的概率是 .(2)、若该学校决定邀请两位非遗传承人进校园宣讲,请用画树状图或列表的方法,求选中B壮剧和D葫芦笙舞制作传承人的概率.24. 2024年中考越来越近,班主任李老师打算在中考结束当天送班上每个同学一束花,李老师打算去花店购买向日葵和香槟玫瑰组合的鲜花.已知买2支向日葵和1支香槟玫瑰共需花费14元,3支香槟玫瑰的价格比2支向日葵的价格多2元.(1)、求买一支向日葵和一支香槟玫瑰各需多少元?(2)、李老师准备每束花需向日葵和香槟玫瑰共15支,且向日葵的数量不少于6支,班上总共40个学生,设购买所有的鲜花所需费用为元,每束花有香槟玫瑰支,求与之间的函数关系式,并设计一种使费用最少的买花方案,并写出最少费用.25. 如图,在平行四边形中, , 过点作交的延长线于点 , 连接交于点 .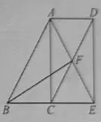 (1)、求证:四边形是矩形;(2)、连接 , 若 , , 求的长.
(1)、求证:四边形是矩形;(2)、连接 , 若 , , 求的长.