贵州省黔东南州2023-2024年八年级下学期数学期中考试模拟试卷
试卷更新日期:2024-04-17 类型:期中考试
一、选择题(本题共12小题,每题3分,共计36分)
-
1. 的倒数是( )A、 B、 C、 D、2. 在中, , , , 则以AB为边的正方形的周长是( )A、12 B、16 C、20 D、253. 如图,平行四边形中,已知 , 则的值是( )
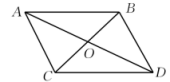 A、8 B、12 C、6 D、4. 下列曲线中不能表示是的函数的是( )A、
A、8 B、12 C、6 D、4. 下列曲线中不能表示是的函数的是( )A、 B、
B、 C、
C、 D、
D、 5. 若 , 则x的值可以是( )A、 B、 C、1 D、26. 如图,直线l上有三个正方形a,b,c,若a,c的面积分别为6和8,则b的面积为( )
5. 若 , 则x的值可以是( )A、 B、 C、1 D、26. 如图,直线l上有三个正方形a,b,c,若a,c的面积分别为6和8,则b的面积为( ) A、6 B、8 C、10 D、147. 如图,在中,的平分线交于点 , 若 , , 则的长( )
A、6 B、8 C、10 D、147. 如图,在中,的平分线交于点 , 若 , , 则的长( ) A、1 B、1.5 C、2 D、38. 如图1,中,点P从点C出发,匀速沿向点A运动,连接 , 设点P的运动距离为x , 的长为y , y关于x的函数图象如图2所示,则当点P为中点时,的长为( )
A、1 B、1.5 C、2 D、38. 如图1,中,点P从点C出发,匀速沿向点A运动,连接 , 设点P的运动距离为x , 的长为y , y关于x的函数图象如图2所示,则当点P为中点时,的长为( )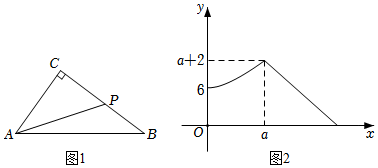 A、5 B、8 C、 D、9. 化简的结果为( )A、 B、 C、 D、10. 如图,已知中,的垂直平分线交于点 , 的垂直平分线交于点 , 点为垂足, , , , 则( )
A、5 B、8 C、 D、9. 化简的结果为( )A、 B、 C、 D、10. 如图,已知中,的垂直平分线交于点 , 的垂直平分线交于点 , 点为垂足, , , , 则( ) A、 B、 C、 D、11. 如图,矩形中, , , 点P为平面内一点,且 , 点Q为CD上一个动点,则的最小值为( )
A、 B、 C、 D、11. 如图,矩形中, , , 点P为平面内一点,且 , 点Q为CD上一个动点,则的最小值为( ) A、11 B、 C、 D、1312. 如图1,在中, , 于点 . 动点从点出发,沿折线方向运动,运动到点停止.设点的运动路程为 , 的面积为 , 与的函数图象如图2,则的长为( )
A、11 B、 C、 D、1312. 如图1,在中, , 于点 . 动点从点出发,沿折线方向运动,运动到点停止.设点的运动路程为 , 的面积为 , 与的函数图象如图2,则的长为( ) A、6 B、8 C、10 D、13
A、6 B、8 C、10 D、13二、填空题(本题共有4小题,每空4分,共计16分)
-
13. 若要使有意义,则x的取值范围为 .14. 如图,在平面直角坐标系中,点 , 的坐标分别为 , . 以点为圆心,以为半径画弧交轴正半轴于点 , 则点的坐标为 .
 15. 如图,在平面直角坐标系中,E是的中点,已知 , , , , 点P是线段上的一个动点,当的长为时,以点P , A , D , E为顶点的四边形是平行四边形.
15. 如图,在平面直角坐标系中,E是的中点,已知 , , , , 点P是线段上的一个动点,当的长为时,以点P , A , D , E为顶点的四边形是平行四边形. 16. 将正方形 …按如图所示的方式放置,点和点 分别在直线和 x轴上,已知点 , , 则 的坐标是 .
16. 将正方形 …按如图所示的方式放置,点和点 分别在直线和 x轴上,已知点 , , 则 的坐标是 .
三、解答题(本题共有9个小题,17、18题每道题8分,19题10分,其余12分,共计98分)
-
17. 计算: .18. 先化简,再求值: , 其中.19. 如图,在中, , , , 的垂直平分线交于点 , 交于点 , 求的长.
 20. 如图,的对角线 , 相交于点 , 点 , 分别是线段 , 的中点,若 , 的周长是 . 求:
20. 如图,的对角线 , 相交于点 , 点 , 分别是线段 , 的中点,若 , 的周长是 . 求: (1)、的长度;(2)、的长度.21. 如图,直线:与直线:交于点E .
(1)、的长度;(2)、的长度.21. 如图,直线:与直线:交于点E . (1)、求A , D , E点坐标;(2)、求四边形的面积;22. 观察以下式子的化简过程:
(1)、求A , D , E点坐标;(2)、求四边形的面积;22. 观察以下式子的化简过程:① ,
② ,
③ ,
④ ,
……
根据以上式子的化简过程,得出规律.完成下列问题:
(1)、如果n为正整数,那么的值为;(2)、根据以上规律计算:的值.23. 某小区在创文工作中,在临街的拐角清理出了一块可以绿化的空地,如图,通过测量得到 , , , , . (1)、求、两点之间的距离;(2)、若平均每平方米空地的绿化费用为150元,试计算绿化这片空地共需花费多少元?24. 某校甲、乙两班参加植树活动.乙班先植树20棵,然后甲班才开始与乙班一起植树.设甲班植树的总量为(棵),乙班植树的总量为(棵),两班一起植树所用的时间(从甲班开始植树时计时)为x(时),分别与x之间的部分函数图象如图所示.
(1)、求、两点之间的距离;(2)、若平均每平方米空地的绿化费用为150元,试计算绿化这片空地共需花费多少元?24. 某校甲、乙两班参加植树活动.乙班先植树20棵,然后甲班才开始与乙班一起植树.设甲班植树的总量为(棵),乙班植树的总量为(棵),两班一起植树所用的时间(从甲班开始植树时计时)为x(时),分别与x之间的部分函数图象如图所示. (1)、当时,分别求与x之间的函数关系式.(2)、如果甲、乙两班均保持前4个小时的工作效率,通过计算说明,当时,甲、乙两班植树的总量之和能否超过180棵.25. 阅读下面材料:
(1)、当时,分别求与x之间的函数关系式.(2)、如果甲、乙两班均保持前4个小时的工作效率,通过计算说明,当时,甲、乙两班植树的总量之和能否超过180棵.25. 阅读下面材料:
小明遇到这样一个问题:如图①,在中, , 且 , 试求的值.
(1)、小明发现,过点E作 , 交的延长线于点F , 经过推理得到 , 再计算就能够使问题得到(1)解决(如图②),并写出推理和计算过程.(2)、参考小明思考问题的方法,请你解决如下问题:如图③,已知和矩形 , 与交于点G , 求的度数.