贵州省安顺市2024年中考数学一模考试试卷

试卷更新日期：2024-04-17 类型：中考模拟

进入出卷网下载

一、选择题：本题共12小题，每小题3分，共36分。在每小题给出的选项中，只有一项是符合题目要求的。

1. 当前，手机移动支付已经成为新型的消费方式，中国正在向无现金支付发展 $.$ 小明在妈妈的微信零钱明细中看到，收入 $200$ 元被记作 $+ 200$ 元，则 $- 35$ 元表示( )

A、收入 $35$ 元 B、支出 $35$ 元 C、收入 $165$ 元 D、支出 $165$ 元

查看试题解析
2. 中国航天取得了举世瞩目的成就，为人类和平贡献了中国智慧和中国力量，下列是有关中国航天的图标，其文字上方的图案是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 随着“村超”和“村 $B A$ ”成为贵州响当当的名片，带动贵州旅游业火爆出圈、走向全国 $. 2024$ 年龙年春节期间，旅游成为“新年俗”，贵州省累计接待国内游客约 $2502$ 万人次， $2502$ 万用科学记数法可表示为( )

A、 $2502 \times 10^{4}$ B、 $2.502 \times 10^{6}$ C、 $2.502 \times 10^{7}$ D、 $25.02 \times 10^{6}$

查看试题解析
4. 如图，四个大小相同的正方体搭成的几何体，从正面看得到的图形是（　　）

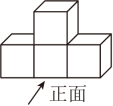A、 B、 C、 D、

查看试题解析
5. 下列运算正确的是( )

A、 $x^{2} \cdot x^{3} = x^{6}$ B、 $x^{3} \div x^{2} = x$ C、 $(x^{2})^{3} = x^{5}$ D、 $x^{2} + x^{3} = x^{5}$

查看试题解析
6. 一个等腰直角三角尺和一把直尺按如图所示的位置摆放，若 $∠ 1 = 20 °$ ，则∠2的度数是（）

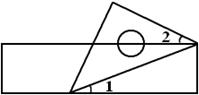A、15° B、20° C、25° D、40°

查看试题解析
7. “八年级数学课本共 $160$ 页，某同学随手翻开，恰好翻到第 $60$ 页”，这个事件是( )

A、必然事件 B、不可能事件 C、随机事件 D、以上都不正确

查看试题解析
8. 关于 $x$ 的方程 $x^{2} - m x - 3 = 0$ 的根的情况是( )

A、有两个不相等的实数根 B、有两个相等的实数根
C、没有实数根 D、不能确定

查看试题解析
9. 如图，电路图有4只未闭合的开关，一个电源和一个小灯泡，已知电路图上的每个部分都能正常工作，任意闭合其中两只开关，使得小灯泡发光的概率为（）

A、 $\frac{5}{6}$ B、 $\frac{9}{12}$ C、 $\frac{1}{2}$ D、 $\frac{3}{4}$

查看试题解析
10. 如图，在 $△ A B C$ 中， $∠ A = 30 °$ ， $∠ A C B = 90 °$ ， $B C = 4$ ，以点 $A$ 为圆心， $A C$ 长为半径画弧，交 $A B$ 于点 $D$ ，则图中阴影部分的面积是( )

A、 $8 \sqrt{3} - 4 π$ B、 $8 \sqrt{3} - 2 π$ C、 $16 \sqrt{3} - 8 π$ D、 $16 \sqrt{3} - 4 π$

查看试题解析
11. 如图，在△ABC中，BC＝6，AC＝8，∠C＝90°，以点B为圆心，BC长为半径画弧，与AB交于点D，再分别以A、D为圆心，大于 $\frac{1}{2}$ AD的长为半径画弧，两弧交于点M、N，作直线MN，分别交AC、AB于点E、F，则AE的长度为（）

A、 $\frac{5}{2}$ B、3 C、2 $\sqrt{2}$ D、 $\frac{10}{3}$

查看试题解析
12. 如图， $A C$ 为矩形 $A B C D$ 的对角线，已知 $A D = 3$ ， $C D = 4$ ，点 $P$ 沿折线 $C - A - D$ 以每秒 $1$ 个单位长度的速度运动 $($ 运动到 $D$ 点停止 $)$ ，过点 $P$ 作 $P E ⊥ B C$ 于点 $E$ ，则 $△ C P E$ 的面积 $y$ 与点 $P$ 运动的路程 $x$ 间的函数图象大致是( )

A、 B、 C、 D、

查看试题解析

二、填空题：本题共4小题，每小题4分，共16分。

13. 分解因式： $y^{2} - 1 =$ ．

查看试题解析
14. 若一个正多边形的一个内角是 $140 °$ ，则这个多边形的边数为．

查看试题解析
15. 如图，程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”，执行该程序框图，如果输出m的值为5，那么输入x的值为．

查看试题解析
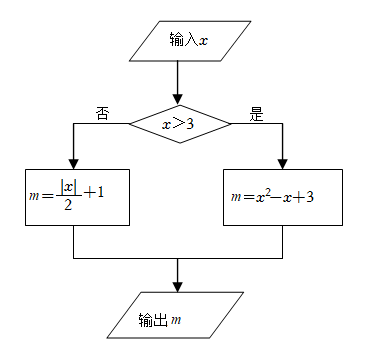16. 在边长为4的正方形ABCD中，点E在AB边上，点N在AD边上，点M为BC中点，连接DE、MN、BN，若DE＝MN，cos∠AED＝ $\frac{\sqrt{17}}{17}$ ，则BN的长为．

查看试题解析

三、解答题：本题共8小题，共88分。解答应写出文字说明，证明过程或演算步骤。

17.

(1)、解不等式组： $\{\begin{array}{l} x - 3 (x - 2) \leq 4 \\ \frac{1 + 2 x}{3} > x - 1 \end{array}$ ；

(2)、小红同学在化简的过程中出现了错误，请根据她的解答过程，回答问题：
化简： $x + 2 - \frac{x (x + 4)}{x + 2}$
解：原式 $= (x + 2) (x + 2) - x (x + 4)$ 第一步
$= (x^{2} + 4 x + 4) - (x^{2} + 4 x)$ 第二步
$= 4$ 第三步
$①$ 小红同学的解答从第步出错的；
$②$ 请写出正确的化简过程．

查看试题解析
18. 如图，平行四边形 $A B C D$ 中， $A C ⊥ B C$ ，过点 $D$ 作 $D E / / A C$ 交 $B C$ 的延长线于点 $E$ ，点 $M$ 为 $A B$ 的中点，连接 $C M$ ．

(1)、求证：四边形 $A D E C$ 是矩形；

(2)、若 $C M = 6.5$ ，且 $A C = 12$ ，求四边形 $A D E B$ 的面积．

查看试题解析
19. 随着人们“节能环保，绿色出行”意识的增强，越来越多的人喜欢骑自行车出行，也给自行车商家带来商机．某自行车行经营的A型自行车去年销售总额为8万元．今年该型自行车每辆售价预计比去年降低200元．若该型车的销售数量与去年相同，那么今年的销售总额将比去年减少10%，求：

(1)、A型自行车去年每辆售价多少元？

(2)、该车行今年计划新进一批A型车和新款B型车共60辆，且B型车的进货数量不超过A型车数量的两倍．已知，A型车和B型车的进货价格分别为1500元和1800元，计划B型车销售价格为2400元，应如何组织进货才能使这批自行车销售获利最多？

查看试题解析
20. 探究函数性质时，我们经历了列表、描点、连线画函数图象，观察分析图象特征，概括函数性质的过程 $.$ 以下是我们研究函数 $y = x + | - 2 x + 6 | + m$ 性质及其应用的部分过程，请按要求完成下列各小题．

$x$

$\dots$

$- 2$

$- 1$

$0$

$1$

$2$

$3$

$4$

$5$

$\dots$

$y$

$\dots$

$6$

$5$

$4$

$a$

$2$

$1$

$b$

$7$

$\dots$

(1)、写出函数关系式中 $m$ 及表格中 $a$ ， $b$ 的值：
$m =$ ， $a =$ ， $b =$ ；

(2)、根据表格中的数据在所给的平面直角坐标系中画出该函数的图象，并根据图象写出该函数的一条性质：；

(3)、已知函数 $y = \frac{16}{x}$ 的图象如图所示，结合你所画的函数图象，直接写出不等式 $x + | - 2 x + 6 | + m > \frac{16}{x}$ 的解集．

查看试题解析
21. 为建设美好公园社区，增强民众生活幸福感，如图 $1$ ，某社区服务中心在文化活动室墙外安装遮阳篷，便于社区居民休憩 $.$ 在如图 $2$ 的侧面示意图中，遮阳篷靠墙端离地高记为 $B C$ ，遮阳篷 $A B$ 长为 $5$ 米，与水平面的夹角为 $16 °$ ．

(1)、求点 $A$ 到墙面 $B C$ 的距离；

(2)、当太阳光线 $A D$ 与地面 $C E$ 的夹角为 $45 °$ 时，量得影长 $C D$ 为 $1.8$ 米，求遮阳篷靠墙端离地高 $B C$ 的长 $. ($ 结果精确到 $0.1$ 米；参考数据： $s i n 16 ° \approx 0.28$ ， $c o s 16 ° \approx 0.96$ ， $t a n 16 ° \approx 0.29)$

查看试题解析
22. 如图 $1$ ，已知 $R t △ A B C$ 中， $∠ A C B = 90 °$ ， $A B = 10$ ， $B C = m$ ，点 $D$ 在 $A C$ 上，连接 $B D$ ，作 $C E ⊥ A B$ ，交 $△ B D C$ 的外接圆 $⊙ O$ 于点 $E$ ，连结 $D E$ 和 $B E$ ．

(1)、求证： $∠ B D E = ∠ A$ ；

(2)、如图 $2$ ，若点 $D$ 是 $A C$ 中点，当 $m = 6$ 时，求 $B E$ 的长．

查看试题解析
23. 学校操场上有部分同学在玩丢沙包游戏，佳佳通过游戏得到启发编制了一道数学题，如图，在平面直角坐标系中，一个单位长度代表 $1$ 米长，佳佳在点 $A (6,1)$ 处将沙包 $($ 看成点 $)$ 抛出，其运动路线为抛物线 $C_{1}$ ： $y = a (x - 3)^{2} + 2$ 的一部分，亮亮恰在点 $B (0, m)$ 处接住，然后跳起将沙包回传，其运动路线为抛物线 $C_{2}$ ： $y = - \frac{1}{8} x^{2} + \frac{n}{8} x + m + 1$ 的一部分．

(1)、求抛物线 $C_{1}$ 的函数解析式：

(2)、若佳佳向前跑 $1$ 米，再竖直向上跳 $0.5$ 米，刚好接到沙包，求出此时 $n$ 的值；

(3)、若佳佳发现在 $x$ 轴上方 $1$ 米的高度上，且到点 $A$ 水平距离不超过 $1$ 米的范围内可以接到沙包，请直接写出符合条件的 $n$ 的取值范围．

查看试题解析
24. 综合与实践
新定义：我们把两个面积相等但不全等的三角形叫做积等三角形.

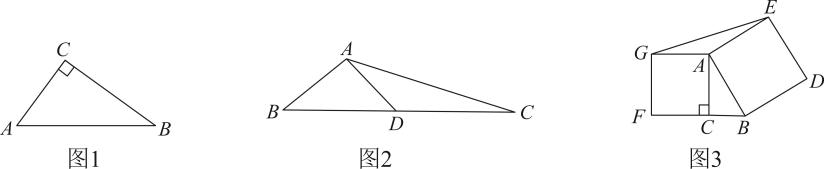(1)、【初步尝试】如图1，已知 $R t △ A B C$ 中， $∠ C = 90 °$ ， $A B = 5$ ， $B C = 4$ ， P为 $A C$ 上一点，当AP=时， $△ A B P$ 与 $△ C B P$ 为积等三角形；

(2)、【理解运用】如图2， $△ A B D$ 与 $△ A C D$ 为积等三角形；若 $A B = 3$ ， $A C = 5$ ，且线段 $A D$ 的长度为正整数，求 $A D$ 的长；

(3)、【综合应用】如图3，已知 $R t △ A B C$ 中， $∠ A C B = 90 °$ ，分别以 $A C$ ， $A B$ 为边向外作正方形 $A B D E$ 和正方形 $A C F G$ ，连接 $E G$ ，求证： $△ A E G$ 与 $△ A B C$ 为积等三角形.

查看试题解析

$x$	$\dots$	$- 2$	$- 1$	$0$	$1$	$2$	$3$	$4$	$5$	$\dots$
$y$	$\dots$	$6$	$5$	$4$	$a$	$2$	$1$	$b$	$7$	$\dots$