贵州省2024年中考导向权威预测数学模拟预测题
试卷更新日期:2024-04-17 类型:中考模拟
一、选择题:以下每小题均有A、B、C、D四个选项,其中只有一个选项正确,请用2B铅笔在答题卡相应位置作答,每小题3分,共36分.
-
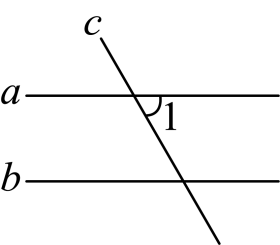
1. 的倒数是( )A、 B、 C、5 D、2. 如图,是两条平行直线和被直线所截形成的角,图中和相等的角有几个( )
 A、1个 B、2个 C、3个 D、4个3. 对于:① , ② , ③ , ④从左到右的计算,正确的是( )A、①② B、①③ C、②③ D、③④4. 如图所示的长方体的截面是( )
A、1个 B、2个 C、3个 D、4个3. 对于:① , ② , ③ , ④从左到右的计算,正确的是( )A、①② B、①③ C、②③ D、③④4. 如图所示的长方体的截面是( )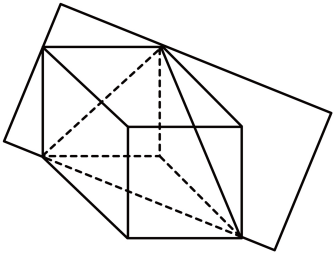 A、长方形 B、正方形 C、三角形 D、三棱柱5. 贵州榕江县位于贵州省东南部,是一个自然风光秀丽、民族文化丰富多彩的地方,据调查,榕江县在2023年的常住人口为29万人,数据29万用科学记数法表示为( )A、 B、 C、 D、6. 小明和小张周末与家人驾车去游玩,已知他们的时间和行驶的路程的关系如图所示,下列说法错误的是( )
A、长方形 B、正方形 C、三角形 D、三棱柱5. 贵州榕江县位于贵州省东南部,是一个自然风光秀丽、民族文化丰富多彩的地方,据调查,榕江县在2023年的常住人口为29万人,数据29万用科学记数法表示为( )A、 B、 C、 D、6. 小明和小张周末与家人驾车去游玩,已知他们的时间和行驶的路程的关系如图所示,下列说法错误的是( ) A、小明家的行驶路程与时间的关系为 B、小张家的行驶路程与时间的关系为 C、小明家的行驶速度更快 D、小张家的行驶速度更快7. 一大货车拉货从城到城,途中货物的数量有所变化,其路程与时间的关系图象如图所示,下列说法正确的是( )
A、小明家的行驶路程与时间的关系为 B、小张家的行驶路程与时间的关系为 C、小明家的行驶速度更快 D、小张家的行驶速度更快7. 一大货车拉货从城到城,途中货物的数量有所变化,其路程与时间的关系图象如图所示,下列说法正确的是( ) A、货车在时的速度大于时的速度 B、从图中不能看出两城的距离 C、货车在前拉的货物的数量多于后拉的货物的数量 D、货车在前拉的货物的数量少于后拉的货物的数量8. 已知一次函数的图象与正比例函数的图象经过点 , 则该一次函数函数的图象与坐标轴围成的三角形的面积为( )A、1 B、 C、2 D、9. 在一个黑色盒子里有1个白球,现在放入若干个黑球,它们与白球除了颜色外都相同,搅匀后从中任意摸出两个球,使得(摸出一白一黑)(摸出两黑),则放入的黑球个数为( )A、3 B、4 C、5 D、610. 如图,正方形内接于圆 , 连接 , , 其交点刚好经过圆心,若 , 则阴影部分面积为( )
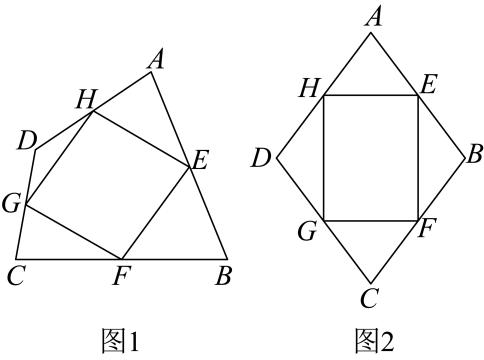
A、货车在时的速度大于时的速度 B、从图中不能看出两城的距离 C、货车在前拉的货物的数量多于后拉的货物的数量 D、货车在前拉的货物的数量少于后拉的货物的数量8. 已知一次函数的图象与正比例函数的图象经过点 , 则该一次函数函数的图象与坐标轴围成的三角形的面积为( )A、1 B、 C、2 D、9. 在一个黑色盒子里有1个白球,现在放入若干个黑球,它们与白球除了颜色外都相同,搅匀后从中任意摸出两个球,使得(摸出一白一黑)(摸出两黑),则放入的黑球个数为( )A、3 B、4 C、5 D、610. 如图,正方形内接于圆 , 连接 , , 其交点刚好经过圆心,若 , 则阴影部分面积为( )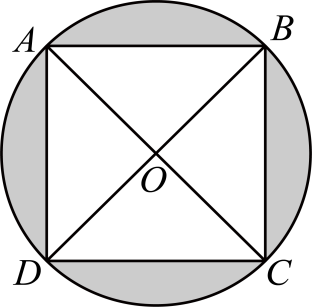 A、 B、 C、 D、11. 意大利著名画家达·芬奇用如图所示的方法证明了勾股定理,图2是将图1沿直线剪开,将右半部分上下翻转得到的图形,其中四边形 , 四边形与四边形均为正方形,若图1中空白部分面积为37,线段的长为7,则图2中两个直角三角形的面积和为( )
A、 B、 C、 D、11. 意大利著名画家达·芬奇用如图所示的方法证明了勾股定理,图2是将图1沿直线剪开,将右半部分上下翻转得到的图形,其中四边形 , 四边形与四边形均为正方形,若图1中空白部分面积为37,线段的长为7,则图2中两个直角三角形的面积和为( ) A、6 B、12 C、15 D、2512. 如图,以的顶点为圆心作一个圆,与相交于点 , 与相切于点 , 与相交于点 , 点是优弧的一点,连接与 , 若的半径为3, , , 则的度数是( )
A、6 B、12 C、15 D、2512. 如图,以的顶点为圆心作一个圆,与相交于点 , 与相切于点 , 与相交于点 , 点是优弧的一点,连接与 , 若的半径为3, , , 则的度数是( )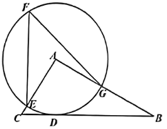 A、 B、 C、 D、
A、 B、 C、 D、二、填空题:每小题4分,共16分.
-
13. 要使分式有意义,则的取值范围是.14. 2023年,贵州环雷公山马拉松比赛圆满落幕,马拉松男子组前十名的成绩如下,统计时以2分30秒为标准,超出部分记为正,不足部分记为负,记录如下(单位:秒):
排名
1
2
3
4
5
6
7
8
9
10
用时
0
在最终的成绩中,用时的中位数是 , 实际平均用时为.
15. 如图,在平面直角坐标系中,点 , , 的坐标分别为 , , , 点是三角形的外接圆上一点,交线段于点 , 若 , 则点的坐标为. 16. 如图,在中, , , , 平分 , 点F是的中点,点E是上的动点,则的最小值为 .
16. 如图,在中, , , , 平分 , 点F是的中点,点E是上的动点,则的最小值为 .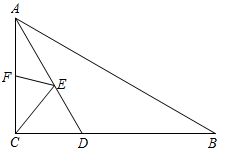
三、解答题:本大题9小题,共98分.解答应写出必要的文字说明、证明过程或演算步骤.
-
17.(1)、若 , , 请求出的值;(2)、化简: .18. 在全国开始大力宣传垃圾分类至今,绝大部分的公民都参与其中,小明同学就一个社区的居民对垃圾分类的了解程度做了调查,在调查的过程当中发现,大多数青年人都会自觉遵守垃圾分类,将每种垃圾分的清清楚楚,而一些中老年人却没有十分关注这一活动,大多数学生可以分清可回收垃圾和厨余垃圾,但并不是十分了解其他垃圾和有毒有害垃圾,下面是此次调查的情况,并将调查结果制成了如下的统计图表,其中代表十分了解,代表比较了解,代表一般了解,代表了解一些,代表完全不了解.

根据以上统计图表回答下列问题:
(1)、此次参与调查的人数总数是人;(2)、若该社区总计有2000人,请你估计比较了解的大概有多少人;(3)、据统计,2023年我国产生的可回收垃圾约为0.5亿吨,所创造的经济总价值约为1000亿元,若要持续提升垃圾的回收利用价值,请根据此次调查结果给出一条合理的建议.19. 如图,在一个正六边形中,点是该正六边形的中心,将该六边形的每条边延长,延长线的交点分别为、、、、、 .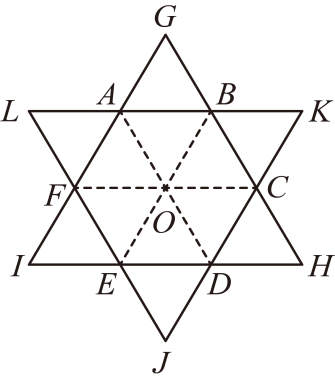 (1)、证明四边形是菱形;(2)、若的长为6,请计算正六边形的面积.20. 君子是我国古代对有德者的美称,梅兰竹菊俗称四君子,因为它们不畏风寒,像堂堂君子一样,所以称它们为四君子.梅花雪中来,箭兰幽谷藏,竹林风中立,明菊飘淡香.为装饰校园,某学校计划购入一批《梅》《兰》《竹》《菊》的国画,已知《梅》和《菊》的价格相同,《兰》和《竹》的价格相同,每幅《梅》比《兰》贵15元,并且用1200元购买《菊》和用900元购买《竹》的数量相同.(1)、求每幅《梅》《兰》《竹》《菊》的价格分别为多少元;(2)、该学校计划购买《梅》和《兰》共60幅,总费用不超过3120元,那么该学校最多能购买多少幅《梅》?21. 某天早晨小明在去图书馆的途中看到了一棵大树 , 而他正好站在大树影子的顶点上,他想起了之前在某一本书上看到的古人辨别方位的方法,他也想尝试,在等待15分钟之后,大树的影子由变为了 , 由此他确定了方位,如图所示,测得长度为3米,长度为4米,且线段刚好在南北方向上,在东西方向,已知在点处大树顶端的仰角为 , 求大树的高度,结果精确到0.1米, , , .
(1)、证明四边形是菱形;(2)、若的长为6,请计算正六边形的面积.20. 君子是我国古代对有德者的美称,梅兰竹菊俗称四君子,因为它们不畏风寒,像堂堂君子一样,所以称它们为四君子.梅花雪中来,箭兰幽谷藏,竹林风中立,明菊飘淡香.为装饰校园,某学校计划购入一批《梅》《兰》《竹》《菊》的国画,已知《梅》和《菊》的价格相同,《兰》和《竹》的价格相同,每幅《梅》比《兰》贵15元,并且用1200元购买《菊》和用900元购买《竹》的数量相同.(1)、求每幅《梅》《兰》《竹》《菊》的价格分别为多少元;(2)、该学校计划购买《梅》和《兰》共60幅,总费用不超过3120元,那么该学校最多能购买多少幅《梅》?21. 某天早晨小明在去图书馆的途中看到了一棵大树 , 而他正好站在大树影子的顶点上,他想起了之前在某一本书上看到的古人辨别方位的方法,他也想尝试,在等待15分钟之后,大树的影子由变为了 , 由此他确定了方位,如图所示,测得长度为3米,长度为4米,且线段刚好在南北方向上,在东西方向,已知在点处大树顶端的仰角为 , 求大树的高度,结果精确到0.1米, , , . 22. 如图,在平面直角坐标系中,一次函数的图象经过点 , 且与二次函数的图象交于点 .
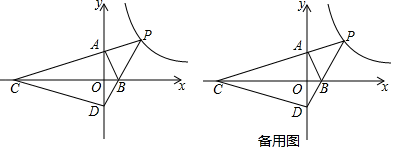
22. 如图,在平面直角坐标系中,一次函数的图象经过点 , 且与二次函数的图象交于点 .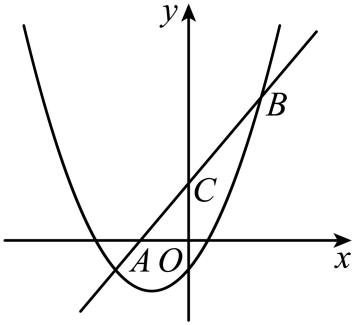 (1)、求一次函数与二次函数的表达式;(2)、设是直线上一点,过点作轴,交二次函数的图象于点 , 若以点、、、为顶点的四边形是平行四边形,求点的坐标.23. 如图, , 是上的两点,是的直径,过点的切线交的延长线于点 , , 连接 , , .
(1)、求一次函数与二次函数的表达式;(2)、设是直线上一点,过点作轴,交二次函数的图象于点 , 若以点、、、为顶点的四边形是平行四边形,求点的坐标.23. 如图, , 是上的两点,是的直径,过点的切线交的延长线于点 , , 连接 , , . (1)、求证∶;(2)、若 , , 求的半径;(3)、在(2)的条件下,求出的面积.
(1)、求证∶;(2)、若 , , 求的半径;(3)、在(2)的条件下,求出的面积.