贵州省黔东南州2024年初中学业水平第一次数学模拟试题

试卷更新日期：2024-04-17 类型：中考模拟

进入出卷网下载

一、选择题：以下每小题均有A、B、C、D四个选项，其中只有一个选项正确，请用HB或2B铅笔在《答题卡》上填涂正确选项的字母框，每小题3分，共36分．

1. 在实数-5， -2， 0， 3中，负数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
2. 观察下列图案，既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 在国家“一带一路”倡议下，我国与欧洲开通了互利互惠的中欧专列．行程最长，途经城市和国家最多的一趟专列全程长13000km，将 13000用科学记数法表示应为（）

A、 $1 ． 3 \times 10^{4}$ B、 $0 ． 13 \times 10^{5}$ C、 $1 ． 3 \times 10^{5}$ D、 $13 \times 10^{3}$

查看试题解析
4. 下列等式成立的是（）

A、 $a^{2} + a^{3} = a^{5}$ B、 $a \cdot a^{3} = a^{3}$ C、 $a^{6} \div a^{2} = a^{4}$ D、 $a^{2} - b^{2} = (a - b)^{2}$

查看试题解析
5. 小星记录了某地一周每天的最高气温，数据如下表所示：
星期
一
二
三
四
五
六
日
最高气温(℃)
23
25
24
22
25
24
25
则这组数据的中位数和众数分别是（）

A、22C°， 25C° B、25C°， 22C° C、24C°， 25C° D、25C°， 24C°

查看试题解析
6. 计算 $\frac{x}{x + 1} + \frac{1}{x + 1}$ 的结果是（）

A、 $\frac{x}{x + 1}$ B、 $\frac{1}{x + 1}$ C、-1 D、1

查看试题解析
7. 汽车油箱中有汽油20L，行驶的平均耗油量为0.1L/km，则汽车最多能行驶（）

A、100km B、200km C、300km D、400km

查看试题解析
8. 如图①是某商场某品牌的椅子，图②是其侧面图， $∠ D E F = 120 °,$ DE与地面平行，则 $∠ C A B$ 等于（）

A、70° B、65° C、 $60 °$ D、50°

查看试题解析
9. 如图，AB是 $⊙ O$ 的直径，C，D是 $⊙ O$ 上的两点，连接AC，CD，AD，若 $∠ A D C = 75 °$ ，则 $∠ B A C$ 的度数是（）

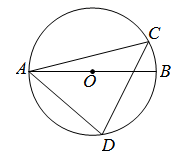A、15° B、25° C、30° D、75°

查看试题解析
10. 已知A(-1， a)， B(2， b)， C(3， c) 都在反比例函数 $y = \frac{k}{x}$ （k>0）的图象上，则a，b，c的大小关系是（）

A、b<a<c B、c<b<a C、a<b<c D、a<c<b

查看试题解析
11. 如图，在△ABC中， ∠C=90°，∠B=30°，按下列步骤尺规作图：①以A为圆心，适当长为半径画弧分别交AB、AC于点M和N；②分别以M、N为圆心，大于 $\frac{1}{2} M N$ 的长为半径画弧，两弧交于点P； ③连接AP 并延长交 BC于点 D．以下结论错误的是（）

A、AD是∠BAC的角平分线 B、∠ADC=60° C、点 D在线段AB的垂直平分线上 D、 $S_{A B D} : S_{A B C} = 1 : 2$

查看试题解析
12. 如图，已知A(1， y₁)、B(4， y₂)为反比例函数 $y = \frac{4}{x}$ （x>0）象上的两点，连接OA， OB， AB，则三角形OAB的面积是（）

A、4 B、 $\frac{9}{2}$ C、 $\frac{15}{4}$ D、 $\frac{15}{2}$

查看试题解析

二、填空题：每小题4分，共16分．

13. 计算： ${(\sqrt{4})}^{2} =$ ．

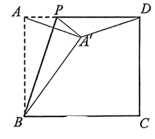
查看试题解析
14. 现从甲、乙、丙三名同学中，随机抽取一名同学参加学校举行的“学法用法知识竞赛”，则抽到乙的概率为．

查看试题解析
15. 分解因式： $a^{2} - 4$ .

查看试题解析
16. 如图，在矩形ABCD中， AB=3， AD=4，点P 是边AD上的一个动点(点P不与点A， D重合)，将△BAP沿BP折叠，使点A落在点A'的位置，连接AA'， DA'，若AA' = DA'，则AP 的长为．

查看试题解析

三、解答题(本大题共9题，共 98分．解答应写出必要的文字说明、证明过程或演算步骤)

17.

(1)、计算：

{(- 3)}^{2} + {(2024 - π)}^{0} - | - 4 |

(2)、下面是小明用配方法解一元二次方程

2 x^{2} + 4 x - 8 = 0

的过程，请认真阅读并完成相应的任务．

解：移项，得 $2 x^{2} + 4 x = 8$ 第一步

二次项系数化为1，得 $x^{2} + 2 x = 4$ 第二步

配方，得 $(x + 2)^{2} = 8$ 第三步

由此可得 $x + 2 = \pm 2 \sqrt{2}$ 第四步

所以， $x_{1} = - 2 + 2 \sqrt{2}, x_{2} = - 2 - 2 \sqrt{2}$ 第五步

①小明同学的解答过程，从第步开始出现错误；

②请写出你认为正确的解答过程．

查看试题解析

18. 如图，一次函数 $y_{1} = k_{1} x + b (k_{1} \neq 0)$ 的图象与反比例函数 $y_{2} = \frac{k_{2}}{x}$ 的图象交于点A(-4，-2)，B(2，m)．

(1)、求一次函数和反比例函数的表达式；

(2)、当x为何值时， $y_{1} < y_{2},$ 请直接写出x的取值范围．

查看试题解析
19. 某校文学社为了解学生课外阅读情况，对本校七年级的学生进行了课外阅读知识水平检测．为了解情况，从七年级学生中随机抽取部分女生和男生的测试成绩，将这些学生的成绩x(单位：分，0≤x≤100)分为5组：
A组：x<60， B组：60≤x<70， C组：70≤x<80， D组：80≤x<90， E组：90≤x≤100．
并提供了这5个组的如下4条信息：
①不完整的扇形统计图和条形图
②女生成绩在 70≤x<80的数据为：70， 72， 72， 72；
③男生成绩在 60≤x<80的数据为：72， 68， 62， 68， 70；
④抽取的男生和女生测试成绩的平均数、中位数、众数如表所示：

平均数
中位数
众数
男生测试成绩
76
a
68
女生测试成绩
76
72
b
请根据以上信息解答下列问题：

(1)、 a= ， b= ．

(2)、从七年级一共抽取了多少名学生?

(3)、在抽取的学生中，你认为男生测试成绩好还是女生测试成绩好? 并说明理由．

查看试题解析
20. 如图，在平行四边形ABCD中， E为DC边的中点，连接AE，若AE的延长线和BC的延长线相交于 F．

(1)、求证： AD=FC；

(2)、连接BE，若△AEB的面积为2，求平行四边形ABCD的面积．

查看试题解析

21. 2024年2月下旬，我省各地中小学陆续正常开学．开学之际，学生对书包的需求量增加．

市场调研：

某班数学兴趣小组对某商场进行调研后了解到如下信息：

信息一信息二

商场从厂家购进A、B两款书包，其中A款书包7个，B款书包5个，共付款920元，已知每个B款书包的进价比每个A款书包贵40元．

商场将B款书包按信息一中的进价提高50%后标价，实际销售时再打折出售，此时每个B款书包仍可获利35%．

问题解决：

(1)、每个A款书包的进价为元，每个B款书包的进价为元；

(2)、信息应用：

在信息二中，B款书包实际销售时打多少折出售?

查看试题解析

22. 随着传统能源的日益紧缺，太阳能的应用将会越来越广泛，如图①是一款太阳能路灯实物图，图②是某校兴趣小组测量太阳能路灯电池板距离地面高度的方案示意图，其中测角器的高 $C E = D F = 1 ． 5 m,$ 在点C处安置测角器，测得点A的仰角 $∠ A E G = 32 °,$ ，在与点C相距3.8m的点D处安置测角器，测得点A的仰角 $∠ A F G = 45 °$ (点C， D， B在同一条直线上) ．

(1)、设AB=xm，用含x的代数式表示BD的长；

(2)、求电池板距离地面的高度AB的长．
(结果精确到0.1m；参考数据： t $t a n 32 ° \approx 0 ． 62, s i n 32 ° \approx 0 ． 53, c o s 32 ° \approx 0 ． 85$ )

查看试题解析
23. 如图，⊙O是△ABC的外接圆，． $A B = A C,$ ，连接AO，延长AO交BC于点D，交⊙O于点E．

(1)、∠ACE的度数为度，写出图中一对全等的三角形：；

(2)、求证： △ADB∽△BDE；

(3)、若OD=DE，试求∠BAC的度数．

查看试题解析
24. 小明和小亮在做传球训练，某同学借做此情境编了一道数学题．
在如图的平面直角坐标系中，一个单位长度代表1m，小明从点A(8，2)处将球传出，其运动路线为抛物线 $C_{1} : y = a (x - 4)^{2} + 4$ 的一部分，小亮在 B处接住球，然后跳起将球传出，球的运动路线是抛物线 $C_{2} : y = - \frac{1}{10} x^{2} + \frac{n}{10} x + \frac{5}{2}$ 的一部分．

(1)、求抛物线C₁的函数表达式；

(2)、设抛物线C₁的顶点为点 M，在x轴上找一点P，求使| $| P A - P M |$ 的值最大的点P的坐标；

(3)、若小明在x轴上方2m的高度上，且到点A水平距离不超过1m的范围内可以接到球，求符合条件的n的整数值．

查看试题解析
25. 如图，在边长为2的正方形ABCD中，点E在CD边上，点F在BC边上，连接AE， DF，AE与DF相交于点 P．

(1)、【动手操作】在图1中画出线段AE， DF；

(2)、【问题探究】若 DF⊥AE．
①利用图2 探究 CE+CF的值；
②过点P作PM⊥CD， PN⊥BC，垂足分别为M， N，连接MN，试求MN的最小值．

查看试题解析

	平均数	中位数	众数
男生测试成绩	76	a	68
女生测试成绩	76	72	b

星期	一	二	三	四	五	六	日
最高气温(℃)	23	25	24	22	25	24	25