广东省惠州市惠城区2023-2024学年八年级下学期数学3月月考试卷

试卷更新日期：2024-04-17 类型：月考试卷

进入出卷网下载

一、选择题（本题共10个小题，每小题3分，共30分）

1. 化简 $\sqrt{20}$ 的结果是（）

A、 $5 \sqrt{2}$ B、 $2 \sqrt{10}$ C、 $2 \sqrt{5}$ D、 $4 \sqrt{5}$

查看试题解析
2. 下列各组数据为勾股数的是（）

A、7，24，25 B、2，3，4 C、 $\sqrt{3}$ ， $\sqrt{4}$ ， $\sqrt{5}$ D、1， $\sqrt{2}$ ， $\sqrt{3}$

查看试题解析
3. 下列根式中，与 $\sqrt{2}$ 是同类二次根式的是（）

A、 $\sqrt{24}$ B、 $\sqrt{\frac{3}{2}}$ C、 $\sqrt{12}$ D、 $\sqrt{18}$

查看试题解析
4. 下列运算正确的是（）

A、 $\sqrt{3} + \sqrt{3} = \sqrt{6}$ B、 $2 \sqrt{3} - \sqrt{3} = \sqrt{3}$ C、 $\sqrt{6} \times \sqrt{3} = \sqrt{9}$ D、 $\sqrt{4} \div \sqrt{2} = 2$

查看试题解析
5. 在直角坐标系中，已知点M的坐标为 $(7, 24)$ ，则点M到原点的距离是（）

A、7 B、24 C、25 D、31

查看试题解析
6. 小明想知道学校旗杆的高度，他发现旗杆上的绳子垂到地面还多了1米。当他把绳子的下端拉开5米后，发现下端刚好与接触地面，则旗杆的高度为（）。

A、11米 B、12米 C、13米． D、14米

查看试题解析
7. 平行四边形的一边长为 $8 c m$ ，周长为 $26 c m$ ，则这条边的邻边长是（）

A、 $18 c m$ B、 $16 c m$ C、 $10 c m$ D、 $5 c m$

查看试题解析
8. 如图，在下列给出的条件中，可以判定四边形ABCD为平行四边形的条件是（）

A、 $A D = B C$ ， $∠ B = ∠ D$ B、 $A D ∥ B C$ ， $A B = C D$ C、 $A B = C D$ ， $A D = B C$ D、 $A B ∥ C D$ ， $∠ A = ∠ B$

查看试题解析
9. 若 $△ A B C$ 的三边长a、b、c满足 $a^{2} + b^{2} + c^{2} = 6 a + 8 b + 10 c - 50$ ，那么 $△ A B C$ 是（）

A、等腰三角形 B、直角三角形 C、锐角三角形 D、钝角三角形

查看试题解析
10. 已知 $a + \frac{1}{a} = \sqrt{7}$ ，则 $a - \frac{1}{a} =$ （）

A、 $\sqrt{3}$ B、 $- \sqrt{3}$ C、 $\pm \sqrt{3}$ D、 $\pm \sqrt{11}$

查看试题解析

二、填空题（本题共6小题，每题3分，共18分）

11. 如果 $\sqrt{x + 8}$ 在实数范围内有意义，则x的取值范围是．

查看试题解析
12. 已知矩形的面积是 $4 \sqrt{3}$ ，其中一边长为 $\sqrt{6}$ ，则对角线长为．

查看试题解析
13. 如图，一棵大树（树干与地面垂直）在一次强台风中于离地面8米的B处折断倒下，倒下后的树顶C与树根A的距离为15米，则这棵大树在折断前的高度为米．

查看试题解析
14. 将边长为2的正方形OABC如图放置，O为原点．若∠α=15°，则点B的坐标为．

查看试题解析
15. 已知平行四边形的三个顶点的坐标分别为 $O (0, 0)$ 、 $A (2, 0)$ 、 $B (1, 1)$ ，则第四个顶点 $C$ 的坐标是．

查看试题解析
16. 如图是“赵爽弦图”，△ABH、△BCG、△CDF和△DAE是四个全等的直角三角形，四边形ABCD和EFGH都是正方形．如果AB=13，EF=7，那么AH等于。

查看试题解析

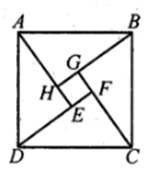
三、解答题（一）（本大题共4小题，17、18每题4分，19、20每题6分，共20分）

17. 已知 $b = \sqrt{a - 5} + \sqrt{5 - a} + 20$ ，求 $\sqrt{a + b}$ 的值．

查看试题解析
18. 计算： $\sqrt{36}$ ﹣ $\sqrt[3]{64} + \sqrt{(- 4)^{2}}$ ．

查看试题解析
19. 在Rt△ABC中，∠C=90°， $a$ ， b，c分别是∠A、∠B、∠C所对的三条边.

(1)、已知 $a = \sqrt{7}$ ， b=3，求c的长．

(2)、已知c=13，b=12，求 $a$ 的长．

查看试题解析
20. 如图，平行四边形 $A B C D$ 中，点E、F分别在 $A B 、 C D$ 上，且 $B E = D F$ ，求证： $A F = E C$ ．

查看试题解析

四、解答题（二）（本大题共3小题，21题8分，22、23每题10分，共28分）

21. 如图在四边形ABCD中，AB=BC=2，CD=3，DA=1，且∠B=90°，求∠DAB的度数．

查看试题解析
22. 在四边形ABCD中，已知AD∥BC，∠B＝∠D，AE⊥BC于点E，AF⊥CD于点F.

(1)、求证：四边形ABCD是平行四边形；

(2)、若AF＝2AE，BC＝6，求CD的长.

查看试题解析
23. 生活经验表明，靠墙摆放梯子时，若梯子底端离墙的距离约为梯子长度的 $\frac{1}{3}$ ，则梯子比较稳定，如图，AB为一长度为6米的梯子．

(1)、当梯子稳定摆放时，它的顶端能达到5.7米高的墙头吗？

(2)、如图2，若梯子底端向左滑动（3 $\sqrt{2}$ ﹣2）米，那么梯子顶端将下滑多少米？

查看试题解析

五、解答题（三）（本大题共2小题，24、25每题12分，共24分）

24. 问题背景：
在 $△ A B C$ 中， $A B$ 、 $B C$ 、 $A C$ 三边的长分别为 $\sqrt{5}$ ， $\sqrt{10}$ ， $\sqrt{13}$ ，求这个三角形的面积．
小辉同学在解答这道题时，先建立一个正方形网格（每个小正方形的边长为1），再在网格中画出格点 $△ A B C$ （即 $△ A B C$ 三个顶点都在小正方形的顶点处），如图1所示．这样不需求 $△ A B C$ 的高，而借用网格就能计算出它的面积．

(1)、请你直接写出 $△ A B C$ 的面积为；

(2)、思维拓展：
我们把上述求 $△ A B C$ 面积的方法叫做构图法．若 $△ A B C$ 三边的长分别为 $\sqrt{5}$ ， $2 \sqrt{2}$ ， $\sqrt{17}$ ，请利用图2的正方形网格（每个小正方形的边长为1）画出相应的 $△ A B C$ ，则它的面积是 ▲ ；

(3)、探索创新：
若 $△ A B C$ 三边的长分别为 $\sqrt{m^{2} + 16 n^{2}}$ ， $\sqrt{9 m^{2} + 4 n^{2}}$ ， $2 \sqrt{m^{2} + n^{2}}$ （m>0，n>0，且m≠n ，则这三角形的面积是．（用含 $m$ ， $n$ 的式子表示）

查看试题解析
25.

(1)、【问题探究】如图1，已知 $A D$ 是 $△ A B C$ 的中线，延长 $A D$ 至点E ，使 $D E ＝ A D$ ，连接 $B E$ ， $C E$ 可得四边形 $A B E C$ ，求证：四边形 $A B E C$ 是平行四边形．

(2)、【拓展提升】如图2，在 $△ A B C$ 的中线 $A D$ 上任取一点M（不与点A重合），过点M、点C分别作 $M E ∥ A B$ ， $C E ∥ A D$ ，连接 $A E$ ．求证：四边形 $A B M E$ 是平行四边形．

(3)、【灵活应用】如图3，在 $△ A B C$ 中， $∠ B = 90 °$ ， $A B = 4$ ， $B C = 6$ ，点D是 $B C$ 的中点，点M是直线 $A D$ 上的动点，且 $M E ∥ A B$ ， $C E ∥ A D$ ，当 $M E + M C$ 取最小值时，求线段 $C E$ 的长．

查看试题解析