湖北省武汉市2024年中考数学第二次模拟测试
试卷更新日期:2024-04-17 类型:中考模拟
一、选择题(本大题共10个小题,每小题3分,共30分.在每个小题给出的四个选项中,只有一项符合题目要求,请选出并在答题卡上将该项涂黑)
-
1. ﹣6的相反数是( )A、6 B、﹣6 C、 D、2. 第33届夏季奥运会将于2024年7月26日至8月11日在法国巴黎举行,如图所示巴黎奥运会项目图标中,轴对称图形是( )A、
 B、
B、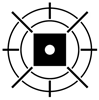 C、
C、 D、
D、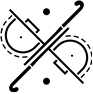 3. 下列事件中是必然事件的是( )A、打开电视机,正在播放《开学第一课》 B、任意画一个三角形,其内角和是180° C、经过有交通信号灯的路口,遇到红灯 D、买一张彩票,一定不会中奖4. 砚台与笔、墨、纸是中国传统的文房四宝,是中国书法的必备用具.如图是一方寓意“规矩方圆”的砚台,它的俯视图是( )
3. 下列事件中是必然事件的是( )A、打开电视机,正在播放《开学第一课》 B、任意画一个三角形,其内角和是180° C、经过有交通信号灯的路口,遇到红灯 D、买一张彩票,一定不会中奖4. 砚台与笔、墨、纸是中国传统的文房四宝,是中国书法的必备用具.如图是一方寓意“规矩方圆”的砚台,它的俯视图是( ) A、
A、 B、
B、 C、
C、 D、
D、 5. 下列运算正确的是( )A、2a6+a3=2a9 B、a2•a4=a8 C、(ab3)2=a2b6 D、(a+b)2=a2+b26. 如图,烧杯内液体表面与烧杯下底部平行,光线从液体中射向空气时发生折射,光线变成 , 点在射线上.已知 , , 则的度数为( )
5. 下列运算正确的是( )A、2a6+a3=2a9 B、a2•a4=a8 C、(ab3)2=a2b6 D、(a+b)2=a2+b26. 如图,烧杯内液体表面与烧杯下底部平行,光线从液体中射向空气时发生折射,光线变成 , 点在射线上.已知 , , 则的度数为( )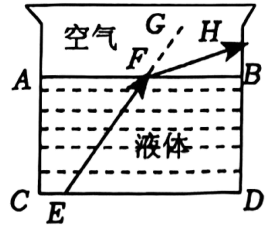 A、 B、 C、 D、7. 随着“双减”政策的实施和课后延时托管的开展,某学校开设了四门兴趣课程,分别为“绘画”“声乐”“陶艺”和“书法”.学校规定每人只能选择自己喜欢的一门课程学习.小明与小亮对这四门课程都感兴趣,在没有沟通的情况下,这两人选择同一门课程的概率是( )A、 B、 C、 D、8. 某烤鸭店在确定烤鸭的烤制时间时,主要依据的是表中的数据:
A、 B、 C、 D、7. 随着“双减”政策的实施和课后延时托管的开展,某学校开设了四门兴趣课程,分别为“绘画”“声乐”“陶艺”和“书法”.学校规定每人只能选择自己喜欢的一门课程学习.小明与小亮对这四门课程都感兴趣,在没有沟通的情况下,这两人选择同一门课程的概率是( )A、 B、 C、 D、8. 某烤鸭店在确定烤鸭的烤制时间时,主要依据的是表中的数据:鸭的质量/千克
0.5
1
1.5
2
2.5
3
3.5
4
烤制时间/分钟
40
60
80
100
120
140
160
180
设鸭的质量为x千克,烤制时间为t . 估计当x=3.8千克时,t的值约为( )
A、140 B、160 C、170 D、1809. 如图,在Rt△ABC中,∠ABC=40°,AB=6,斜边AB是半圆O的直径,点D是半圆上的一个动点,连接CD与AB交于点E , 若BE=BC时,弧BD的长为( )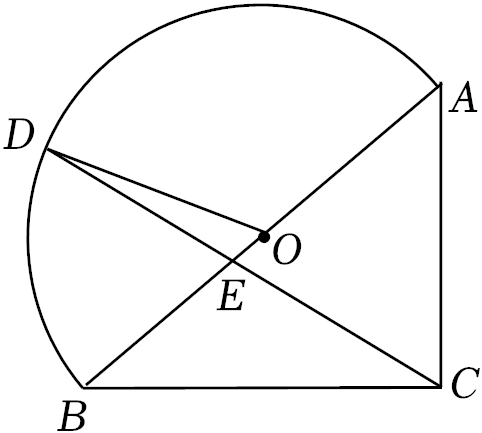 A、 B、 C、 D、10. 已知点(x1 , y1),(x2 , y2)在反比例函数(k为常数)图象上,x1≠x2 . 若x1•x2>0,则(x1﹣x2)(y1﹣y2)的值为( )A、0 B、非负数 C、正数 D、负数
A、 B、 C、 D、10. 已知点(x1 , y1),(x2 , y2)在反比例函数(k为常数)图象上,x1≠x2 . 若x1•x2>0,则(x1﹣x2)(y1﹣y2)的值为( )A、0 B、非负数 C、正数 D、负数二、填空题(本大题共6个小题,每小题3分,共18分)
-
11. 据中国青年报报道:“中央广播电视总台《2024年春节联欢晚会》为海内外受众奉上了一道除夕“文化大餐”.截至2月10日2时,总台春晚全媒体累计触达142亿人次,较去年增长29%,……”将数据142亿用科学记数法表示为: .12. 已知一次函数y=kx+b的图象过一、三象限,请写出符合上述条件的一个解析式: .13. 化简分式的结果是 .14. 图1是某种路灯的实物图片,图2是该路灯的平面示意图,MN为立柱的一部分,灯臂AC , 支架BC与立柱MN分别交于A , B两点,灯臂AC与支架BC交于点C , 已知∠MAC=60°,∠ACB=15°,AC=40cm , 则支架BC的长为cm . (结果精确到1cm , 参考数据:1.414,1.732,2.449)
 15. 在△ABC中,∠ACB=90°,AC=BC , 点D在△ABC内部,且满足∠ACD﹣∠BCD=2∠DAB , 若△BCD的面积为13,则CD= .
15. 在△ABC中,∠ACB=90°,AC=BC , 点D在△ABC内部,且满足∠ACD﹣∠BCD=2∠DAB , 若△BCD的面积为13,则CD= . 16. 已知抛物线y=ax2+bx+c(a , b , c为常数,a>0)经过A(﹣2,1),B(6,1)两点,下列四个结论:
16. 已知抛物线y=ax2+bx+c(a , b , c为常数,a>0)经过A(﹣2,1),B(6,1)两点,下列四个结论:①一元二次方程ax2+bx+c=0的根为x1=﹣2,x2=6;
②若点C(﹣5,y1)、D(π,y2)在该抛物线上,则y1>y2;
③对于任意实数t , 总有at2+bt≥4a+2b;
④对于a的每一个确定值(a>0),若一元二次方程ax2+bx+c=p(p为常数)有根,则p≥1﹣16a , 其中正确的结论是 . (填写序号)
三、解答题(本大题共8个小题,共72分.解答应写出文字说明,证明过程或演算步骤)
-
17. 解不等式组: , 并写出它的正整数解.18. 如图,已知E、F分别是▱ABCD的边BC、AD上的点,且 .
 (1)、求证:四边形AECF是平行四边形;(2)、若四边形AECF是菱形,且BC=10,∠BAC=90°,求BE的长.19. 为了解某校学生的身高情况,随机抽取该校男生、女生进行抽样调查.已知抽取的样本中,男生、女生的人数相同,利用所得数据绘制如下统计图表:
(1)、求证:四边形AECF是平行四边形;(2)、若四边形AECF是菱形,且BC=10,∠BAC=90°,求BE的长.19. 为了解某校学生的身高情况,随机抽取该校男生、女生进行抽样调查.已知抽取的样本中,男生、女生的人数相同,利用所得数据绘制如下统计图表:身高情况分组表
组别
A
B
C
D
E
身高(cm)
x<155
155≤x<160
160≤x<165
165≤x<170
x≥170
根据图表提供的信息,回答下列问题:
 (1)、抽取的样本中,男生的身高众数在 组,中位数在组;(2)、抽取的样本中,女生身高在E组的人数有多少人;(3)、已知该校共有男生840人,女生820人,请估计身高在C组的学生人数.20. 如图,AB为⊙O的直径,点C是AB上方⊙O上异于A , B的点,点D是的中点,过点D作DE∥AB交CB的延长线于点E , 连接AC , AD .
(1)、抽取的样本中,男生的身高众数在 组,中位数在组;(2)、抽取的样本中,女生身高在E组的人数有多少人;(3)、已知该校共有男生840人,女生820人,请估计身高在C组的学生人数.20. 如图,AB为⊙O的直径,点C是AB上方⊙O上异于A , B的点,点D是的中点,过点D作DE∥AB交CB的延长线于点E , 连接AC , AD .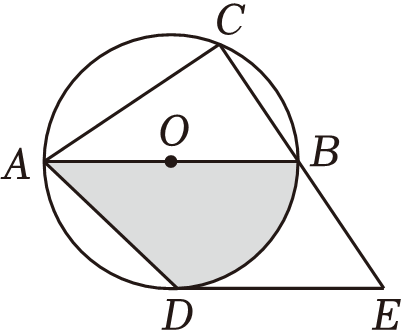 (1)、求证:DE是⊙O的切线;(2)、若AC=8,BC=6,求图中阴影部分的面积.21. 如图是由小正方形组成的7×7网格,每个小正方形的顶点叫做格点,点A , B , C均为格点.仅用无刻度的直尺在给定的网格中完成画图,画图过程用虚线,画图结果用实线.
(1)、求证:DE是⊙O的切线;(2)、若AC=8,BC=6,求图中阴影部分的面积.21. 如图是由小正方形组成的7×7网格,每个小正方形的顶点叫做格点,点A , B , C均为格点.仅用无刻度的直尺在给定的网格中完成画图,画图过程用虚线,画图结果用实线.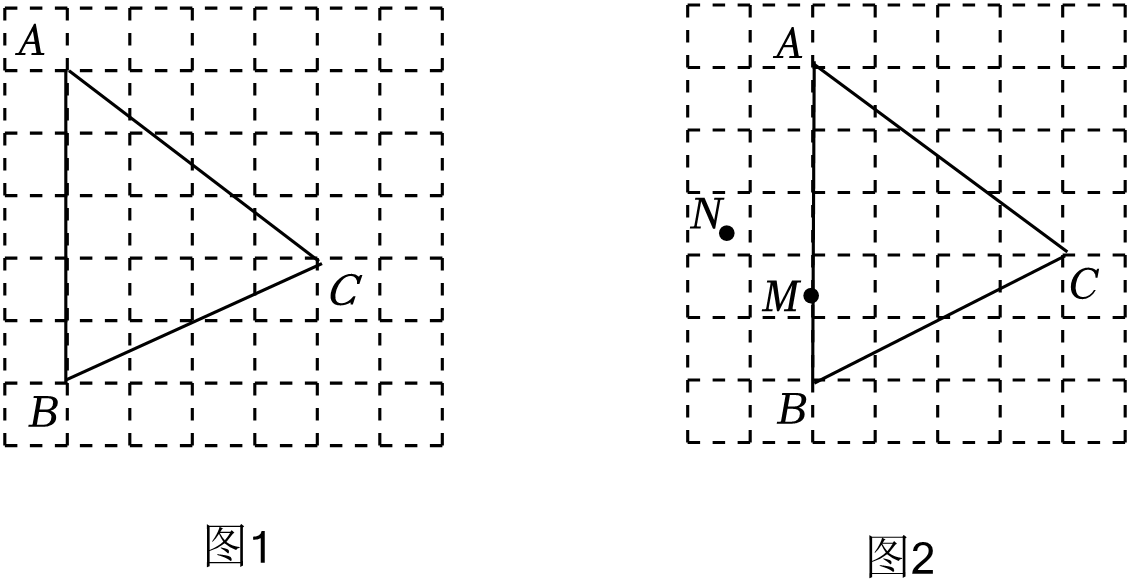 (1)、在图1中,先将线段CB绕点C顺时针旋转90°,画出旋转后的对应线段CE;再在线段CE上画点F , 连接BF , 使∠CFB=∠A;(2)、在图2中,M , N分别是网格线上和网格内的一点.先过点M画与BC平行的直线l;再在直线l上画一点P , 使NP⊥AB .22. 春回大地,万物复苏,又是一年花季到.某花圃基地计划将如图所示的一块长40 m,宽20 m的矩形空地划分成五块小矩形区域.其中一块正方形空地为育苗区,另一块空地为活动区,其余空地为种植区,分别种植A,B,C三种花卉.活动区一边与育苗区等宽,另一边长是10 m.A,B,C三种花卉每平方米的产值分别是2百元、3百元、4百元.
(1)、在图1中,先将线段CB绕点C顺时针旋转90°,画出旋转后的对应线段CE;再在线段CE上画点F , 连接BF , 使∠CFB=∠A;(2)、在图2中,M , N分别是网格线上和网格内的一点.先过点M画与BC平行的直线l;再在直线l上画一点P , 使NP⊥AB .22. 春回大地,万物复苏,又是一年花季到.某花圃基地计划将如图所示的一块长40 m,宽20 m的矩形空地划分成五块小矩形区域.其中一块正方形空地为育苗区,另一块空地为活动区,其余空地为种植区,分别种植A,B,C三种花卉.活动区一边与育苗区等宽,另一边长是10 m.A,B,C三种花卉每平方米的产值分别是2百元、3百元、4百元. (1)、设育苗区的边长为x m,用含x的代数式表示下列各量:花卉A的种植面积是 , 花卉B的种植面积是 , 花卉C的种植面积是.(2)、育苗区的边长为多少时,A,B两种花卉的总产值相等?(3)、若花卉A与B的种植面积之和不超过 ,求A,B,C三种花卉的总产值之和的最大值.23. 在Rt△ABC中,∠ABC=90°,AB=nBC , P为AB上的一点(不与端点重合),过点P作PM⊥AB交AG于点M , 得到△APM .
(1)、设育苗区的边长为x m,用含x的代数式表示下列各量:花卉A的种植面积是 , 花卉B的种植面积是 , 花卉C的种植面积是.(2)、育苗区的边长为多少时,A,B两种花卉的总产值相等?(3)、若花卉A与B的种植面积之和不超过 ,求A,B,C三种花卉的总产值之和的最大值.23. 在Rt△ABC中,∠ABC=90°,AB=nBC , P为AB上的一点(不与端点重合),过点P作PM⊥AB交AG于点M , 得到△APM . (1)、【问题发现】如图1,当n=1时,P为AB的中点时,CM与BP的数量关系为 ;(2)、【类比探究】如图2,当n=2时,△APM绕点A顺时针旋转,连接CM , BP , 则在旋转过程中CM与BP之间的数量关系是否发生变化?请说明理由;(3)、【拓展延伸】在(2)的条件下,已知AB=4,AP=2,当△APM绕点A顺时针旋转至B , P , M三点共线时,请直接写出线段BM的长.24. 已知,在以O为原点的直角坐标系中,抛物线的顶点为A(﹣1,﹣4),且经过点B(﹣2,﹣3),与x轴分别交于C、D两点.
(1)、【问题发现】如图1,当n=1时,P为AB的中点时,CM与BP的数量关系为 ;(2)、【类比探究】如图2,当n=2时,△APM绕点A顺时针旋转,连接CM , BP , 则在旋转过程中CM与BP之间的数量关系是否发生变化?请说明理由;(3)、【拓展延伸】在(2)的条件下,已知AB=4,AP=2,当△APM绕点A顺时针旋转至B , P , M三点共线时,请直接写出线段BM的长.24. 已知,在以O为原点的直角坐标系中,抛物线的顶点为A(﹣1,﹣4),且经过点B(﹣2,﹣3),与x轴分别交于C、D两点.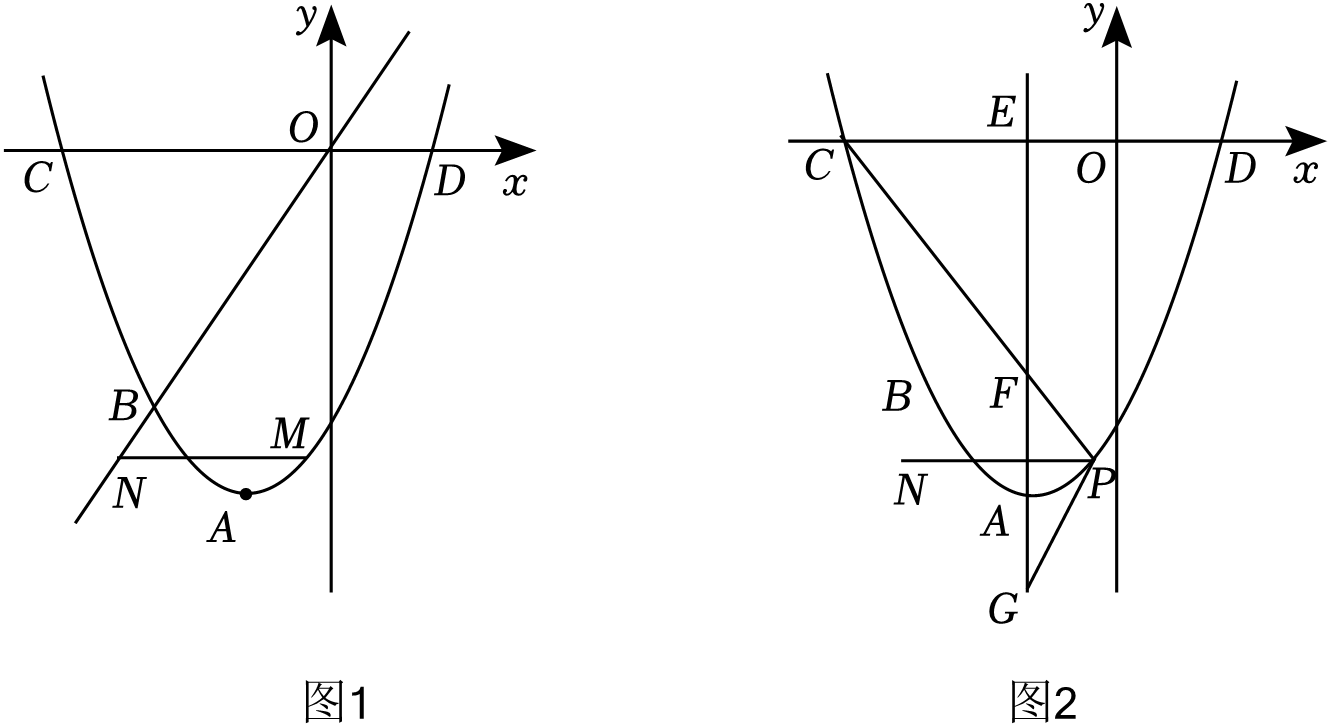 (1)、求该抛物线的函数表达式;(2)、如图(1),点M是抛物线上的一个动点,且在直线OB的下方,过点M作x轴的平行线与直线OB交于点N , 求MN的最大值;(3)、如图(2),过点A的直线交x轴于点E , 且AE∥y轴,点P是抛物线上A、D之间的一个动点,直线PC、PD与AE分别交于F、G两点.当点P运动时,EF+EG是否为定值?若是,试求出该定值;若不是,请说明理由.
(1)、求该抛物线的函数表达式;(2)、如图(1),点M是抛物线上的一个动点,且在直线OB的下方,过点M作x轴的平行线与直线OB交于点N , 求MN的最大值;(3)、如图(2),过点A的直线交x轴于点E , 且AE∥y轴,点P是抛物线上A、D之间的一个动点,直线PC、PD与AE分别交于F、G两点.当点P运动时,EF+EG是否为定值?若是,试求出该定值;若不是,请说明理由.