湖北省黄石市阳新县北部联盟2024年数学第一次中考模拟诊断试卷
试卷更新日期:2024-04-17 类型:中考模拟
一、选择题:本大题共10个小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的,请将其标号在答题卡上涂黑作答.
-
1. 下列各数中,绝对值最大的数是( )
A、-3 B、-2 C、0 D、22. 在一些美术字中,有的汉字是轴对称图形.下面个汉字中,可以看作是轴对称图形的是( )A、 B、
B、 C、
C、 D、
D、 3. 1月9日,中国国家铁路集团有限公司发布数据称,2023年全年,国家铁路完成旅客发送量36.8亿人次,高峰日发送旅客突破2000万人次,全年和高峰日旅客发送量均创历史新高,其中数据“36.8亿”用科学记数法表示为( )A、 B、 C、 D、4. 如图,是由7个大小相同的小正方体堆砌而成的几何体,若从标有①、②、③、④的四个小正方体中取走一个后,余下的几何体与原几何体的主视图相同,则取走的正方体是( )
3. 1月9日,中国国家铁路集团有限公司发布数据称,2023年全年,国家铁路完成旅客发送量36.8亿人次,高峰日发送旅客突破2000万人次,全年和高峰日旅客发送量均创历史新高,其中数据“36.8亿”用科学记数法表示为( )A、 B、 C、 D、4. 如图,是由7个大小相同的小正方体堆砌而成的几何体,若从标有①、②、③、④的四个小正方体中取走一个后,余下的几何体与原几何体的主视图相同,则取走的正方体是( )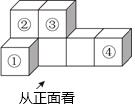 A、① B、② C、③ D、④5. 下列计算正确的是( )A、 B、 C、 D、6. 下列说法正确的是( )A、成语“刻舟求剑”描述的是必然事件 B、了解央视春晚的收视率适合用抽样调查 C、调查某品牌烟花的合格率适合用全面调查 D、如果某彩票的中奖率是1%,那么一次购买100张彩票一定会中奖7. 分式方程 的解是( )A、x=1 B、x=﹣1+ C、x=2 D、无解8. 班长邀请A , B , C , D四位同学参加圆桌会议.如图,班长坐在⑤号座位,则A , B两位同学座位相邻的概率是( )
A、① B、② C、③ D、④5. 下列计算正确的是( )A、 B、 C、 D、6. 下列说法正确的是( )A、成语“刻舟求剑”描述的是必然事件 B、了解央视春晚的收视率适合用抽样调查 C、调查某品牌烟花的合格率适合用全面调查 D、如果某彩票的中奖率是1%,那么一次购买100张彩票一定会中奖7. 分式方程 的解是( )A、x=1 B、x=﹣1+ C、x=2 D、无解8. 班长邀请A , B , C , D四位同学参加圆桌会议.如图,班长坐在⑤号座位,则A , B两位同学座位相邻的概率是( ) A、 B、 C、 D、9. 如图,AB是⊙O的弦,半径OC⊥AB , D为圆周上一点,若∠ADC的度数为35°,则∠ABO的度数为( )
A、 B、 C、 D、9. 如图,AB是⊙O的弦,半径OC⊥AB , D为圆周上一点,若∠ADC的度数为35°,则∠ABO的度数为( ) A、15° B、20° C、25° D、30°10. 已知等腰三角形的周长是10,底边长y是腰长x的函数,则下列图象中,能正确反映y与x的函数关系的是( )A、
A、15° B、20° C、25° D、30°10. 已知等腰三角形的周长是10,底边长y是腰长x的函数,则下列图象中,能正确反映y与x的函数关系的是( )A、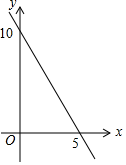 B、
B、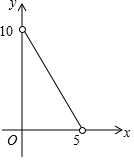 C、
C、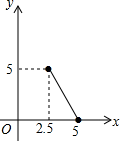 D、
D、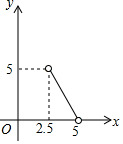
二、填空题(本大题共6个小题,每小题3分,共18分)把答案填在答题卡的相应位置上.
-
11. 写出一个比4小的正无理数 .12. 截止2021年4月中国高速路总里程达16万公里.请将“16万”用科学记数法表示记为.13. 如图,电路上有①、②、③3个开关和一个小灯泡,若任意闭合电路上2个开关,则小灯泡发光的概率为 .
 14. 用长为12米铝合金条制成如图所示的窗框,若窗框的高为x米,当x等于时窗户的透光面积最大(铝合金条的宽度不计).
14. 用长为12米铝合金条制成如图所示的窗框,若窗框的高为x米,当x等于时窗户的透光面积最大(铝合金条的宽度不计). 15. 如图,平行四边形ABCD中,AB=4, , ∠ABC=120°,点E在AD上,将△ABE沿BE折叠得到 , 若点恰好在线段CE上,则AE的长为 .
15. 如图,平行四边形ABCD中,AB=4, , ∠ABC=120°,点E在AD上,将△ABE沿BE折叠得到 , 若点恰好在线段CE上,则AE的长为 . 16. 抛物线 (a , b , c是常数)经过 , , , 三点,给出下列四个结论:①;②若时,y随x增加而减少,则;③若在抛物线上,则;④;其中正确的结论是 . (填写序号).
16. 抛物线 (a , b , c是常数)经过 , , , 三点,给出下列四个结论:①;②若时,y随x增加而减少,则;③若在抛物线上,则;④;其中正确的结论是 . (填写序号).三、解答题(本大题共9个小题,共72分.解答应写出文字说明、证明过程或演算步骤,并且写在答题卡上每题对应的答题区域内.)
-
17. 先化简,再求值 ,其中 , .18. 如图,点D , E , F分别是的边 , , 上的点, , ,
 (1)、求证:四边形为平行四边形;(2)、若 , 直接写出的值为 .19. “感受数学魅力,提升数学素养”,思远中学在校开展了数学文化知识竞赛,现从七年级和八年级参加竞赛的学生中各随机抽取了10名学生的成绩进行整理、描述和分析(单位:分,满分100分,成绩均不低于70分,90分及90分以上为优秀),并将学生竞赛成绩分为A , B , C三个等级:A:70≤x<80,B:80≤x<90,C:90≤x<100.
(1)、求证:四边形为平行四边形;(2)、若 , 直接写出的值为 .19. “感受数学魅力,提升数学素养”,思远中学在校开展了数学文化知识竞赛,现从七年级和八年级参加竞赛的学生中各随机抽取了10名学生的成绩进行整理、描述和分析(单位:分,满分100分,成绩均不低于70分,90分及90分以上为优秀),并将学生竞赛成绩分为A , B , C三个等级:A:70≤x<80,B:80≤x<90,C:90≤x<100.下面给出了部分信息:
抽取的七年级10名学生的竞赛成绩为:75,76,84,84,84,86,86,94,95,96;
抽取的八年级10名学生的竞赛成绩在B等级的为:81,83,84,88,88.
两个年级抽取的学生成绩的平均数、中位数、众数如下表所示:
学生
平均数
中位数
众数
七年级
86
85
b
八年级
86
a
88
抽取的八年级学生竞赛成绩扇形统计图:

根据以上信息,解答下列问题:
(1)、填空:a= , b= , ;(2)、根据以上数据,请你对七年级竞赛成绩作出分析?(写一条即可);(3)、若八年级共有300名学生参赛,请你估计八年级参赛学生中成绩为优秀的人数.20. 如图,海面上一艘船由西向东航行,在A处测得正东方向上一座灯塔的最高点C的仰角为31°,再向东继续航行60m到达B处,测得该灯塔的最高点C的仰角为45°.根据测得的数据,计算这座灯塔的高度CD(结果取整数).参考数据:sin31°≈0.52,cos31°≈0.86,tan31°≈0.60 21. 如图是由小正方形组成的网格,每个小正方形的顶点叫做格点,中,A是格线上的点,仅用无刻度的直尺在给定网格中完成画图.
21. 如图是由小正方形组成的网格,每个小正方形的顶点叫做格点,中,A是格线上的点,仅用无刻度的直尺在给定网格中完成画图. (1)、在图(1)中,取的中点M;将沿着方向平移至;(2)、在图(2)中,将线段绕C逆时针旋转至(点E为点B的对应点);过点E作于F .22. 网络直播带货已成为一种新业态,某网店尝试用60天的时间,按单价随天数而变化的直播带货模式销售一种成本为10元/每件的商品,经过统计得到此商品的日销售量(件)、销售单价(元/件)在第天(x为正整数)销售的相关信息:
(1)、在图(1)中,取的中点M;将沿着方向平移至;(2)、在图(2)中,将线段绕C逆时针旋转至(点E为点B的对应点);过点E作于F .22. 网络直播带货已成为一种新业态,某网店尝试用60天的时间,按单价随天数而变化的直播带货模式销售一种成本为10元/每件的商品,经过统计得到此商品的日销售量(件)、销售单价(元/件)在第天(x为正整数)销售的相关信息:①与满足一次函数关系,且第1天的日销售量为98件,第4天的日销售量为92件;
②与函数关系如下图所示;
 (1)、第5天的日销售量件;与的函数关系式为 .(2)、在这60天中,网店哪天销售该商品的日利润最大?最大是多少元?(3)、在这60天中,共有多少天日利润不低于2418元?23. 倡导垃圾分类,共享绿色生活.为了对回收的垃圾进行更精准的分类,某机器人公司研发出A型和B型两款垃圾分拣机器人,已知2台A型机器人和5台B型机器人同时工作2小时共分拣垃圾3.6吨,3台A型机器人和2台B型机器人同时工作5小时共分拣垃圾8吨.(1)、1台A型机器人和1台B型机器人每小时各分拣垃圾多少吨?(2)、某垃圾处理厂计划向机器人公司购进一批A型和B型垃圾分拣机器人,机器人公司的报价如下表:
(1)、第5天的日销售量件;与的函数关系式为 .(2)、在这60天中,网店哪天销售该商品的日利润最大?最大是多少元?(3)、在这60天中,共有多少天日利润不低于2418元?23. 倡导垃圾分类,共享绿色生活.为了对回收的垃圾进行更精准的分类,某机器人公司研发出A型和B型两款垃圾分拣机器人,已知2台A型机器人和5台B型机器人同时工作2小时共分拣垃圾3.6吨,3台A型机器人和2台B型机器人同时工作5小时共分拣垃圾8吨.(1)、1台A型机器人和1台B型机器人每小时各分拣垃圾多少吨?(2)、某垃圾处理厂计划向机器人公司购进一批A型和B型垃圾分拣机器人,机器人公司的报价如下表:型号
原价
购买量少于30台
购买量不少于30台
A型
20万元/台
原价购买
打九折
B型
12万元/台
原价购买
打八折
①若要求这批机器人每小时一共能分拣垃圾20吨.设其中购买A型机器人x台(10≤x≤35),购买两种机器人总费用为W万元.求W与x的函数关系式,并说明如何购买总费用最少;
②为了加快垃圾分拣速度,垃圾处理厂计划用不超过140万元增购这两种机器人共10台,机器人公司全部以打折后价格销售,这10台机器人每小时最多处理多少吨垃圾?
24. 如图1,已知抛物线与轴交于点 , , 与轴交于点 , 连接 . (1)、求 , 的值及直线的解析式;(2)、如图1,点是抛物线上位于直线上方的一点,连接交于点 , 过作轴于点 , 交于点 ,
(1)、求 , 的值及直线的解析式;(2)、如图1,点是抛物线上位于直线上方的一点,连接交于点 , 过作轴于点 , 交于点 ,(ⅰ)若 , 求点P的坐标,
(ⅱ)连接 , , 记的面积为 , 的面积为 , 求的最大值;
(3)、如图2,将抛物线位于轴下方面的部分不变,位于轴上方面的部分关于轴对称,得到新的图形,将直线向下平移个单位,得到直线 , 若直线与新的图形有四个不同交点,请直接写出的取值范围.