湖北省荆州市2024年中考数学模拟试卷
试卷更新日期:2024-04-17 类型:中考模拟
一、选择题(每小题3分,共30分)
-
1. 下列各数中,为有理数的是( )A、 B、 C、π D、2. 下面哪个图象不是正方体的表面展开图( )A、
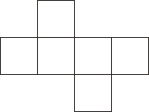 B、
B、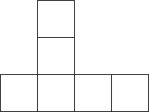 C、
C、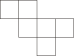 D、
D、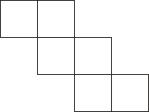 3. 下列说法正确的是( )A、射击运动员射击一次,命中十环是必然事件. B、两个负数相乘,积是正数是不可能事件. C、了解某品牌手机电池待机时间用全面调查 D、了解荆州市中学生目前的睡眠情况用抽样调查.4. 下列运算正确的是( )A、2 B、a8÷a2=a4 C、(a﹣1)2=a2﹣1 D、(a5)2=a105. 若m>n , 下列不等式不一定成立的是( )A、m2>n2 B、﹣3m<﹣3n C、 D、m+3>n+36. 如图, , , 若 , 则的度数是( )
3. 下列说法正确的是( )A、射击运动员射击一次,命中十环是必然事件. B、两个负数相乘,积是正数是不可能事件. C、了解某品牌手机电池待机时间用全面调查 D、了解荆州市中学生目前的睡眠情况用抽样调查.4. 下列运算正确的是( )A、2 B、a8÷a2=a4 C、(a﹣1)2=a2﹣1 D、(a5)2=a105. 若m>n , 下列不等式不一定成立的是( )A、m2>n2 B、﹣3m<﹣3n C、 D、m+3>n+36. 如图, , , 若 , 则的度数是( )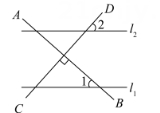 A、35° B、45° C、55° D、65°7. 如图,在四边形ABCD中,下列条件不能判定四边形ABCD是平行四边形的是( )
A、35° B、45° C、55° D、65°7. 如图,在四边形ABCD中,下列条件不能判定四边形ABCD是平行四边形的是( ) A、OA=OC , OB=OD B、AB=DC , AD=BC C、AD∥BC , AB=DC D、AB∥DC , AB=DC8. 已知一次函数y=kx+b(k≠0)的图象如图所示,则y=﹣bx﹣k的图象一定不经过( )
A、OA=OC , OB=OD B、AB=DC , AD=BC C、AD∥BC , AB=DC D、AB∥DC , AB=DC8. 已知一次函数y=kx+b(k≠0)的图象如图所示,则y=﹣bx﹣k的图象一定不经过( ) A、第一象限 B、第二象限 C、第三象限 D、第四象限9. 若菱形的周长为16,高为2,则菱形两邻角的度数之比为( )A、4:1 B、5:1 C、6:1 D、7:110. 已知二次函数y=ax2+bx+c(a , b , c为常数,a≠0)的图象如图所示,有如下结论:①abc>0;②2a+b=1;③3a+c>0;④方程ax2+bx+c有两个不相等的实数根;其中正确的个数为( )个.
A、第一象限 B、第二象限 C、第三象限 D、第四象限9. 若菱形的周长为16,高为2,则菱形两邻角的度数之比为( )A、4:1 B、5:1 C、6:1 D、7:110. 已知二次函数y=ax2+bx+c(a , b , c为常数,a≠0)的图象如图所示,有如下结论:①abc>0;②2a+b=1;③3a+c>0;④方程ax2+bx+c有两个不相等的实数根;其中正确的个数为( )个. A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题(每小题3分,共15分)
-
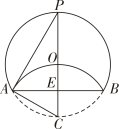
11. 据统计,2024年春节假日期间,荆州市累计接待游客4095000人次,4095000用科学记数法可表示为 .12. 若代数式有意义,则实数x的取值范围为13. 分解因式:3ax2﹣12axy+12ay2= .14. 已知 , , 都在反比例函数图象上,且满足 , 则 , , 的大小关系是 . (用“<”连接)15. 如图,将圆形纸片折叠使弧AB经过圆心O , 过点O作半径于点E , 点P为圆上一点,则的度数为 .
三、解答题(共75分)
-
16. 计算: .17. 已知m , n是方程x2+3x﹣4=0的两根,求2m2+5m﹣n﹣3的值.18. A,B两种机器人都被用来搬运化工原料,A型机器人比B型机器人每小时多搬运30kg,A型机器人搬运900kg所用时间与B型机器人搬运600kg所用时间相等,求A型机器人每小时搬运多少化工原料.19. “除夕”是我国最重要的传统佳节,成都市民历来有“除夕”夜吃“饺子”的习俗,我市某食品厂为了解市民对去年销售较好的猪肉馅饺、素菜馅饺、羊肉馅饺、牛肉馅饺(以下分别用A、B、C、D表示)这四种不同口味饺子的喜爱情况,在节前对某居民区进行了抽样调查,并将调查情况绘制成如图两幅统计图(尚不完整).
请根据以上信息回答:
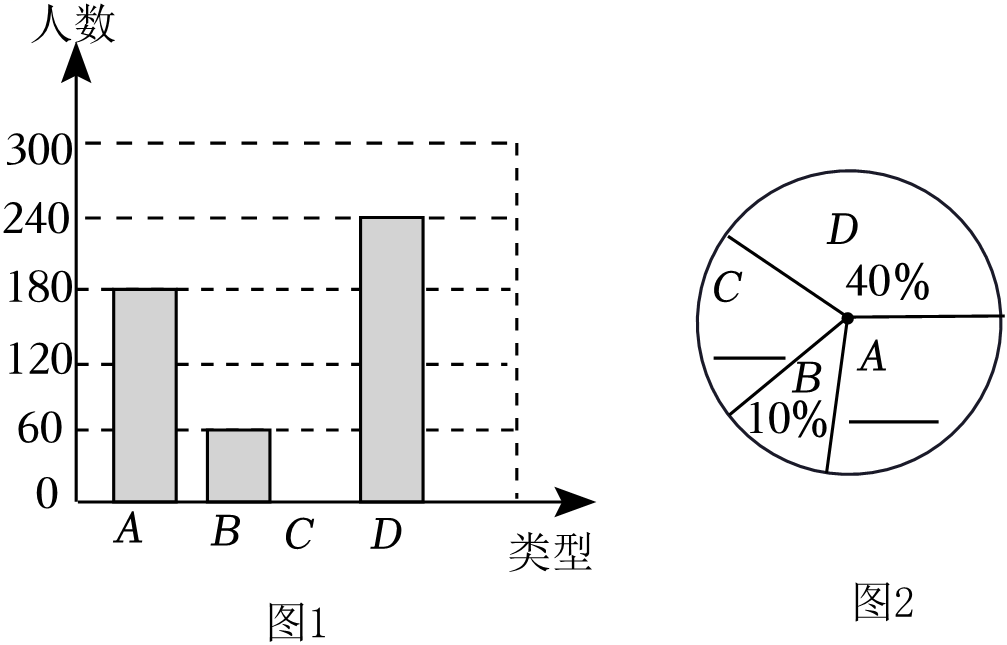 (1)、本次参加抽样调查的居民有 人?(2)、将两幅不完整的图补充完整;(3)、若有外型完全相同的A、B、C、D饺各一个,煮熟后,小王吃了两个,用列表或画树状图的方法,求他两个都吃到肉馅饺(A、C、D)的概率.20. 如图,在的正方形网格中,每个小正方形的顶点称为格点,的顶点均在格点上.按要求完成下列画图.(要求:用无刻度直尺,保留必要的画图痕迹,不写画法)
(1)、本次参加抽样调查的居民有 人?(2)、将两幅不完整的图补充完整;(3)、若有外型完全相同的A、B、C、D饺各一个,煮熟后,小王吃了两个,用列表或画树状图的方法,求他两个都吃到肉馅饺(A、C、D)的概率.20. 如图,在的正方形网格中,每个小正方形的顶点称为格点,的顶点均在格点上.按要求完成下列画图.(要求:用无刻度直尺,保留必要的画图痕迹,不写画法)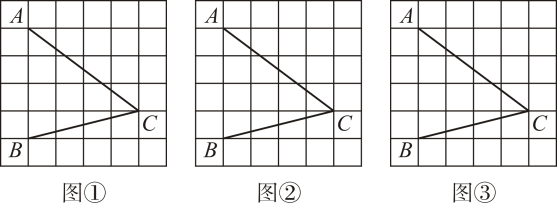 (1)、在图①中画出一个 , 使 , D为格点(点D不在点C处):(2)、在图②中的边BC上找一点E , 连接AE , 使;(3)、在图③中的边BC上找一点F , 使点F到AB和AC所在直线的距离相等.21. 如图,已知D为上一点,点C在直径BA的延长线上,BE与相切,交CD的延长线于点E , 且 .
(1)、在图①中画出一个 , 使 , D为格点(点D不在点C处):(2)、在图②中的边BC上找一点E , 连接AE , 使;(3)、在图③中的边BC上找一点F , 使点F到AB和AC所在直线的距离相等.21. 如图,已知D为上一点,点C在直径BA的延长线上,BE与相切,交CD的延长线于点E , 且 .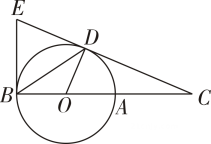 (1)、证明:CE是的切线;(2)、若 , , ①求的半径;②求BD的长.22. 某公司电商平台,在元旦期间举行了商品打折促销活动,经市场调查发现,某种商品的周销售量y(件)是关于售价x(元/件)的一次函数,下表列出了该商品的售价x , 周销售量y , 周销售利润W(元)的三组对应数据.
(1)、证明:CE是的切线;(2)、若 , , ①求的半径;②求BD的长.22. 某公司电商平台,在元旦期间举行了商品打折促销活动,经市场调查发现,某种商品的周销售量y(件)是关于售价x(元/件)的一次函数,下表列出了该商品的售价x , 周销售量y , 周销售利润W(元)的三组对应数据.x
40
70
90
y
240
120
40
W
4800
6000
2800
(1)、求y关于x的函数解析式(不要求写出自变量的取值范围);(2)、若该商品进价a(元/件),售价x为多少时,周销售利润W最大?并求出此时的最大利润;(3)、后来,该商品进价提高了m(元/件)(m>0),公司为回馈消费者,规定该商品售价x不得超过55(元/件),且该商品在今后的销售中,周销售量与售价仍满足(1)中的函数关系,若周销售最大利润是5400元,求m的值.23.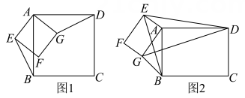 (1)、如图1,已知正方形AEFG与正方形ABCD , 将正方形AEFG绕点A按逆时针方向旋转,求证: , 且;(2)、如图2,将(1)中的两个正方形分别改成矩形AEFG和矩形ABCD , 且 , , , 将矩形AEFG绕点A顺时针方向旋转,连接DE , BG , 在旋转过程中,的值是定值,请求出这个定值.24. 如图,直线y=x﹣3与x轴、y轴分别交于点B、点C , 经过B , C两点的抛物线y=﹣x2+mx+n与x轴的另一个交点为A , 顶点为P .
(1)、如图1,已知正方形AEFG与正方形ABCD , 将正方形AEFG绕点A按逆时针方向旋转,求证: , 且;(2)、如图2,将(1)中的两个正方形分别改成矩形AEFG和矩形ABCD , 且 , , , 将矩形AEFG绕点A顺时针方向旋转,连接DE , BG , 在旋转过程中,的值是定值,请求出这个定值.24. 如图,直线y=x﹣3与x轴、y轴分别交于点B、点C , 经过B , C两点的抛物线y=﹣x2+mx+n与x轴的另一个交点为A , 顶点为P . (1)、求抛物线的解析式;(2)、在该抛物线的对称轴上是否存在点Q , 使以C , P , Q为顶点的三角形为直角三角形?若存在,求出所有符合条件的点Q的坐标;若不存在,请说明理由.(3)、将该抛物线在x轴上方的部分沿x轴向下翻折,图象的其余部分保持不变,翻折后的图象与原图象x轴下方的部分组成一个“M”形状的图象,若直线y=x+b与该“M”形状的图象部分恰好有三个公共点,求b的值.
(1)、求抛物线的解析式;(2)、在该抛物线的对称轴上是否存在点Q , 使以C , P , Q为顶点的三角形为直角三角形?若存在,求出所有符合条件的点Q的坐标;若不存在,请说明理由.(3)、将该抛物线在x轴上方的部分沿x轴向下翻折,图象的其余部分保持不变,翻折后的图象与原图象x轴下方的部分组成一个“M”形状的图象,若直线y=x+b与该“M”形状的图象部分恰好有三个公共点,求b的值.