湖北省随州市2024年联考中考一模数学试题
试卷更新日期:2024-04-17 类型:中考模拟
一、选择题(共10题每小题3分,共30分,在每题给出的四个选项中,只有一项符合题目要求
-
1. 2024的相反数是( )A、2024 B、 C、 D、不存在2. 2023年长沙国际马拉松在芙蓉中路(贺龙体育中心东广场旁)起跑,来自国内外的26000名跑友汇成一片红色的海洋驰聘在长马赛道上,他们用脚步丈量星城,感受一江两岸、山水洲城的魅力,图①是此次全程马拉松男子组颁奖现场.图②是领奖台的示意图,则此领奖台从正面看到的平面图形是( )
 A、
A、 B、
B、 C、
C、 D、
D、 3. 不等式组的解集在数轴上表示正确的是( )A、
3. 不等式组的解集在数轴上表示正确的是( )A、 B、
B、 C、
C、 D、
D、 4. 下列说法正确的是( )A、了解我是“创文明、树新风”活动的市民知晓情况,适合采用全面调查 B、在同圆中,等弧所对的圆心角相等 C、学校将选择初三的一名学生参加市里的数学竞赛活动,甲、乙、丙三位同学初三一学期的数学成绩的方差分别为 , , , 选择乙同学去最合适 D、可能性是的事件在一次实验中一定会发生5. 下列各运算中,正确的运算是( )A、 B、(2a)3=8a3 C、a8÷a4=a2 D、(a﹣b)2=a2﹣b26. 已知直线 , 将含有的直角三角尺按如图方式放置(),其中A,C两点分别落在直线m,n上,若 , 则的度数为( )
4. 下列说法正确的是( )A、了解我是“创文明、树新风”活动的市民知晓情况,适合采用全面调查 B、在同圆中,等弧所对的圆心角相等 C、学校将选择初三的一名学生参加市里的数学竞赛活动,甲、乙、丙三位同学初三一学期的数学成绩的方差分别为 , , , 选择乙同学去最合适 D、可能性是的事件在一次实验中一定会发生5. 下列各运算中,正确的运算是( )A、 B、(2a)3=8a3 C、a8÷a4=a2 D、(a﹣b)2=a2﹣b26. 已知直线 , 将含有的直角三角尺按如图方式放置(),其中A,C两点分别落在直线m,n上,若 , 则的度数为( )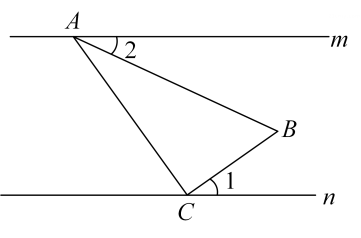 A、 B、 C、 D、7. 如图,将正方形和正五边形的中心重合,按如图位置放置,连接、 , 则( )
A、 B、 C、 D、7. 如图,将正方形和正五边形的中心重合,按如图位置放置,连接、 , 则( ) A、 B、 C、 D、8. 如图,分别切于两点,点在优弧上, , 则的度数为( )
A、 B、 C、 D、8. 如图,分别切于两点,点在优弧上, , 则的度数为( ) A、 B、 C、 D、9. 日照灯塔是日照海滨港口城市的标志性建筑之一,主要为日照近海及进出日照港的船舶提供导航服务.数学小组的同学要测量灯塔的高度,如图所示,在点B处测得灯塔最高点A的仰角 , 再沿方向前进至C处测得最高点A的仰角 , , 则灯塔的高度大约是( )(结果精确到 , 参考数据: , )
A、 B、 C、 D、9. 日照灯塔是日照海滨港口城市的标志性建筑之一,主要为日照近海及进出日照港的船舶提供导航服务.数学小组的同学要测量灯塔的高度,如图所示,在点B处测得灯塔最高点A的仰角 , 再沿方向前进至C处测得最高点A的仰角 , , 则灯塔的高度大约是( )(结果精确到 , 参考数据: , ) A、 B、 C、 D、10. 如图,抛物线的对称轴为直线 , 且过点 . 现有以下结论:①;②;③对于任意实数 , 都有;④若点是图象上任意两点,且 , 则 , 其中正确的结论是( )
A、 B、 C、 D、10. 如图,抛物线的对称轴为直线 , 且过点 . 现有以下结论:①;②;③对于任意实数 , 都有;④若点是图象上任意两点,且 , 则 , 其中正确的结论是( ) A、①② B、②③④ C、①②④ D、①②③④
A、①② B、②③④ C、①②④ D、①②③④二、填空题(共5题,每小题3分,共15分
-
11. 计算: .12. 请写出一组k、b的值,使一次函数的图象经过第一、三、四象限: .13. 小明从《红星照耀中国》,《红岩》,《长征》,《钢铁是怎样炼成的》四本书中随机挑选一本,其中拿到《红星照耀中国》这本书的概率为 .14. 我国古代著作《四元玉鉴》记载“买椽多少”问题:“六贯二百一十钱,倩人去买几株椽.每株脚钱三文足,无钱准与一株椽.”其大意:现请人代买一批椽,这批椽的价钱为6210文.如果每株椽的运费是3文,那么少拿一株椽后,剩下的椽的运费恰好等于一株椽的价钱,试问6210文能买多少株椽?若设这批椽的数量为x株,则可列分式方程为 .15. 如图,在等边△ABC中, , 点P是边BC上的动点,将△ABP绕点A逆时针旋转得到△ACQ , 点D是AC边的中点,连接DQ , 则DQ的最小值是 .

三、解答题(共9题,共75分,解答就应写出文字说明、证明过程或演算步骤
-
16. 计算: .17. 如图,点 分别在菱形 的边 上, .求证:
 18. 2023年5月10日,搭载天舟六号货运飞船的长征七号遥七运载火箭,在我国文昌航天发射场点火发射成功.为了普及航空航天科普知识,某校组织学生去文昌卫星发射中心参观学习.已知该校租用甲、乙两种不同型号的客车共15辆,租用1辆甲型客车需600元,1辆乙型客车需500元,租车费共8000元.问甲、乙两种型号客车各租多少辆?19. 某校在八年级开展了以“争创文明城市,建设文明校园”为主题的系列艺术展示活动,活动项目有“绘画展示”“书法展示”“文艺表演”“即兴演讲”四组(依次记为A , B , C , D).学校要求八年级全体学生必须参加且只能参加其中的一个项目,为了解八年级学生对这几项活动的喜爱程度,随机抽取了部分八年级学生进行调查,并将调查的结果绘制成两幅不完整的统计图.
18. 2023年5月10日,搭载天舟六号货运飞船的长征七号遥七运载火箭,在我国文昌航天发射场点火发射成功.为了普及航空航天科普知识,某校组织学生去文昌卫星发射中心参观学习.已知该校租用甲、乙两种不同型号的客车共15辆,租用1辆甲型客车需600元,1辆乙型客车需500元,租车费共8000元.问甲、乙两种型号客车各租多少辆?19. 某校在八年级开展了以“争创文明城市,建设文明校园”为主题的系列艺术展示活动,活动项目有“绘画展示”“书法展示”“文艺表演”“即兴演讲”四组(依次记为A , B , C , D).学校要求八年级全体学生必须参加且只能参加其中的一个项目,为了解八年级学生对这几项活动的喜爱程度,随机抽取了部分八年级学生进行调查,并将调查的结果绘制成两幅不完整的统计图.
根据以上信息,解答下列问题:
(1)、本次一共抽样调查了名学生;(2)、将条形统计图补充完整;(3)、若该校八年级共有600名学生,请估计该校八年级学生选择“文艺表演”的人数;(4)、学校从这四个项目中随机抽取两项参加“全市中学生才艺展示活动”.用列表法或画树状图法求出恰好抽到“绘画展示”和“书法展示”的概率.20. 已知一次函数y=kx+b与反比例函数y的图象交于A(﹣3,2)、B(1,n)两点. (1)、求一次函数和反比例函数的表达式;(2)、求△AOB的面积;(3)、结合图像直接写出不等式kx+b的解集.21. 如图,四边形是的内接四边形,是直径,是的中点,过点作交的延长线于点 .
(1)、求一次函数和反比例函数的表达式;(2)、求△AOB的面积;(3)、结合图像直接写出不等式kx+b的解集.21. 如图,四边形是的内接四边形,是直径,是的中点,过点作交的延长线于点 .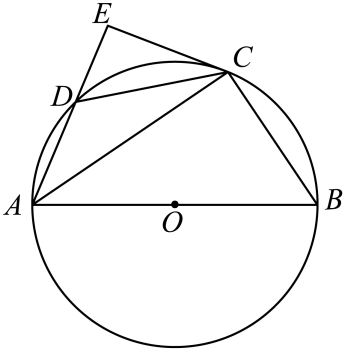 (1)、求证:是的切线;(2)、若 , , 求的长.22. “端午节”吃粽子是中国传统习俗,在“端午节”来临前,某超市购进一种品牌粽子,每盒进价是40元,并规定每盒售价不得少于50元,日销售量不低于350盒,根据以往销售经验发现,当每盒售价定为50元时,日销售量为500盒,每盒售价每提高1元,日销售量减少10盒,设每盒售价为x元,日销售量为p盒.(1)、当时,;(2)、当每盒售价定为多少元时,日销售利润W(元)最大?最大利润是多少?(3)、小强说:“当日销售利润最大时,日销售额不是最大,”小红说:“当日销售利润不低于8000元时,每盒售价x的范围为 . ”你认为他们的说法正确吗?若正确,请说明理由;若不正确,请直接写出正确的结论.23.
(1)、求证:是的切线;(2)、若 , , 求的长.22. “端午节”吃粽子是中国传统习俗,在“端午节”来临前,某超市购进一种品牌粽子,每盒进价是40元,并规定每盒售价不得少于50元,日销售量不低于350盒,根据以往销售经验发现,当每盒售价定为50元时,日销售量为500盒,每盒售价每提高1元,日销售量减少10盒,设每盒售价为x元,日销售量为p盒.(1)、当时,;(2)、当每盒售价定为多少元时,日销售利润W(元)最大?最大利润是多少?(3)、小强说:“当日销售利润最大时,日销售额不是最大,”小红说:“当日销售利润不低于8000元时,每盒售价x的范围为 . ”你认为他们的说法正确吗?若正确,请说明理由;若不正确,请直接写出正确的结论.23. (1)、【问题提出】如图①,在正方形中,点分别在边上, . 请判断与的数量关系,并说明理由.(2)、【类比探究】如图②,在矩形中, , 将矩形沿折叠,使点落在边上的点处,得到四边形交于点 , 连接交于点 . 则与之间的数量关系为 .(3)、【拓展应用】在(2)的条件下,若 , , 则的长为 .24. 如图,抛物线经过 , 两点,于轴交于点 , 为第一象限抛物线上的动点,连接 , , , , 与相交于点 .
(1)、【问题提出】如图①,在正方形中,点分别在边上, . 请判断与的数量关系,并说明理由.(2)、【类比探究】如图②,在矩形中, , 将矩形沿折叠,使点落在边上的点处,得到四边形交于点 , 连接交于点 . 则与之间的数量关系为 .(3)、【拓展应用】在(2)的条件下,若 , , 则的长为 .24. 如图,抛物线经过 , 两点,于轴交于点 , 为第一象限抛物线上的动点,连接 , , , , 与相交于点 . (1)、求抛物线的解析式;(2)、设的面积为 , 的面积为 , 当时,求点的坐标;(3)、是否存在点 , 使 , 若存在,请求出点的坐标;若不存在,说明理由.
(1)、求抛物线的解析式;(2)、设的面积为 , 的面积为 , 当时,求点的坐标;(3)、是否存在点 , 使 , 若存在,请求出点的坐标;若不存在,说明理由.