湖北省孝感市孝南区2024年中考一模数学试题
试卷更新日期:2024-04-17 类型:中考模拟
一、选择题(共10题,每题3分,共30分.在每题给出的四个选项中,只有一项符合题目要求)
-
1. 下列四个数中,最小的数是( )A、 B、0 C、 D、22. 下面四个几何体中,俯视图为四边形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 关于的一元一次不等式的解集在数轴上的表示如图所示,则的值为( )
3. 关于的一元一次不等式的解集在数轴上的表示如图所示,则的值为( ) A、3 B、2 C、1 D、04. 下列计算正确的是( )A、 B、 C、 D、5. 下列说法正确的是( )A、了解“湖北省初中生每天体育运动时间的情况”最适合的调查方式是全面调查 B、“打开电视机,恰好播放新闻”这一事件是不可能事件 C、大量重复试验时,随着试验次数的增加,频率一般会越来越接近概率 D、甲、乙两人跳绳各10次,其成绩的平均数相等, , 则甲的成绩比乙稳定6. 已知是一元二次方程的两个实数根,下列结论错误的是( )A、 B、 C、 D、7. 如图,平行于主光轴的光线和经过凹透镜的折射后,折射光线 , 的反向延长线交于主光轴上一点P . 若 , 则的度数是( )
A、3 B、2 C、1 D、04. 下列计算正确的是( )A、 B、 C、 D、5. 下列说法正确的是( )A、了解“湖北省初中生每天体育运动时间的情况”最适合的调查方式是全面调查 B、“打开电视机,恰好播放新闻”这一事件是不可能事件 C、大量重复试验时,随着试验次数的增加,频率一般会越来越接近概率 D、甲、乙两人跳绳各10次,其成绩的平均数相等, , 则甲的成绩比乙稳定6. 已知是一元二次方程的两个实数根,下列结论错误的是( )A、 B、 C、 D、7. 如图,平行于主光轴的光线和经过凹透镜的折射后,折射光线 , 的反向延长线交于主光轴上一点P . 若 , 则的度数是( ) A、 B、 C、 D、8. 如图,小正方形的边长均为1,则下列图中的三角形(阴影部分)与△ABC相似的是( )
A、 B、 C、 D、8. 如图,小正方形的边长均为1,则下列图中的三角形(阴影部分)与△ABC相似的是( ) A、
A、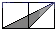 B、
B、 C、
C、 D、
D、 9. 如图,线段在平面直角坐标系内,A点坐标为 , 线段绕原点O旋转 , 得到线段 , 则点的坐标为( )
9. 如图,线段在平面直角坐标系内,A点坐标为 , 线段绕原点O旋转 , 得到线段 , 则点的坐标为( ) A、 B、 C、或 D、或10. 如图是二次函数图象的一部分,其对称轴是 , 且过点 , 如下结论:①;②;③;④若 , 是抛物线上的两点,则;⑤;其中正确的结论有( )
A、 B、 C、或 D、或10. 如图是二次函数图象的一部分,其对称轴是 , 且过点 , 如下结论:①;②;③;④若 , 是抛物线上的两点,则;⑤;其中正确的结论有( ) A、1个 B、2个 C、3 个 D、4个
A、1个 B、2个 C、3 个 D、4个二、填空题(共5题,每题3分,共15分)
-
11. 计算 的结果为 .12. 如图,点B、E、C、F在一条直线上,AB∥DE,且AB=DE,请添加一个条件 , 使△ABC≌△DEF.
 13. 喜迎二十大,“龙舟故里”赛龙舟.丹丹在汨罗江国际龙舟竞渡中心广场点处观看200米直道竞速赛.如图所示,赛道为东西方向,赛道起点位于点的北偏西方向上,终点位于点的北偏东方向上,米,则点到赛道的距离约为米(结果保留整数,参考数据:).
13. 喜迎二十大,“龙舟故里”赛龙舟.丹丹在汨罗江国际龙舟竞渡中心广场点处观看200米直道竞速赛.如图所示,赛道为东西方向,赛道起点位于点的北偏西方向上,终点位于点的北偏东方向上,米,则点到赛道的距离约为米(结果保留整数,参考数据:). 14. 某市体育中考新增了“三大球”选考项目,即A . 足球运球绕杆;B . 排球垫球;C . 篮球运球绕杆.在体育课时,体育老师让每名学生需从这三项中随机选取一项进行训练.小方和小迪参加了这次“三大球”体育课训练,则他们选取同一训练项目的概率为 .15. 中国古代数学家赵爽在为《周髀算经》作注解时,用4个全等的直角三角形拼成正方形(如图),并用它证明了勾股定理,这个图被称为“赵爽弦图”.作 , 若 , 则的值为 .
14. 某市体育中考新增了“三大球”选考项目,即A . 足球运球绕杆;B . 排球垫球;C . 篮球运球绕杆.在体育课时,体育老师让每名学生需从这三项中随机选取一项进行训练.小方和小迪参加了这次“三大球”体育课训练,则他们选取同一训练项目的概率为 .15. 中国古代数学家赵爽在为《周髀算经》作注解时,用4个全等的直角三角形拼成正方形(如图),并用它证明了勾股定理,这个图被称为“赵爽弦图”.作 , 若 , 则的值为 .
三、解答题(共9题,共75分,解答应写出文字说明、证明过程或演算步骤)
-
16. 计算: .17. 求证:对角线互相垂直的平行四边形是菱形.
小红同学根据题意画出了图形,并写出了已知和求证的一部分,请你补全已知和求证,并写出证明过程.
已知:如图,在▱ABCD中,对角线AC , BD交于点O , ▲ .
求证: ▲ .
 18. 为改善居民出行环境,相关部门决定对某路段进行施工改造.施工全长600米,为了早日方便市民,实际施工时,每天的工效比原计划增加 , 结果提前2天完成这一任务,求原计划每天施工多少米?19. 某初中学校为了更好地开展“家国情•诵经典”读书活动,需要先制定学生每天阅读时间(m/分钟)的合格标准.为此从全校学生中随机抽取200人进行问卷调查,获取了他们每人平均每天阅读时间的数据(m/分钟).将收集的数据分为A , B , C , D , E五个等级,绘制成如下统计图表(尚不完整):
18. 为改善居民出行环境,相关部门决定对某路段进行施工改造.施工全长600米,为了早日方便市民,实际施工时,每天的工效比原计划增加 , 结果提前2天完成这一任务,求原计划每天施工多少米?19. 某初中学校为了更好地开展“家国情•诵经典”读书活动,需要先制定学生每天阅读时间(m/分钟)的合格标准.为此从全校学生中随机抽取200人进行问卷调查,获取了他们每人平均每天阅读时间的数据(m/分钟).将收集的数据分为A , B , C , D , E五个等级,绘制成如下统计图表(尚不完整):平均每天阅读时间统计表
等级
组中值
人数(频数)
A()
15
x
B()
25
65
C()
35
10
D()
45
80
E()
55
y

请根据图表中的信息,解答下列问题:
(1)、则x的值为 , C等级所对应的扇形圆心角的度数为°;(2)、这组数据的中位数所在的等级是;(3)、若抽取的200人的每天平均阅读时间约为32分钟,请你从平均数、中位数中选取一个量,为该校制定一个学生每天阅读时间的合格标准(时间取整数分钟),并用统计量说明其合理性.20. 如图,正比例函数的图像与反比例函数的图像都经过点 . (1)、求点A的坐标和反比例函数表达式.(2)、若点在该反比例函数图象上,且它到y轴距离小于3,请根据图像直接写出n的取值范围.21. 在中, , 平分交于点E , D是边上一点,以为直径的经过点E , 且交于点F .
(1)、求点A的坐标和反比例函数表达式.(2)、若点在该反比例函数图象上,且它到y轴距离小于3,请根据图像直接写出n的取值范围.21. 在中, , 平分交于点E , D是边上一点,以为直径的经过点E , 且交于点F . (1)、求证:是的切线;(2)、若 , , 求图中阴影部分的面积.22. 园林基地计划投资种植花卉及树木,已知种植树木的利润与投资量x成正比例关系,种植花卉的利润与投资量x的平方成正比例关系,并根据市场调查与预测,得到了表格中的数据.
(1)、求证:是的切线;(2)、若 , , 求图中阴影部分的面积.22. 园林基地计划投资种植花卉及树木,已知种植树木的利润与投资量x成正比例关系,种植花卉的利润与投资量x的平方成正比例关系,并根据市场调查与预测,得到了表格中的数据.投资量x(万元)
2
种植树木利润(万元)
4
种植花卉利润(万元)
2
(1)、请根据表格填空:利润与投资量x的函数关系式为;利润与投资量x的函数关系式为;(2)、如果这个基地计划以6万元资金全部投入种植花卉和树木,设投入种植花卉的金额为m万元,种植花卉和树木共获利W万元,求出W关于m的函数关系式,并求该基地至少获得多少利润?基地能获取的最大利润是多少?(3)、若该基地想获利不低于万,在(2)的条件下,请直接写出投资种植花卉的金额m的范围.23. 已知和都是等腰三角形,且 , , 若点D在边上运动时,总保持 , 连接与交于点F . (1)、①如图1,当点D为边中点时,则的值为 ▲ ;
(1)、①如图1,当点D为边中点时,则的值为 ▲ ;②如图2,当点D不为边中点时,求证:;
(2)、如图3,当点D在边上运动中恰好使得时,若 , , 求的长.24. 如图1,抛物线与x轴相交于、两点,与y轴交于点C , 连接BC , 抛物线顶点为点M . (1)、直接写出a , b的值及点M的坐标;(2)、点N为抛物线对称轴上一点,当最小时,求点N的坐标;(3)、平移直线BC得直线 .
(1)、直接写出a , b的值及点M的坐标;(2)、点N为抛物线对称轴上一点,当最小时,求点N的坐标;(3)、平移直线BC得直线 .①如图2,若直线过点M , 交x轴于点D , 在x轴上取点 , 连接EM , 求∠DME的度数.
②把抛物线在x轴下方图象沿x轴翻折得到新图象(如图3).当直线与新图象有两个公共点时,请直接写出n的取值范围.