2024年浙教版数学八年级下册期中仿真模拟卷(三)(范围:1-4章)
试卷更新日期:2024-04-16 类型:期中考试
一、选择题(每题3分,共30分)
-
1. 下列计算正确的是( )A、 B、 C、 D、2. 方程的根是( )A、 B、 C、 D、3. 下列二次根式中,字母a的取值范围是全体实数的为 ( )A、 B、 C、 D、4. 某校在计算学生的数学学期总评成绩时,规定期中考试成绩占40%,期末考试成绩占60%.如果小林同学的数学期中考试成绩为80分,期末考试成绩为90分,那么他的数学学期总评成绩是( )A、8 0分 B、82分 C、84分 D、86分5. 在昨天的数学测试中,小明的成绩超过班级半数同学的成绩,而且在最近的三次测试中,他的成绩是最稳定的.分析得出这个结论所用的统计量应是( )A、中位数,众数 B、众数,平均数 C、平均数,方差 D、中位数,方差6. 如果关于x的一元二次方程k2x2﹣(2k+1)x+1=0有两个不相等的实数根,那么k的取值范围是( )A、 B、 且 C、 D、 且7. 如图,在Rt△ABC中,D为斜边AC的中点,E为BD上一点,F为CE的中点若AE=AD,DF=2,则BD的长为( )
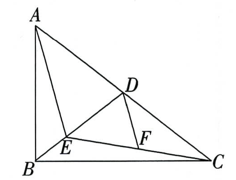 A、 B、3 C、 D、48. 如图,在平面直角坐标系xOy中,四边形ABCO是平行四边形,若A,C两点的坐标分别为(3,0),(1,2),则▱ABCO的周长为( )
A、 B、3 C、 D、48. 如图,在平面直角坐标系xOy中,四边形ABCO是平行四边形,若A,C两点的坐标分别为(3,0),(1,2),则▱ABCO的周长为( ) A、 B、 C、4 D、9. 如图,在平面直角坐标系中,▱OABC的顶点A,C分别在直线x=1和x=4上,O是坐标原点,则对角线OB长的最小值为( )
A、 B、 C、4 D、9. 如图,在平面直角坐标系中,▱OABC的顶点A,C分别在直线x=1和x=4上,O是坐标原点,则对角线OB长的最小值为( )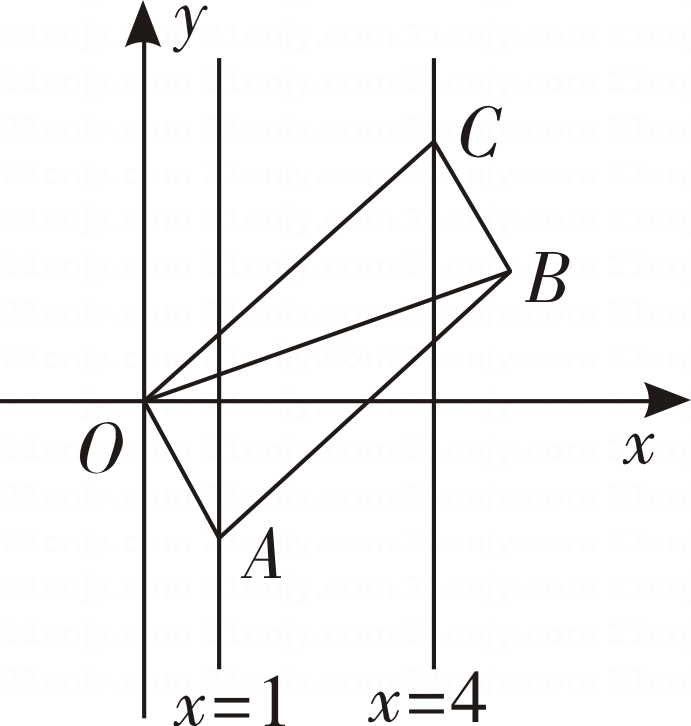 A、3 B、4 C、5 D、610. 如图,在正方形中,已知点是线段上的一个动点(点与点不重合),作交于点 . 现以 , 为邻边构造平行四边形 , 连接 , 则的最小值为( )
A、3 B、4 C、5 D、610. 如图,在正方形中,已知点是线段上的一个动点(点与点不重合),作交于点 . 现以 , 为邻边构造平行四边形 , 连接 , 则的最小值为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每题3分,共18分)
-
11. 已知 为实数, 且满足 2 , 则 的值是.12. 若一个多边形的内角和是外角和的3倍,则该多边形的边数为.13. 将方程整理成的形式为.14. 实数a,b在数轴上的位置如图所示,则化简的结果是.
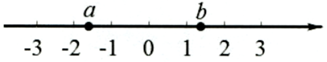 15. 如图,在Rt△ABC中,∠B=90°,BC=4,AC=5,点D在边BC上.若以AD,CD为边,AC为对角线,作▱ADCE,则对角线DE的长的最小值为.
15. 如图,在Rt△ABC中,∠B=90°,BC=4,AC=5,点D在边BC上.若以AD,CD为边,AC为对角线,作▱ADCE,则对角线DE的长的最小值为.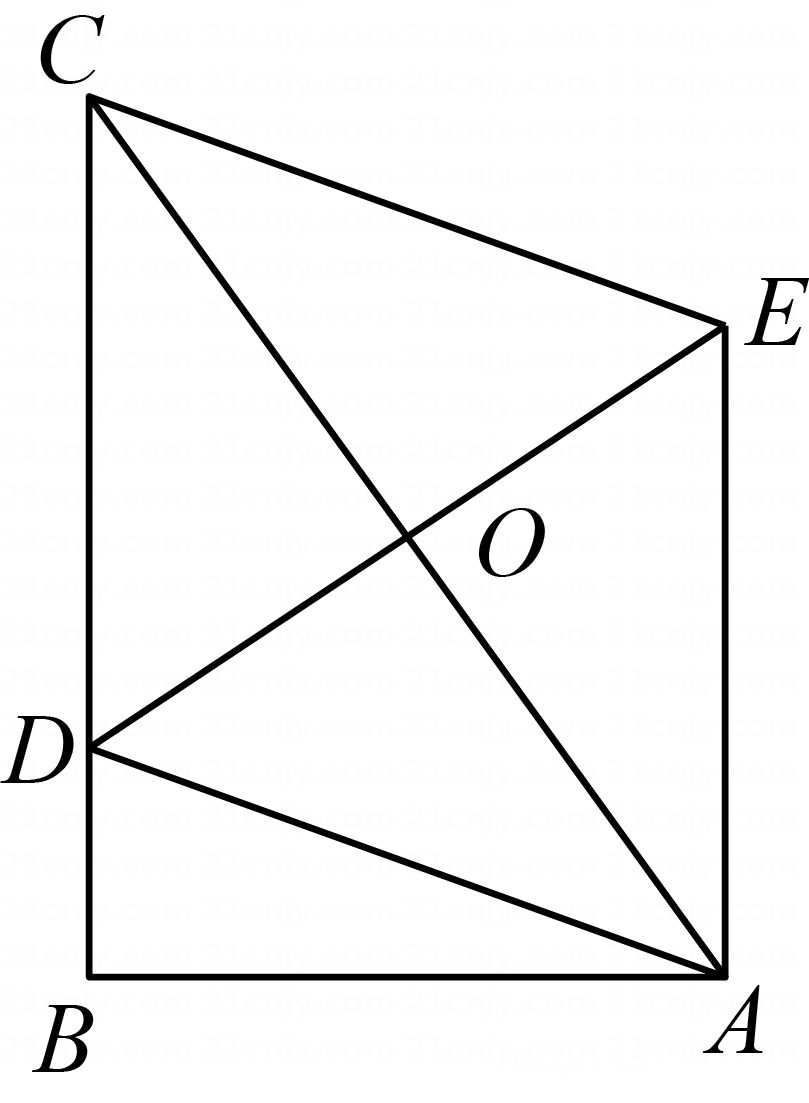 16. 把边长为2 的正方形纸片 ABCD 分割成如图所示的四块,其中点O为正方形的中心,E,F分别为AB,AD的中点.用这四块纸片拼成与此正方形不全等的四边形MNPQ(要求这四块纸片不重叠、无缝 隙),则四边形 MNPQ 的周长是
16. 把边长为2 的正方形纸片 ABCD 分割成如图所示的四块,其中点O为正方形的中心,E,F分别为AB,AD的中点.用这四块纸片拼成与此正方形不全等的四边形MNPQ(要求这四块纸片不重叠、无缝 隙),则四边形 MNPQ 的周长是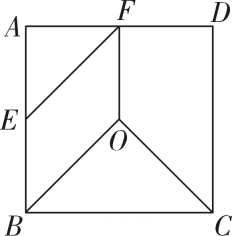
三、解答题(共8题,共72分)
-
17. 若a,b为实数,且求a+b的值.18. 已知关于x的一元二次方程 有两个不相等的实数根.求k的取值范围.19. 某学校计划利用一片空地建一个长方形学生 自行车车棚,其中一面靠墙,这堵墙的长度为12米计划建造车棚的面积为80平方米,已知现有的木板材料可使新建板墙的总长为28米.
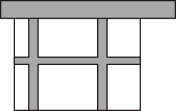 (1)、这个车棚的长和宽分别为多少米?(2)、如图,为了方便学生取车,施工单位决定在车棚内修建3条等宽的小路,使得停放自行车的面积为54平方米,那么小路的宽度是多少米?20. 挖掘问题中的隐含条件,解答下列问题:(1)、已知求x的值.(2)、已知a,b是实数,且+1,化简21. 如图,在四边形ABCD中,AC⊥BD于点E,AB=AC=BD,M为BC的中点,N为线段AM上的点,且MB=MN.
(1)、这个车棚的长和宽分别为多少米?(2)、如图,为了方便学生取车,施工单位决定在车棚内修建3条等宽的小路,使得停放自行车的面积为54平方米,那么小路的宽度是多少米?20. 挖掘问题中的隐含条件,解答下列问题:(1)、已知求x的值.(2)、已知a,b是实数,且+1,化简21. 如图,在四边形ABCD中,AC⊥BD于点E,AB=AC=BD,M为BC的中点,N为线段AM上的点,且MB=MN.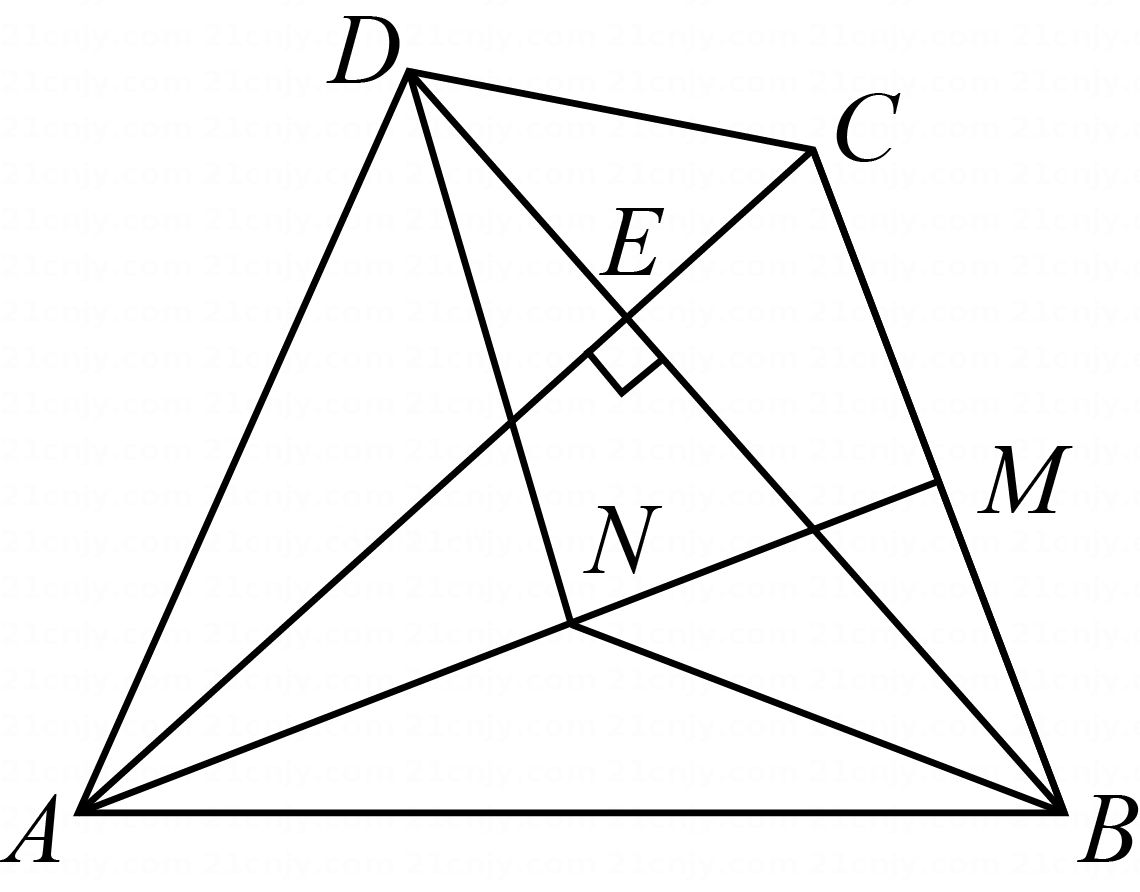 (1)、求证:BN平分∠ABE.(2)、连结DN,若BD=1,四边形DNBC为平行四边形,求线段BC的长.22. 如图,在△ABC的边BC的同侧分别作等边三角形ABD,BCF和ACE.
(1)、求证:BN平分∠ABE.(2)、连结DN,若BD=1,四边形DNBC为平行四边形,求线段BC的长.22. 如图,在△ABC的边BC的同侧分别作等边三角形ABD,BCF和ACE. (1)、证明:△ABC≌△DBF.(2)、证明:四边形AEFD是平行四边形.(3)、若AB=3,AC=4,BC=5,则∠DFE的度数为°.23. 根据以下销售情况,解决销售任务.
(1)、证明:△ABC≌△DBF.(2)、证明:四边形AEFD是平行四边形.(3)、若AB=3,AC=4,BC=5,则∠DFE的度数为°.23. 根据以下销售情况,解决销售任务.销售情况分析
总公司将一批衬衫由甲、乙两家分店共同销售,因地段不同,它们的销售情况如下:
店面
甲店
乙店
日销售情况
每天可售出20件,每件盈利40元.
每天可售出32件,每件盈利30元.
市场调查
经调查发现,每件衬衫每降价1元,甲、乙两家店一天都可多售出2件.
情况设置
设甲店每件衬衫降价元,乙店每件衬衫降价元.
任务解决
任务(1)
甲店每天的销售量 ▲ (用含的代数式表示).
乙店每天的销售量 ▲ (用含的代数式表示).
任务(2)
当时,分别求出甲、乙店每天的盈利.
任务(3)
总公司规定两家分店下降的价格必须相同,请求出每件衬衫下降多少元时,两家分店一天的盈利和为2244元.
24. 综合实践:项目主题
“亚运主题”草坪设计
项目情境
为了迎亚会,同学们参与一块长为40米,宽为30米的矩形“亚运主题”草
坪方案设计的项目学习.以下为项目学习小组对草坪设计的研究过程.
活动任务一
请设计两条相同宽度的小路连接矩形草坪两组对边.小组内同学们设计的方案主要有甲、乙、丙、丁四种典型的方案

驱动问题一
(1)项目小组设计出来的四种方案小路面积的大小关糸?
①直观猜想:我认为 ▲ ;(请用简洁的语言或代数式表达你的猜想)
②具体验证:选择最简单的甲、乙方案,假设小路宽为1米,则甲、乙方案中小路的面积分别为 ▲ 和 ▲ ;
③一般验证:若小路宽为x米,则甲、乙方案中小路所占的面积分别为 ▲ 和 ▲ .
活动任务二
为施工方便,学校选择甲种方案设计,并要求除小路后草坪面积约为1064平方米.
驱动问题二
(2)请计算两条小路的宽度是多少?
活动任务三
为了布置五环标志等亚运元素,将在草坪上的亚运宣传主题墙前,用篱笆围(三边)成面积为100平方米的矩形 , 如图.
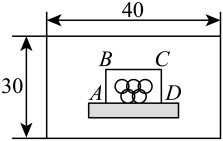
驱动问题三
(3)为了使篱笆恰好用完同时围住三面,项目小组的同学对下列问题展开探究,其中矩形宽 , 长 .
①若30米长的篱笆,请用两种不同的函数表示y关于x的函数关系.
②数学之星小明提出一个问题:若a米长的篱笆恰好用完,且有两种不同方案可以选择,使得两种方案的宽之和小于15米,甲同学说“篱笆的长可以是28米”,乙同学说“篱笆的长可以是32米”,你认为他们俩的说法对吗?请说明理由.