2024年北师大版数学八(下)期中专项复习8 简单的图案设计
试卷更新日期:2024-04-16 类型:复习试卷
一、选择题
-
1. 下列图形中可以由一个基础图形通过平移变换得到的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下图中所给图形只用平移可以得到的是( )A、
2. 下图中所给图形只用平移可以得到的是( )A、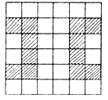 B、
B、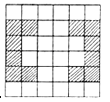 C、
C、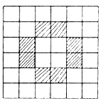 D、
D、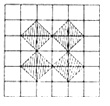 3.
3.2012年10月8日,江西省第三届花卉园艺博览交易会在宜春花博园隆重开幕,此届花博会的吉祥物的名字叫“迎春”(如图).通过平移,可将图中的“迎春”平移到图( )
 A、
A、 B、
B、 C、
C、 D、
D、 4. 图案※○※○※○※○※○※○可以由一组“基本图案”平移复制后得到,这个基本图案不能是( )A、※○ B、※○※ C、※○※○ D、※○※○※○5. 下列图案可以看作某一部分平移后得到的是( )A、
4. 图案※○※○※○※○※○※○可以由一组“基本图案”平移复制后得到,这个基本图案不能是( )A、※○ B、※○※ C、※○※○ D、※○※○※○5. 下列图案可以看作某一部分平移后得到的是( )A、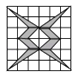 B、
B、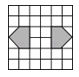 C、
C、 D、
D、 6. 下列四个图案,可看成由图案自身的一部分平移后得到的是( )A、
6. 下列四个图案,可看成由图案自身的一部分平移后得到的是( )A、 B、
B、 C、
C、 D、
D、 7.
7.如图是一个镶边的模板,它的内部是由下列哪个“基本图案”通过一次平移得到的( )
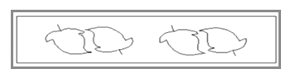 A、
A、 B、
B、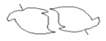 C、
C、 D、
D、 8.
8.欣赏并说出下列各商标图案,是利用平移来设计的有( )
 A、2个 B、3个 C、5个 D、6个9. 下列四组图形中,有一组中的两个图形经过平移其中一个,能得到另一个,这组是( )A、
A、2个 B、3个 C、5个 D、6个9. 下列四组图形中,有一组中的两个图形经过平移其中一个,能得到另一个,这组是( )A、 B、
B、 C、
C、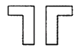 D、
D、 10.
10.如下图所给的图形中只用平移可以得到的有( )
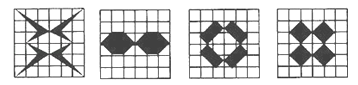 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 观察图1和图2,请回答下列问题:
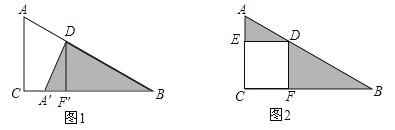
(1)请简述由图1变成图2的形成过程: .
(2)若AD=3,DB=4,则△ADE和△BDF面积的和为 .
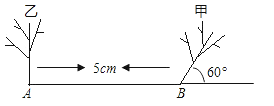
12.如图,甲图怎样变成乙图: .
 13.
13.在平移、位似、旋转、轴对称四种图形变换中,如图图案中不包含的变换的是 .
 14.
14.如图,正方形ABCD可以看作由什么“基本图形”经过怎样的变化形成的? .
 15. 在图形的平移、旋转、轴对称变换中,其相同的性质是 .
15. 在图形的平移、旋转、轴对称变换中,其相同的性质是 .三、作图题
-
16.
在下图方框中设计一个美丽的中心对称图形并使它成为正方体的一种侧面展开图 .

四、解答题
-
17.
如图②是4×4网格,每个小正方形的边长都为1,请用图案①作为基本图案,通过平移,轴对称,旋转变换,设计两个不同的精美图案,使它们满足:①既是轴对称图形,又是中心对称图形;②所作图案用阴影标识,且阴影部分面积为4.
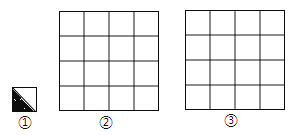 18.
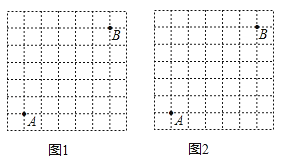
18.图1、图2分别是7×7的正方形网格,网格中每个小正方形的边长均为1,点A、B在小正方形的顶点上.
(1)在图1中确定点C、D(点C、D在小正方形的顶点上),并画出以A、B、C、D为顶点的四边形,使其是中心对称图形,但不是轴对称图形,且面积为15;
(2)在图2中确定点E、F(点E、F在小正方形的顶点上),并画出以A、B、E、F为顶点的四边形,使其既是轴对称图形,又是中心对称图形,且面积为15.
 19.
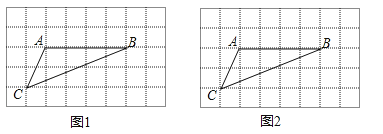
19.如图,在8×5的正方形网格中,每个小正方形的边长均为1,△ABC的三个顶点均在小正方形的顶点上.
(1)在图1中画△ABD(点D在小正方形的顶点上),使△ABD的周长等于△ABC的周长,且以A、B、C、D为顶点的四边形是轴对称图形.
(2)在图2中画△ABE(点E在小正方形的顶点上),使△ABE的周长等于△ABC的周长,且以A、B、C、E为顶点的四边形是中心对称图形,并直接写出该四边形的面积.
 20.
20.(1)请写出是旋转对称图形的两种多边形(正三角形除外)的名称,并分别写出其旋转角α的最小值;
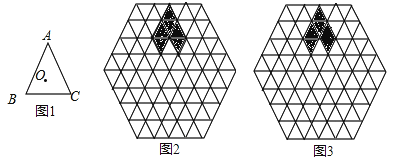
(2)下面的网格图都是由边长为1的正三角形组成的,请以图中给出的图案为基本图形(其顶点均在格点上),在图2、图3中再分别添加若干个基本图形,使添加的图形与原基本图形组成一个新图案,要求:
①图2中设计的图案既是旋转对称图形又是轴对称图形;
②图3中设计的图案是旋转对称图形,但不是中心对称图形;
③所设计的图案顶点都在格点上,并给图案上阴影(建议用一组平行线段表示阴影).
 21.
21.在数学活动课上,王老师发给每位同学一张半径为6个单位长度的圆形纸板,要求同学们:
(1)从带刻度的三角板、量角器和圆规三种作图工具中任意选取作图工具,把圆形纸板分成面积相等的四部分;
(2)设计的整个图案是某种对称图形.
王老师给出了方案一,请你用所学的知识再设计两种方案,并完成下面的设计报告.
名 称
四等分圆的面积
方 案
方案一
方案二
方案三
选用的工具
带刻度的三角板
画出示意图
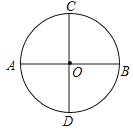


简述设计方案
作⊙O两条互相垂直的直径AB、CD,将⊙O的面积分成相等的四份.
指出对称性
既是轴对称图形又是中心对称图形
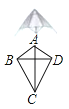
22. 阅读以下材料,并按要求完成相应的任务.几何中,平行四边形、矩形、菱形、正方形和等腰梯形都是特殊的四边形,大家对于它们的性质都非常熟悉,生活中还有一种特殊的四边形﹣﹣筝形.所谓筝形,它的形状与我们生活中风筝的骨架相似.
定义:两组邻边分别相等的四边形,称之为筝形,如图,四边形ABCD是筝形,其中AB=AD,CB=CD
判定:①两组邻边分别相等的四边形是筝形
②有一条对角线垂直平分另一条对角线的四边形是筝形
显然,菱形是特殊的筝形,就一般筝形而言,它与菱形有许多相同点和不同点
如果只研究一般的筝形(不包括菱形),请根据以上材料完成下列任务:
(1)请说出筝形和菱形的相同点和不同点各两条;
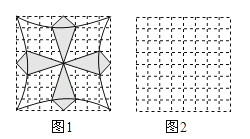
(2)请仿照图1的画法,在图2所示的8×8网格中重新设计一个由四个全等的筝形和四个全等的菱形组成的新图案,具体要求如下:
①顶点都在格点上;
②所设计的图案既是轴对称图形又是中心对称图形;
③将新图案中的四个筝形都涂上阴影(建议用一系列平行斜线表示阴影).
-