2024年北师大版数学八(下)期中专项复习7 图形的旋转与中心对称
试卷更新日期:2024-04-16 类型:复习试卷
一、选择题
-
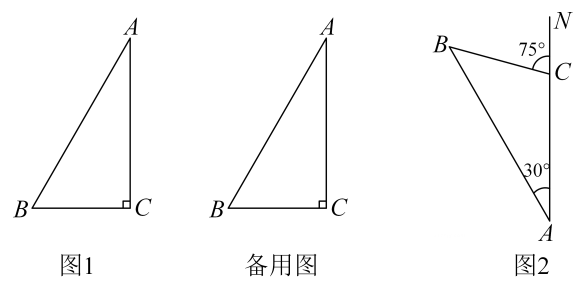
1. 把图中的五角星图案,绕着它的中心点进行旋转,若旋转后与自身重合,则至少旋转( )
 A、 B、 C、 D、2. 下列图形中,是中心对称图形的是( )A、等腰三角形 B、等边三角形 C、正方形 D、直角三角形3. 如图,一个小孩坐在秋千上,若秋千绕点O旋转了80°,小孩的位置也从A点运动到了B点,则∠OAB的度数为 ( )
A、 B、 C、 D、2. 下列图形中,是中心对称图形的是( )A、等腰三角形 B、等边三角形 C、正方形 D、直角三角形3. 如图,一个小孩坐在秋千上,若秋千绕点O旋转了80°,小孩的位置也从A点运动到了B点,则∠OAB的度数为 ( ) A、70° B、60° C、50° D、40°4. 下列图形是中心对称图形,但不是轴对称图形的是( )A、
A、70° B、60° C、50° D、40°4. 下列图形是中心对称图形,但不是轴对称图形的是( )A、 B、
B、 C、
C、 D、
D、 5. 如图,要使此图形旋转后与自身重合,至少应将它绕中心旋转的度数为( )
5. 如图,要使此图形旋转后与自身重合,至少应将它绕中心旋转的度数为( ) A、 B、 C、 D、6. 如图,为正方形内一点, , 将绕点逆时针旋转得到 , 则的长是( )
A、 B、 C、 D、6. 如图,为正方形内一点, , 将绕点逆时针旋转得到 , 则的长是( )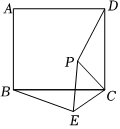 A、 B、 C、 D、7. 下列图形中,既是中心对称图形又是轴对称图形的是( )A、
A、 B、 C、 D、7. 下列图形中,既是中心对称图形又是轴对称图形的是( )A、 B、
B、 C、
C、 D、
D、 8. 如图,是正内的一点,若将绕点旋转到 , 则的度数是( )
8. 如图,是正内的一点,若将绕点旋转到 , 则的度数是( )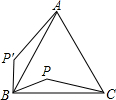 A、 B、 C、 D、9. 教育部门高度重视校园安全教育,要求各级各类学校从认识安全警告标志入手开展安全教育.下列安全图标是中心对称图形的是( )A、注意安全
A、 B、 C、 D、9. 教育部门高度重视校园安全教育,要求各级各类学校从认识安全警告标志入手开展安全教育.下列安全图标是中心对称图形的是( )A、注意安全 B、急救中心
B、急救中心 C、水深危险
C、水深危险 D、禁止攀爬
D、禁止攀爬 10. 如图,在中, , , 为的中点,将绕点按顺时针方向旋转得到 , 使点落在边上,点落在的延长线上,连接 , , , 若 , 则下列结论错误的是( )
10. 如图,在中, , , 为的中点,将绕点按顺时针方向旋转得到 , 使点落在边上,点落在的延长线上,连接 , , , 若 , 则下列结论错误的是( )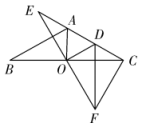 A、 B、 C、是等边三角形 D、垂直平分
A、 B、 C、是等边三角形 D、垂直平分二、填空题
-
11. 如图,绕点逆时针旋转得到 , 则 .
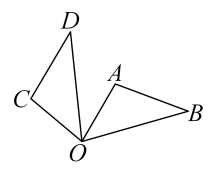 12. 如图,一个含有30°角的三角板ABC,绕点B顺时针旋转到的位置,使A,B,在同一条直线上,则旋转角的度数为.
12. 如图,一个含有30°角的三角板ABC,绕点B顺时针旋转到的位置,使A,B,在同一条直线上,则旋转角的度数为.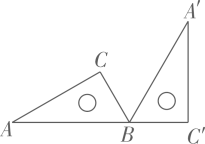 13. 如图,在中, , , 将绕点逆时针方向旋转到的位置,则图中阴影部分的面积是 .
13. 如图,在中, , , 将绕点逆时针方向旋转到的位置,则图中阴影部分的面积是 .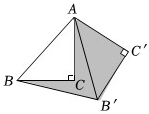 14. 如图,在中, , , , 点P为边上任意一点,连接 , 以C为中心将按逆时针方向旋转得 , 连接 , 则的最小值为 .
14. 如图,在中, , , , 点P为边上任意一点,连接 , 以C为中心将按逆时针方向旋转得 , 连接 , 则的最小值为 .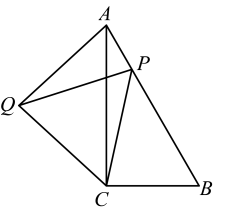 15. 如图,等边三角形绕点旋转到的位置,且则旋转了度.
15. 如图,等边三角形绕点旋转到的位置,且则旋转了度.
三、作图题
-
16. 如图,平面直角坐标系内,小正方形网格的边长为1个单位长度,△ABC的顶点均在格点上.
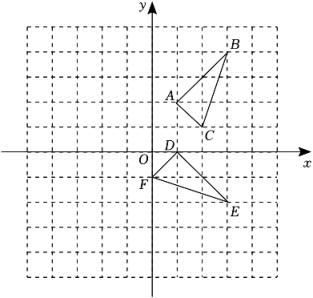 (1)、画出将△ABC关于原点O的中心对称图形△A1B1C1;(2)、将△DEF绕点E逆时针旋转90°得到△D1EF1 , 画出△D1EF1;(3)、若△DEF由△ABC绕着某点旋转得到的,则这点的坐标为 .17. 如图,在平面直角坐标中,的顶点坐标分别是 .
(1)、画出将△ABC关于原点O的中心对称图形△A1B1C1;(2)、将△DEF绕点E逆时针旋转90°得到△D1EF1 , 画出△D1EF1;(3)、若△DEF由△ABC绕着某点旋转得到的,则这点的坐标为 .17. 如图,在平面直角坐标中,的顶点坐标分别是 .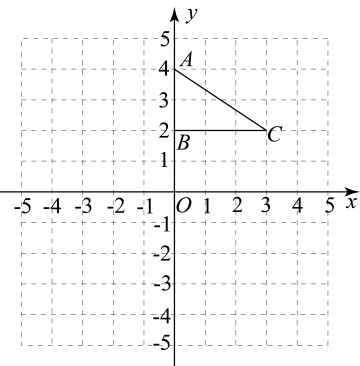 (1)、将以O为旋转中心旋转 , 画出旋转后对应的;(2)、将平移后得到 , 若点A的对应点的坐标为 , 画出平移后对应的;(3)、求线段的长度.18. 如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点(顶点是网格线的交点).
(1)、将以O为旋转中心旋转 , 画出旋转后对应的;(2)、将平移后得到 , 若点A的对应点的坐标为 , 画出平移后对应的;(3)、求线段的长度.18. 如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点(顶点是网格线的交点).
( 1 )先将竖直向上平移6个单位,再水平向右平移1个单位得到 , 请画出;
( 2 )将绕点顺时针旋转 , 得 , 请画出;
( 3 )求(2)中点旋转到点所经过的弧长(结果保留π).
四、解答题
-
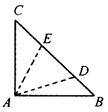
19. 如图所示,在Rt△ABC中,∠BAC=90°,AC=AB,∠DAE=45°,且BD=3,CE=4 ,求DE的长.
 20. 如图,在Rt△ABC中,∠ACB=90°,点D,E分别在AB,AC上,CE=BC,连接CD,将线段CD绕点C按顺时针方向旋转90°后得CF,连接EF. 若EF∥CD,求证:∠BDC=90°.
20. 如图,在Rt△ABC中,∠ACB=90°,点D,E分别在AB,AC上,CE=BC,连接CD,将线段CD绕点C按顺时针方向旋转90°后得CF,连接EF. 若EF∥CD,求证:∠BDC=90°.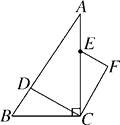 21.
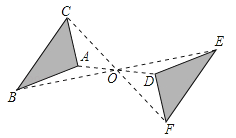
21.如图,△ABC与△DEF关于点O对称,请你写出两个三角形中的对称点,相等的线段,相等的角.
五、实践探究题