2024年浙教版数学八年级下册期中仿真模拟卷（一）（范围：1-3章）

试卷更新日期：2024-04-16 类型：期中考试

进入出卷网下载

一、选择题（每题3分，共30分）

1. 下列各式中，一定是二次根式的是（）

A、 $\sqrt{a}$ B、 $\sqrt{- 2}$ C、 $\sqrt{- 4^{2}}$ D、 $\sqrt{(- 3)^{2}}$

查看试题解析
2. $\sqrt{5}$ 的倒数是（）

A、 $\frac{\sqrt{5}}{5}$ B、 $- \frac{\sqrt{5}}{5}$ C、 $- \sqrt{5}$ D、 $\sqrt{5}$

查看试题解析
3. 如图，网格小正方形边长为3， $△ A B C$ 的三个顶点均在网格的格点上，中线 $A E ， B F$ 的交点为O，则 $C O$ 的长度为（）

A、 $3 \sqrt{17}$ B、 $\frac{2}{3} \sqrt{17}$ C、 $2 \sqrt{26}$ D、 $\sqrt{26}$

查看试题解析
4. 已知一组样本数据 $x_{1}, x_{2}, \cdot \cdot \cdot, x_{n}$ 为不全相等的 $n$ 个正数，其中 $n ⩾ 4$ .若把数据 $x_{1}, x_{2}, \cdot \cdot \cdot, x_{n}$ 都扩大 $m$ 倍再减去 $l$ （其中 $m$ 是实数， $l \neq 0$ ），生成一组新的数据 $m x_{1} - l, m x_{2} - l, \cdot \cdot \cdot, m x_{n} - l$ ，则这组新数据与原数据相比较，（）

A、平均数相等 B、中位数相等 C、方差相等 D、标准差可能相等

查看试题解析
5. 在一次中考体育模拟测试中，某班41名学生参加测试（满分为30分），成绩统计如表，部分数据被遮盖，下列统计量中，与被遮盖的数据无关的是（）
成绩（分）
22
24
26
27
28
29
30
人数（人）
▆
▆
2
6
19
▆
7

A、平均数、众数 B、平均数、方差 C、中位数、众数 D、中位数、方差

查看试题解析
6. 对于任意的正实数m，n，定义运算“※”：m※n= $\{\begin{array}{l} \sqrt{m} - \sqrt{n} (m \geq n)， \\ \sqrt{m} + \sqrt{n} (m < n)， \end{array}$ 计算(3※2)×(8※12)的结果为(　　)

A、2-4 $\sqrt{6}$ B、2 C、2 $\sqrt{5}$ D、20

查看试题解析
7. 已知关于x的方程 $x^{2} - k x - 6 = 0$ 的一个根为 $x = 3$ ，则实数k的值为（）

A、1 B、 $- 1$ C、2 D、 $- 2$

查看试题解析
8. 如果关于x的方程. $x^{2} + 2 (m - 1) x + m^{2} - m = 0$ 有两个实数根α，β，且 $a^{2} + β^{3} = 12 ，$ 那么m的值为（）

A、-1 B、-4 C、-4或1 D、-1或4

查看试题解析
9. 为了宣传环保，某学生写了一份倡议书在微博传播，规则为：将倡议书发表在自己的微博，再邀请n个好友转发倡议书，每个好友转发倡议书，又邀请n个互不相同的好友转发倡议书，以此类推，已知经过两轮传播后，共有1641人参与了传播活动，则方程列为（）

A、(n+1)²=1641 B、(n- 1)²=1641 C、n(n+1)=1641 D、1+n+n²=1641

查看试题解析
10. 关于 $x$ 的一元二次方程 $a x^{2} + b x + c = 0 (a \neq 0)$ ，下列说法中：
①若 $a - b + c = 0$ ，则 $b^{2} - 4 a c \geq 0$ ；
②若方程 $a x^{2} + c = 0$ 有两个不相等的实根，则方程 $a x^{2} + b x + c = 0$ 必有两个不相等的实根；
③若 $c$ 是方程 $a x^{2} + b x + c = 0$ 的一个根，则一定有 $a c + b + 1 = 0$ 成立；
④若 $x_{0}$ 是一元二次方程 $a x^{2} + b x + c = 0$ 的根，则 $b^{2} - 4 a c = {(2 a x_{0} + b)}^{2}$
其中正确的：（）

A、只有① B、只有①② C、只有①②③ D、只有①②④

查看试题解析

成绩（分）	22	24	26	27	28	29	30
人数（人）	▆	▆	2	6	19	▆	7

二、填空题（每题3分，共18分）

11. 甲、乙两名同学的5次射击训练成绩(单位：环)如下表所示：
甲
7
8
9
8
8
乙
6
10
9
7
8
比较甲、乙这5次射击成绩的方差 $S_{甲}^{2} ， S_{乙}^{2}$ ，结果为 $S_{甲}^{2}$ $S_{乙}^{2}$ (填“>”“<”或“=”).

查看试题解析
12. 小云和小天练习射击，一轮10发子弹打完后，两人的成绩如图所示.根据图中的信息，小云和小天两人中成绩较稳定的是.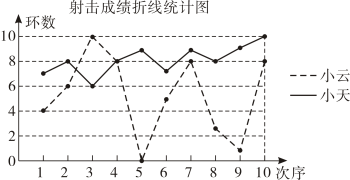

查看试题解析
13. 工人师傅准备在一块长为60，宽为48的长方形花圃内修建四条宽度相等，且与各边垂直的小路．四条小路围成的中间部分恰好是一个正方形，且边长是小路宽度的8倍．若四条小路所占面积为160．设小路的宽度为x，依题意列方程，化为一般形式为．

查看试题解析
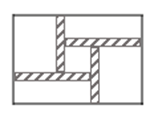14. 一家鞋店对上周某一品牌女鞋的销售量进行统计后，决定本周进该品牌女鞋时，多进一些尺码为23.5cm的鞋，影响鞋店决策的统计量是.

查看试题解析
15. 下表是小红参加一次“阳光体育”活动比赛的得分情况：
项目
跑步
花样跳绳
跳绳
得分
90
80
70
评总分时，按跑步占50%，花样跳绳占30%，跳绳占20%考评，则小红的最终得分为分.

查看试题解析
16. 如图①是一张等腰直角三角形纸片， $A C = B C = 20 \sqrt{2} c m$ ，现要求按照图②的方法裁剪几条宽度都为 $5 \sqrt{2} c m$ 的长方形纸条，用这些纸条为一幅正方形美术作品EFGH镶边(纸条不重叠)如图③，正方形美术作品的面积为 $c m^{2}$ .

查看试题解析

三、解答题（共8题，共72分）

17. 计算：

(1)、 $(2 \sqrt{12} - 3 \sqrt{\frac{1}{3}}) \times \sqrt{6} .$

(2)、 $(\sqrt{3} - \sqrt{2}) (\sqrt{3} + \sqrt{2}) + \frac{2 \sqrt{12} + \sqrt{3}}{3} + {(\frac{1}{6})}^{- 1} .$

查看试题解析
18. 七年级某班的教室里，一位同学的五次数学成绩分别是：62，62，98，99，100．其中它的中位数，众数，平均数分别是多少？

查看试题解析
19. 若a，b为实数，且b= $\frac{\sqrt{a^{2} - 1} + \sqrt{1 - a^{2}} + a}{a + 1}$ ， $\sqrt{c^{2}}$ =a+3，求ab+c的值

查看试题解析
20. 有一块长方形木板，木工采用如图所示的方式，在木板上截出两个面积分别为18dm² 和32dm²的正方形木板.

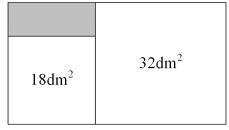(1)、求剩余木板的面积.

(2)、若木工想从剩余的木板中截出长为 1.5d m、宽为 1 dm的长方形木条，则最多能截出块.

查看试题解析
21. 某校学生会要在甲、乙两位候选人中选择一人担任文艺部干事，对他们进行了文化水平艺术水平组织能力的测试，根据综合成绩择优录取，他们的各项成绩(单项满分100分)如下表所示：
候选人
文化水平
艺术水平
组织能力
甲
80分
87分
82分
乙
80分
96分
76分

(1)、如果把各项成绩的平均数作为综合成绩，应该录取谁？

(2)、如果想录取一名组织能力较强的候选人，把文化水平、艺术水平、组织能力三项成绩分别按照20%，20%，60%的比例计人综合成绩，应该录取谁？

查看试题解析
22. 观察下列各式并解答问题：
$\sqrt{1 + \frac{1}{1^{2}} + \frac{1}{2^{2}}} = 1 + \frac{1}{1} - \frac{1}{2} = 1 \frac{1}{2}$ ；
$\sqrt{1 + \frac{1}{2^{2}} + \frac{1}{3^{2}}} = 1 + \frac{1}{2} - \frac{1}{3} = 1 \frac{1}{6}$ ；
$\sqrt{1 + \frac{1}{3^{2}} + \frac{1}{4^{2}}} = 1 + \frac{1}{3} - \frac{1}{4} = 1 \frac{1}{12}$ .

(1)、请你按照上面每个等式反映的规律，写出用n(n为正整数)表示的等式：。

(2)、利用上述规律计算 $\sqrt{\frac{50}{49} + \frac{1}{64}}$

(3)、已知 $\sqrt{1 + \frac{1}{1^{2}} + \frac{1}{2^{2}}} + \sqrt{1 + \frac{1}{2^{2}} + \frac{1}{3^{2}}} + \dots + \sqrt{1 + \frac{1}{(n - 2)^{2}} + \frac{1}{(n - 1)^{2}}} + \sqrt{1 + \frac{1}{(n - 1)^{2}} + \frac{1}{n^{2}}} = n - \frac{1}{2023}$ ，求n的值.

查看试题解析
23. 材料一：我们在学习二次根式的过程中，若遇到 $\frac{1}{2 + \sqrt{3}}$ 这种形式的式子，可以通过分子、分母同乘分母的有理化因式，将分母化为有理数，如 $\frac{1}{2 + \sqrt{3}} = \frac{2 - \sqrt{3}}{(2 + \sqrt{3}) (2 - \sqrt{3})} = \frac{2 - \sqrt{3}}{4 - 3} = 2 - \sqrt{3}$ ．这个过程叫做“分母有理化”。

(1)、已知a= $\frac{1}{3 - 2 \sqrt{2}}$ ， b= $\frac{1}{3 + 2 \sqrt{2}}$ ，求a+b的值．

(2)、材料二：有一个类似的方法叫做“分子有理化”：分母和分子都乘分子的有理化因式，从而消掉分子中的根式，如 $\frac{\sqrt{5} - 2}{2} = \frac{(\sqrt{5} - 2) (\sqrt{5} + 2)}{2 (\sqrt{5} + 2)} = \frac{1}{2 (\sqrt{5} + 2)}$ ．利用这两种有理化的方式，我们可以处理一些二次根式的比较和求值问题：
比较下列各组数的大小：
① $\frac{1}{\sqrt{7} - \sqrt{6}}$ 和 $\frac{1}{\sqrt{6} - \sqrt{5}}$
② $3 \sqrt{2} - 4$ 和 $2 \sqrt{3} - \sqrt{10}$

(3)、求y= $\frac{\sqrt{1 + x} - \sqrt{x}}{3}$ 的最大值．

查看试题解析
24. 如图，在长方形ABCD中，AB=6cm，AD=2cm，点P以2cm/s的速度从顶点A出发沿折线A→B→C向点C运动，同时点Q以1cm/s的速度从顶点C出发沿边CD向点D运动．当其中一个动点到达末端停止运动时，另一点也停止运动．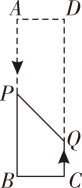

(1)、当四边形PBCQ的面积是长方形ABCD面积的 $\frac{4}{9}$ 时，求出两动点的运动时间t．

(2)、是否存在某一时刻，点P与点Q之间的距离为 $\sqrt{5}$ cm？若存在，则求出运动所需的时间；若不存在，请说明理由．

查看试题解析

候选人	文化水平	艺术水平	组织能力
甲	80分	87分	82分
乙	80分	96分	76分

项目	跑步	花样跳绳	跳绳
得分	90	80	70