2024年浙教版数学七年级下册期中仿真模拟卷(三)(范围:1-4章)
试卷更新日期:2024-04-16 类型:期中考试
一、选择题(每题3分,共30分)
-
1. 下列方程中,属于二元一次方程的是( )A、6x-2z=5y B、 C、x2-3y=1 D、x-2y=32. 多项式(x+1)2-9因式分解的结果为( )A、(x+8)(x+1) B、(x-2)(x+4) C、(x-4)(x+2) D、(x-10)(x+8)3. 下列结论正确的是( )A、过一点有且只有一条直线与已知直线垂直 B、过一点有且只有一条直线与已知直线平行 C、在同一平面内,不相交的两条射线是平行线 D、如果两条直线都与第三条直线平行,那么这两条直线互相平行4. 若关于x,y的方程组的解互为相反数,则k的值为( )A、4 B、2 C、-1 D、-55. 已知M=8x2-y2+6x-2,N=9x2+4y+13,则M-N的值为( )A、正数 B、负数 C、非正数 D、不能确定6. 如图,直线AB∥CD,DE⊥BC于点E,若∠CDE=57°,则∠1的度数是( )
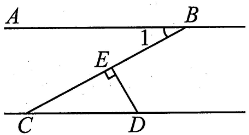 A、57° B、33° C、23° D、47°7. 为了绿化校园,30名学生共种78棵树苗,其中男生每人种3棵,女生每人种2棵.设男生有工人,女生有y人,根据题意,所列方程组正确的是( )A、 B、 C、 D、8. 某同学在研究传统文化“抖空竹”时有一个发现:他把它抽象成数学问题,如图,已知AB∥CD,∠BAE=88°,∠DCE=126°,则∠E的度数是( )
A、57° B、33° C、23° D、47°7. 为了绿化校园,30名学生共种78棵树苗,其中男生每人种3棵,女生每人种2棵.设男生有工人,女生有y人,根据题意,所列方程组正确的是( )A、 B、 C、 D、8. 某同学在研究传统文化“抖空竹”时有一个发现:他把它抽象成数学问题,如图,已知AB∥CD,∠BAE=88°,∠DCE=126°,则∠E的度数是( ) A、28° B、38° C、48° D、589. 如图,AB∥CD,将一副直角三角尺按如图摆放,∠GEF=60°,∠MNP=45°。有下列结论:①GE∥MP;②∠EFN=150°;③∠BEF=75°;④∠AEG=∠PMN。其中正确的个数是( )
A、28° B、38° C、48° D、589. 如图,AB∥CD,将一副直角三角尺按如图摆放,∠GEF=60°,∠MNP=45°。有下列结论:①GE∥MP;②∠EFN=150°;③∠BEF=75°;④∠AEG=∠PMN。其中正确的个数是( ) A、1 B、2 C、3 D、410. 如图,AB∥CD,E为AB上方一点,FB,CG分别平分∠EFG,∠ECD.若∠E+2∠G=210°,则∠EFG的度数为( )
A、1 B、2 C、3 D、410. 如图,AB∥CD,E为AB上方一点,FB,CG分别平分∠EFG,∠ECD.若∠E+2∠G=210°,则∠EFG的度数为( )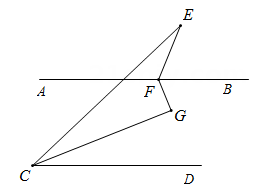 A、130° B、140° C、150° D、160°
A、130° B、140° C、150° D、160°二、填空题(每题3分,共18分)
-
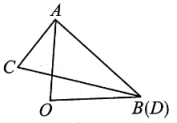
11. 。12. 一副三角尺按如图所示叠放在一起,其中点 B,D重合,若固定三角形 AOB,改变三角尺ACD的位置(其中 A 点位置始终不变),当∠BAD= 时,CD∥AB。
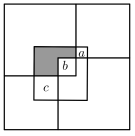
 13. 若关于的方程组的解之和为3,则的值为 .14. 如图,把三个大小相同的正方形放在边长为7的大正方形中,重叠部分的正方形面积分别记为a和c,延长线构成的正方形面积记为b,若 , 且 , 则图中阴影部分面积的值为 .
13. 若关于的方程组的解之和为3,则的值为 .14. 如图,把三个大小相同的正方形放在边长为7的大正方形中,重叠部分的正方形面积分别记为a和c,延长线构成的正方形面积记为b,若 , 且 , 则图中阴影部分面积的值为 .
 15. 若 , 且 , 则代数式的值为 .16. 有一副直角三角板和 , 其中 , , 如图所示叠放,边点边交于点 , 过点作平分 , 若 , 则度.
15. 若 , 且 , 则代数式的值为 .16. 有一副直角三角板和 , 其中 , , 如图所示叠放,边点边交于点 , 过点作平分 , 若 , 则度.
三、解答题(共8题,共72分)
-
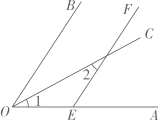
17. 解下列方程组:(1)、(2)、18. 先化简.再求值:(2a+b)2-2(a-2b) (2a+b)的值,其中a4=4b=16,,且ab<0·19. 如图,OC是∠AOB的平分线,且∠1=∠2,试说明EF∥OB的理由.
 20. 甲、乙两名同学在解方程组时,甲同学因看错了 , 从而求得解为 , 乙同学因看错了 , 从而球得解为 , 计算 , 并用幂的形式表示结果.21. 某商店3月份购进一批T恤衫,进价合计12万元,因畅销,商店又于4月份购进一批同品牌T恤衫,进价合计15万元,数量是3月份的1.2倍,但每件进价涨了5元.(1)、3月份购进的T恤衫的单价是多少?4月份购进了多少件T恤衫?(2)、这两批T恤衫开始都以每件180元出售,结果4月份后期出现滞销,还有一半的T恤衫没有售出,于是5月份商店便以定价的n折开始销售(n是正整数,且1≤n≤9),结果第二批T恤衫共盈利800m元(m为正整数).求m,n的值.22. 某地汛期来临,防汛指挥部在一危险地带两岸各安置了一探照灯,便于夜间查看江水及两岸河堤的情况.如图1,灯A射线自顺时针旋转至便立即回转,灯B射线自顺时针旋转至便立即回转,两灯不停交叉照射巡视.若灯A转动的速度是秒,灯B转动的速度是秒,且a , b满足 . 假定这一带江堤是平行的,即 , 且 .
20. 甲、乙两名同学在解方程组时,甲同学因看错了 , 从而求得解为 , 乙同学因看错了 , 从而球得解为 , 计算 , 并用幂的形式表示结果.21. 某商店3月份购进一批T恤衫,进价合计12万元,因畅销,商店又于4月份购进一批同品牌T恤衫,进价合计15万元,数量是3月份的1.2倍,但每件进价涨了5元.(1)、3月份购进的T恤衫的单价是多少?4月份购进了多少件T恤衫?(2)、这两批T恤衫开始都以每件180元出售,结果4月份后期出现滞销,还有一半的T恤衫没有售出,于是5月份商店便以定价的n折开始销售(n是正整数,且1≤n≤9),结果第二批T恤衫共盈利800m元(m为正整数).求m,n的值.22. 某地汛期来临,防汛指挥部在一危险地带两岸各安置了一探照灯,便于夜间查看江水及两岸河堤的情况.如图1,灯A射线自顺时针旋转至便立即回转,灯B射线自顺时针旋转至便立即回转,两灯不停交叉照射巡视.若灯A转动的速度是秒,灯B转动的速度是秒,且a , b满足 . 假定这一带江堤是平行的,即 , 且 .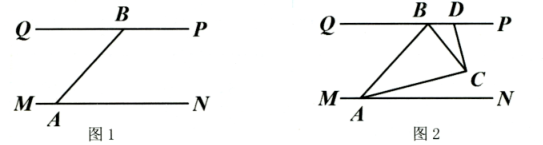 (1)、求a , b的值.(2)、若灯B射线先转动30秒,灯A射线才开始转动,在灯B射线到达之前,灯A转动几秒,两灯的光束互相平行?(3)、如图2,两灯同时转动,在灯A射线到达之前,若两灯射出的光束相交于点C , 过点C作 , 交于点D , 则在转动过程中,的值是否发生变化?若不变,请求出该值;若改变,请求出其取值范围.23. 对于未知数为x,y的二元一次方程组,如果方程组的解x,y满足|x-y|=1,我们就说方程组的解x与y具有“邻好关系”.(1)、方程组的解x与y(项“具有”或“不具有”)“邻好关系”;(2)、若方程组的解x与y具有“邻好关系”,求m的值;(3)、未知数为x,y的方程组 , 其中a与x,y都是正整数,该方程组的解x与y是否具有“邻好关系”?如果具有,请求出a的值及方程组的解;如果不具有,请说明理由.(4)、【拓展】若一个关于x的方程ax+b=0(a≠0)的解为x=b-a,则称之为“成章方程”.如:x+=0的解为x=- , 而-=-1;2x+=0的解为x=- , 而-=-2.
(1)、求a , b的值.(2)、若灯B射线先转动30秒,灯A射线才开始转动,在灯B射线到达之前,灯A转动几秒,两灯的光束互相平行?(3)、如图2,两灯同时转动,在灯A射线到达之前,若两灯射出的光束相交于点C , 过点C作 , 交于点D , 则在转动过程中,的值是否发生变化?若不变,请求出该值;若改变,请求出其取值范围.23. 对于未知数为x,y的二元一次方程组,如果方程组的解x,y满足|x-y|=1,我们就说方程组的解x与y具有“邻好关系”.(1)、方程组的解x与y(项“具有”或“不具有”)“邻好关系”;(2)、若方程组的解x与y具有“邻好关系”,求m的值;(3)、未知数为x,y的方程组 , 其中a与x,y都是正整数,该方程组的解x与y是否具有“邻好关系”?如果具有,请求出a的值及方程组的解;如果不具有,请说明理由.(4)、【拓展】若一个关于x的方程ax+b=0(a≠0)的解为x=b-a,则称之为“成章方程”.如:x+=0的解为x=- , 而-=-1;2x+=0的解为x=- , 而-=-2.若关于x的方程ax+b=0(a≠0)为“成章方程”,请直接写出关于y的方程的解:a(a-b)y+2=(b+)y.
24. 【学习新知】射到平面镜上的光线入射光线和反射后的光线反射光线与平面镜所夹的角相等,如图1,是平面镜,若入射光线与水平镜面夹角为 , 反射光线与水平镜面夹角为 , 则 .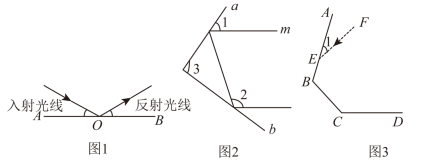 (1)、【初步应用】如图,一束光线射到平面镜上,被反射到平面镜上,又被反射,若被反射出的光线与光线平行,且 , 则 , ;(2)、【猜想验证】由(1),请你猜想:当两平面镜、的夹角 ▲ 时,可以使任何射到平面镜上的光线 , 经过平面镜、的两次反射后,入射光线与反射光线平行,请说明理由;(3)、【拓展探究】如图 , 有三块平面镜 , , , 入射光线与镜面的夹角 , 镜面、的夹角 , 已知入射光线从镜面开始反射,经过为正整数,次反射,当第次反射光线与入射光线平行时,请直接写出的度数.可用含有的代数式表示)
(1)、【初步应用】如图,一束光线射到平面镜上,被反射到平面镜上,又被反射,若被反射出的光线与光线平行,且 , 则 , ;(2)、【猜想验证】由(1),请你猜想:当两平面镜、的夹角 ▲ 时,可以使任何射到平面镜上的光线 , 经过平面镜、的两次反射后,入射光线与反射光线平行,请说明理由;(3)、【拓展探究】如图 , 有三块平面镜 , , , 入射光线与镜面的夹角 , 镜面、的夹角 , 已知入射光线从镜面开始反射,经过为正整数,次反射,当第次反射光线与入射光线平行时,请直接写出的度数.可用含有的代数式表示)