北师大版数学八年级下册单元清测试(第六章)培优卷
试卷更新日期:2024-04-16 类型:单元试卷
一、选择题(每题3分,共30分)
-
1. 如图,在▱ABCD中,已知AB=12,AD=8,∠ABC的平分线BM交CD边于点M,则DM的长为( )
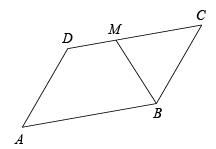 A、2 B、4 C、6 D、82. 如图,在 中, 的平分线交 于点 , 的平分线交 于点 ,若 ,则 的长是( )
A、2 B、4 C、6 D、82. 如图,在 中, 的平分线交 于点 , 的平分线交 于点 ,若 ,则 的长是( ) A、1 B、2 C、2.5 D、33. 如图,点O是 对角线的交点,EF过点O分別交AD,BC于点E,F.下列结论成立的是( )
A、1 B、2 C、2.5 D、33. 如图,点O是 对角线的交点,EF过点O分別交AD,BC于点E,F.下列结论成立的是( )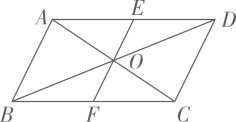 A、 B、 C、 D、4. 如图,在四边形中, , 若添加一个条件,使四边形为平形四边形,则下列正确的是( )
A、 B、 C、 D、4. 如图,在四边形中, , 若添加一个条件,使四边形为平形四边形,则下列正确的是( )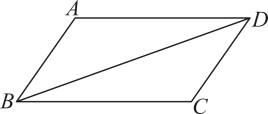 A、 B、 C、 D、5. 如图,在四边形ABCD中,BC∥AD,添加下列条件,不能判定四边形ABCD是平行四边形的是( )
A、 B、 C、 D、5. 如图,在四边形ABCD中,BC∥AD,添加下列条件,不能判定四边形ABCD是平行四边形的是( ) A、AB=CD B、AB∥CD C、∠A=∠C D、BC=AD6. 如图,剪两张对边平行的纸条,随意交叉叠放在一起,重合部分构成一个四边形 , 其中一张纸条在转动过程中,下列结论一定成立的是( )
A、AB=CD B、AB∥CD C、∠A=∠C D、BC=AD6. 如图,剪两张对边平行的纸条,随意交叉叠放在一起,重合部分构成一个四边形 , 其中一张纸条在转动过程中,下列结论一定成立的是( )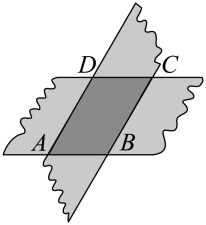 A、四边形周长不变 B、 C、四边形面积不变 D、7. 如图,在中, , 是上的点,交于点 , 交于点 , 那么四边形的周长是( )
A、四边形周长不变 B、 C、四边形面积不变 D、7. 如图,在中, , 是上的点,交于点 , 交于点 , 那么四边形的周长是( )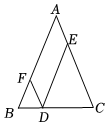 A、5 B、10 C、15 D、208. 如图, 是 边 延长线上一点,连接 , , , 交 于点 .添加以下条件,不能判定四边形 BDEC 为平行四边形的是( )
A、5 B、10 C、15 D、208. 如图, 是 边 延长线上一点,连接 , , , 交 于点 .添加以下条件,不能判定四边形 BDEC 为平行四边形的是( )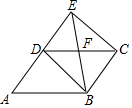 A、 B、 C、 D、9. ▱ABCD中,E,F是对角线BD上不同的两点,下列条件中,不能得出四边形AECF一定为平行四边形的是( )
A、 B、 C、 D、9. ▱ABCD中,E,F是对角线BD上不同的两点,下列条件中,不能得出四边形AECF一定为平行四边形的是( )
A、BE=DF B、AE=CF C、AF//CE D、∠BAE=∠DCF10. 如图,在中, , , 是边的中点,是边上一点,若平分的周长,则的长为( )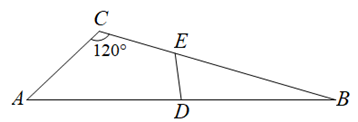 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每题3分,共18分)
-
11. 如图,在平行四边形中, , , 的平分线交于点E,则的长为 .
 12. 如图,在中,为的中点,过点且分别交于点 . 若 , 则的长为 .
12. 如图,在中,为的中点,过点且分别交于点 . 若 , 则的长为 .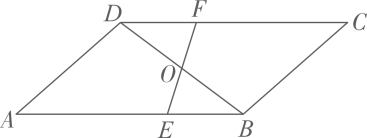 13. 如图,小宇将一张平行四边形纸片折叠,使点落在长边上的点处,并得到折痕 , 小宇测得长边 , 则四边形的周长为 .
13. 如图,小宇将一张平行四边形纸片折叠,使点落在长边上的点处,并得到折痕 , 小宇测得长边 , 则四边形的周长为 . 14. 如图,点E,F分别在▱ABCD的边AB,CD的延长线上,连接EF,分别交AD,BC于G,H.添加一个条件使△AEG≌△CFH,这个条件可以是.(只需写一种情况)
14. 如图,点E,F分别在▱ABCD的边AB,CD的延长线上,连接EF,分别交AD,BC于G,H.添加一个条件使△AEG≌△CFH,这个条件可以是.(只需写一种情况)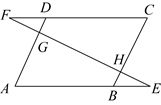 15. 如图所示,已知 , 正五边形的顶点、在射线上,顶点在射线上,则度.
15. 如图所示,已知 , 正五边形的顶点、在射线上,顶点在射线上,则度.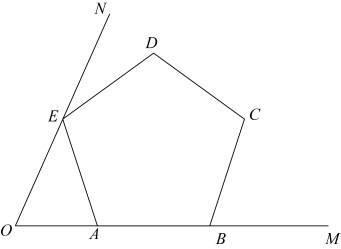 16. 如图,将 沿对角线 翻折,点 落在点 处, 交 于点 ,若 , , , ,则 的周长为 .
16. 如图,将 沿对角线 翻折,点 落在点 处, 交 于点 ,若 , , , ,则 的周长为 .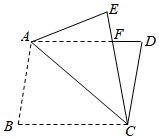
三、解答题(共8题,共72分)
-
17. 如图,在中, , 分别是边和上的点,连接 , , 且 . 求证:
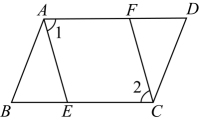 (1)、;(2)、 .18. 如图,B是AC的中点,点D,E在同侧, , .
(1)、;(2)、 .18. 如图,B是AC的中点,点D,E在同侧, , .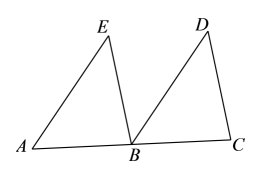 (1)、求证:≌ .(2)、连接 , 求证:四边形是平行四边形.19. 已知:如图,点为对角线的中点,过点的直线与 , 分别相交于点 , .
(1)、求证:≌ .(2)、连接 , 求证:四边形是平行四边形.19. 已知:如图,点为对角线的中点,过点的直线与 , 分别相交于点 , .求证: .
 20. 如图,▱ABCD的对角线AC,BD相交于点O,点E,F在AC上,且AE=CF.
20. 如图,▱ABCD的对角线AC,BD相交于点O,点E,F在AC上,且AE=CF. (1)、求证:BE∥DF;(2)、过点O作OM⊥BD,垂足为O,交DF于点M,若△BFM的周长为12,求四边形BEDF的周长.21. 如图,中,点D、E分别为的中点,延长到点F,使得 , 连接 . 求证:
(1)、求证:BE∥DF;(2)、过点O作OM⊥BD,垂足为O,交DF于点M,若△BFM的周长为12,求四边形BEDF的周长.21. 如图,中,点D、E分别为的中点,延长到点F,使得 , 连接 . 求证: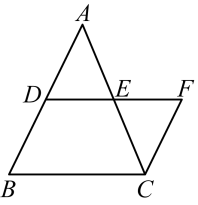 (1)、;(2)、四边形是平行四边形.22. 如图所示,在中,点D、E分别为的中点,点H在线段上,连接 , 点G、F分别为的中点.
(1)、;(2)、四边形是平行四边形.22. 如图所示,在中,点D、E分别为的中点,点H在线段上,连接 , 点G、F分别为的中点. (1)、求证:四边形为平行四边形(2)、 , 求线段的长度.23. 如图
(1)、求证:四边形为平行四边形(2)、 , 求线段的长度.23. 如图
 (1)、如图1,在▱ABCD中,AE平分∠BAD交CD边于点E,已知AB=5cm,AD=3cm,则EC等于cm。(2)、如图2,在▱ABCD中,若AE,BE分别是∠DAB,∠CBA的平分线,点E在DC边上,且AB=4,则ABCD的周长为。(3)、如图3,已知四边形ABCD是平行四边形,AD=BC,若AF,BE分别是∠DAB,∠CBA的平分线。求证:DF=EC(4)、在(3)的条件下,如果AD=3,AB=5,则EF的长为。24.(1)、用数学的眼光观察.
(1)、如图1,在▱ABCD中,AE平分∠BAD交CD边于点E,已知AB=5cm,AD=3cm,则EC等于cm。(2)、如图2,在▱ABCD中,若AE,BE分别是∠DAB,∠CBA的平分线,点E在DC边上,且AB=4,则ABCD的周长为。(3)、如图3,已知四边形ABCD是平行四边形,AD=BC,若AF,BE分别是∠DAB,∠CBA的平分线。求证:DF=EC(4)、在(3)的条件下,如果AD=3,AB=5,则EF的长为。24.(1)、用数学的眼光观察.如图,在四边形中, , 是对角线的中点,是的中点,是的中点,求证: .
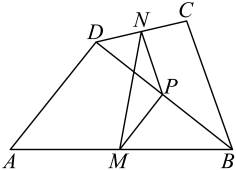 (2)、用数学的思维思考.
(2)、用数学的思维思考.如图,延长图中的线段交的延长线于点 , 延长线段交的延长线于点 , 求证: .
 (3)、用数学的语言表达.
(3)、用数学的语言表达.如图,在中, , 点在上, , 是的中点,是的中点,连接并延长,与的延长线交于点 , 连接 , 若 , 试判断的形状,并进行证明.
