2024年浙教版数学七年级下册期中仿真模拟卷(二)(范围:1-3章)
试卷更新日期:2024-04-16 类型:期中考试
一、选择题(每题3分,共30分)
-
1. 下列运算正确的是A、 B、 C、 D、2. 下列说法正确的是( )A、两点之间,直线最短 B、不相交的两条直线叫做平行线 C、在同一平面内,过一点有且只有一条直线与已知直线垂直 D、直线外一点到这条直线的垂线段叫做点到直线的距离3. 如图,直线的顶点B , C分别在上,若 , 则的大小为( )
 A、 B、 C、 D、4. 二元一次方程组的解为 ( )A、 B、 C、 D、5. 若与的两边分別平行,且 , 则的度数为( )A、 B、 C、或 D、或6. 如图,将一张长方形纸对折两次,产生的折痕与折痕之间的位置关系是( )
A、 B、 C、 D、4. 二元一次方程组的解为 ( )A、 B、 C、 D、5. 若与的两边分別平行,且 , 则的度数为( )A、 B、 C、或 D、或6. 如图,将一张长方形纸对折两次,产生的折痕与折痕之间的位置关系是( )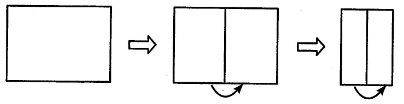 A、平行 B、垂直 C、平行或垂直 D、无法确定7. 如图,将一张长方形纸片沿 EF折叠后,使得点 A,B 分别落在点A',B'的位置,如果∠2=56°,那么∠1=( )
A、平行 B、垂直 C、平行或垂直 D、无法确定7. 如图,将一张长方形纸片沿 EF折叠后,使得点 A,B 分别落在点A',B'的位置,如果∠2=56°,那么∠1=( )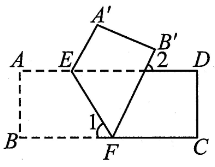 A、56° B、58° C、62° D、68°8. 甲、乙两种商品原来每件的售价和为100元,因市场变化,甲商品降价10%,乙商品提价40%,调价后两种商品的售价和比原来的售价和提高了20%.若设甲、乙两种商品原来每件的售价分别为x元、y元,则下列方程组正确的是( )A、 B、 C、 D、9. 如图,已知长方形纸片 ABCD,点E,F分别在边AD和BC上,且∠EFC=53°,H和G 分别是边AD和 BC 上的动点,现将点 A,B 沿 EF 向下折叠至点N,M 处,将点 C,D沿GH 向上折叠至点P,K 处,若 MN∥PK,则∠KHD的度数为 ( )
A、56° B、58° C、62° D、68°8. 甲、乙两种商品原来每件的售价和为100元,因市场变化,甲商品降价10%,乙商品提价40%,调价后两种商品的售价和比原来的售价和提高了20%.若设甲、乙两种商品原来每件的售价分别为x元、y元,则下列方程组正确的是( )A、 B、 C、 D、9. 如图,已知长方形纸片 ABCD,点E,F分别在边AD和BC上,且∠EFC=53°,H和G 分别是边AD和 BC 上的动点,现将点 A,B 沿 EF 向下折叠至点N,M 处,将点 C,D沿GH 向上折叠至点P,K 处,若 MN∥PK,则∠KHD的度数为 ( )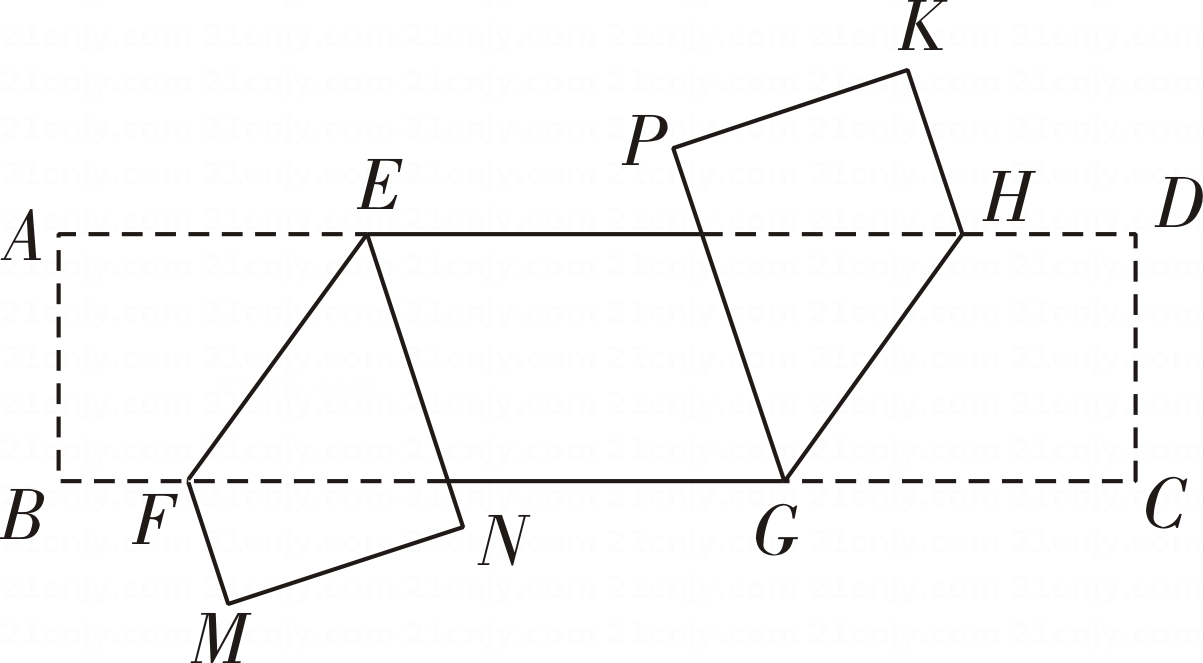 A、37°或143° B、74°或96° C、37°或105° D、74°或106°10. 如图1,当光从空气进入水中时,会发生折射,满足入射角∠1 与折射角∠2 的度数比为4:3.如图2,在同一平面上,两条光线同时从空气进入水中,两条入射光线与水面的夹角分别为α,β,水中两条折射光线的夹角为γ,则α,β,γ三者之间的数量关系为( )
A、37°或143° B、74°或96° C、37°或105° D、74°或106°10. 如图1,当光从空气进入水中时,会发生折射,满足入射角∠1 与折射角∠2 的度数比为4:3.如图2,在同一平面上,两条光线同时从空气进入水中,两条入射光线与水面的夹角分别为α,β,水中两条折射光线的夹角为γ,则α,β,γ三者之间的数量关系为( )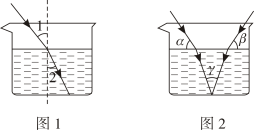 A、 B、 C、α+β=γ D、
A、 B、 C、α+β=γ D、二、填空题(每题3分,共18分)
-
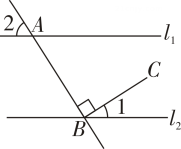
11. 已知 , 用含的代数式表示 , 则.12. a,b,c为同一平面内三条不同的直线,若a⊥b,c⊥b,则a与c的位置关系是.13. 已知是二元一次方程组的解,则m-n= .14. 如图,l1∥l2 , 直线AB截l1于点A,截l2于点B,BC⊥AB,若∠1=30°,则∠2=°
 15. 图1,由两个相同的小长方形组成的图形周长为10,图2中在长方形ABCD内放置了若干个相同的小长方形,则长方形ABCD的周长为.
15. 图1,由两个相同的小长方形组成的图形周长为10,图2中在长方形ABCD内放置了若干个相同的小长方形,则长方形ABCD的周长为.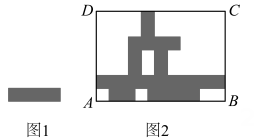 16. 如图1是一张长方形纸带,∠DEF=20°,若将纸带沿EF折叠成图2,再沿BF折叠成图3,则图3中的∠CFE的度数为°.
16. 如图1是一张长方形纸带,∠DEF=20°,若将纸带沿EF折叠成图2,再沿BF折叠成图3,则图3中的∠CFE的度数为°.
三、解答题(共8题,共72分)
-
17. 计算:(1)、;(2)、.18. 解方程组:(1)、(2)、19. 已知:如图, , , 试说明:(请按图填空,并补充理由):

证明:(已知),
▲ ▲ , ( )
, (两直线平行,内错角相等)
又(已知)
▲ , (等量代换)
▲ ▲ , (内错角相等,两直线平行)
. ( )
20. 已知关于x,y的方程组.(1)、若方程组的解满足 , 求的值;(2)、当取不同实数时,的值是否发生变化,如果不变,求出的值,如果改变,请说明理由。(3)、x,y的自然数解是.21. 如图,已知∠1=∠BDC,∠2+∠3=180°. (1)、AD与EC 平行吗? 试说明理由。(2)、若 DA平分∠BDC,CE⊥AE,∠1=80°,试求∠FAB的度数。22. 如图1,我们在某月的日历中标出一个十字星,并计算它的“十字差”(先将十字星左右两数,上下两数分别相乘,再将所得的积作差,即为该十字星的“十字差”),则该十字星的“十字差”为12×14-6×20=48,再选择其他位置的十字星,可以发现“十字差”仍为48.
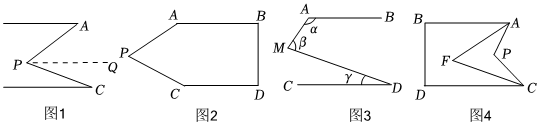
(1)、AD与EC 平行吗? 试说明理由。(2)、若 DA平分∠BDC,CE⊥AE,∠1=80°,试求∠FAB的度数。22. 如图1,我们在某月的日历中标出一个十字星,并计算它的“十字差”(先将十字星左右两数,上下两数分别相乘,再将所得的积作差,即为该十字星的“十字差”),则该十字星的“十字差”为12×14-6×20=48,再选择其他位置的十字星,可以发现“十字差”仍为48.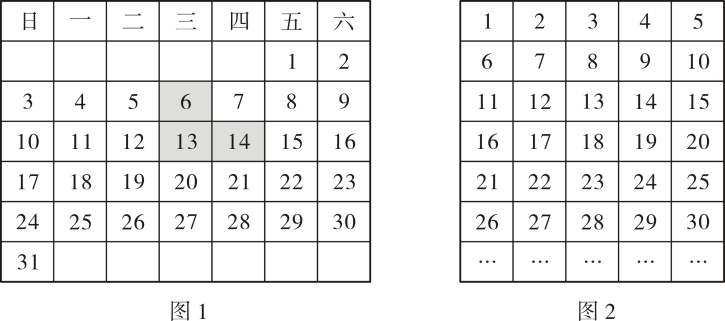 (1)、如图2,将正整数依次填入5列的长方形数表中,探究不同位置十字星的“十字差”,可以发现相应的“十字差”也是 一个定值,这个定值为.(2)、若将正整数依次填入6列的长方形数表中,不同位置十字星的“十字差”是一个定值吗? 如果是,请求出这个定值;如果不是,请说明理由.(3)、若将正整数依次填入k列的长方形数表中(k≥3),继续前面的探究,可以发现相应的“十字差”只与列数k有关,请用含 k的代数式表示出这个“十字差”,并说明理由.23. 定义:任意两个数 , , 按规则运算得到一个新数 , 称所得的新数为 , 的“和积数”.(1)、若 , , 求 , 的“和积数”;(2)、若 , , 求 , 的“和积数”;(3)、已知 , 且 , 的“和积数” , 求用含的式子表示并计算的最小值.24. 探索发现:如图是一种网红弹弓的实物图,在两头上系上皮筋,拉动皮筋可形成平面示意图如图图 , 弹弓的两边可看成是平行的,即各活动小组探索与 , 之间的数量关系已知 , 点不在直线和直线上,在图中,智慧小组发现:智慧小组是这样思考的:过点作 , .
(1)、如图2,将正整数依次填入5列的长方形数表中,探究不同位置十字星的“十字差”,可以发现相应的“十字差”也是 一个定值,这个定值为.(2)、若将正整数依次填入6列的长方形数表中,不同位置十字星的“十字差”是一个定值吗? 如果是,请求出这个定值;如果不是,请说明理由.(3)、若将正整数依次填入k列的长方形数表中(k≥3),继续前面的探究,可以发现相应的“十字差”只与列数k有关,请用含 k的代数式表示出这个“十字差”,并说明理由.23. 定义:任意两个数 , , 按规则运算得到一个新数 , 称所得的新数为 , 的“和积数”.(1)、若 , , 求 , 的“和积数”;(2)、若 , , 求 , 的“和积数”;(3)、已知 , 且 , 的“和积数” , 求用含的式子表示并计算的最小值.24. 探索发现:如图是一种网红弹弓的实物图,在两头上系上皮筋,拉动皮筋可形成平面示意图如图图 , 弹弓的两边可看成是平行的,即各活动小组探索与 , 之间的数量关系已知 , 点不在直线和直线上,在图中,智慧小组发现:智慧小组是这样思考的:过点作 , .
 (1)、填空:过点作 .
(1)、填空:过点作 .
所以 ,
因为 , ,
所以 ▲ ,
所以 ,
所以 ,
即 .(2)、在图中,猜测与 , 之间的数量关系,并完成证明.(3)、善思小组提出:
如图 , 已知 , 则角、、之间的数量关系为 ▲ 直接填空
如图 , , , 分别平分 , 则与之间的数量关系为 ▲ 直接填空